机器人运动规划中的构形空间（Configuration Space）

　　A key concept in motion planning is configuration space, or C-space for short. Every point in the C-space C corresponds to a unique configuration q of the robot, and every configuration of the robot can be represented as a point in C-space. This description is convenient because it allows us to describe the complex 3D shape of the robot with a single n-dimensional point. For example, the configuration of a robot arm with n joints can be represented as a list of n joint positions, q = (θ₁, . . . , θ_n). The free C-space C_free consists of the configurations where the robot neither penetrates an obstaclen or violates a joint limit. 

　　The workspace obstacles partition the configuration space C into two sets, the free space C_free and the obstacle space C_obs, where C = C_free ∪ C_obs. Joint limits are treated as obstacles in the configuration space. With the concepts of C_free and C_obs, the path planning problem reduces to the problem of finding a path for a point robot among the obstacles C_obs. If the obstacles break C_free into separate connected components, and q_start and q_goal do not lie in the same connected component, then there is no collision-free path. The goal of path planning is to find a path in the work space from the initial position to the goal position, avoiding all collisions with the obstacles. This is a difficult problem to visualize and solve in the physical space, particularly as dimension grows large. But in configuration space the problem is straightforward.

 　　一般移动机器人的路径规划问题都将其假设为一个点，忽略外形以及尺寸来简化问题。但在实际控制机器人时就必须考虑其真实尺寸，这时机器人就不能被简单地当做一个点。

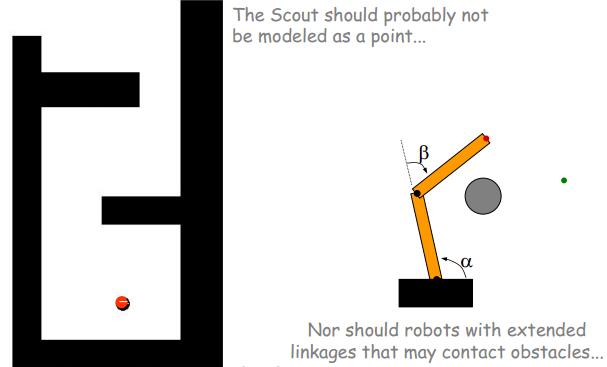
What if the robot is not a point? 

 

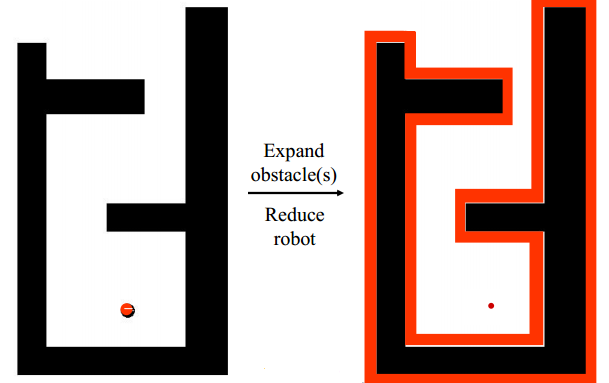
　　对平面机器人来说，C-Space就是以机器人的尺寸为基础，对工作空间进行一定的膨胀即可得到：

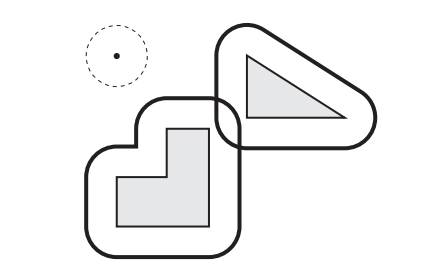
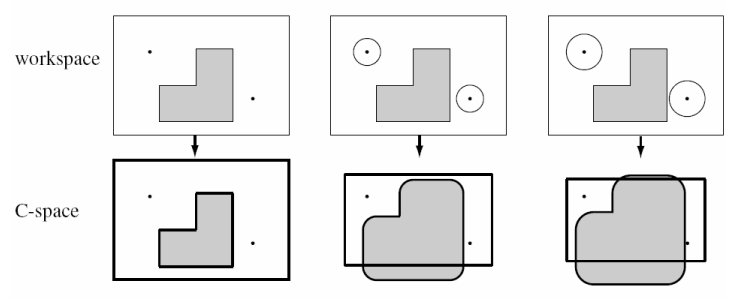
　　如果对工作空间中的障碍物进行膨胀产生了重叠的部分，如下图所示，则表示机器人不能通过那个区域：

　　C-Space与机器人实际形状和尺寸有关，从下图可以看出中间和右边两个机器人由于尺寸（直径）太大而不能通过工作空间的某些区域：

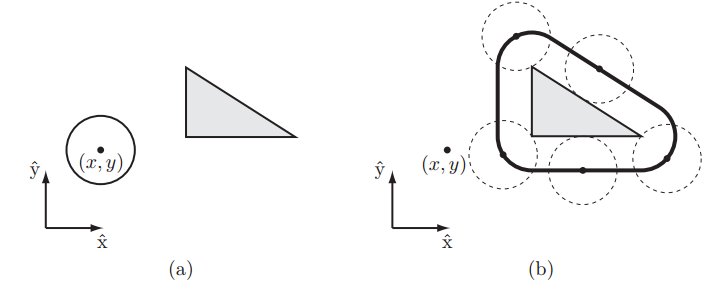
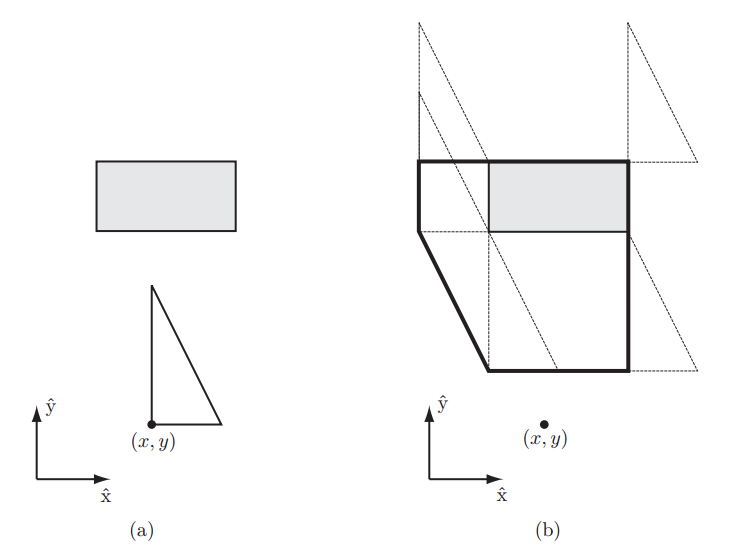
　　另外机器人的形状也会影响C-Space。下图中的直角三角形代表一个三角形状的机器人，只能在平面内平移，其参考位置点在图中的(x,y)处。灰色矩形是工作空间内的障碍物，将机器人贴着障碍物边界滑行一圈，追踪参考点的位置可以画出一个黑色粗线框的多边形区域。这个区域就是该三角形机器人C-Space中的障碍区域。

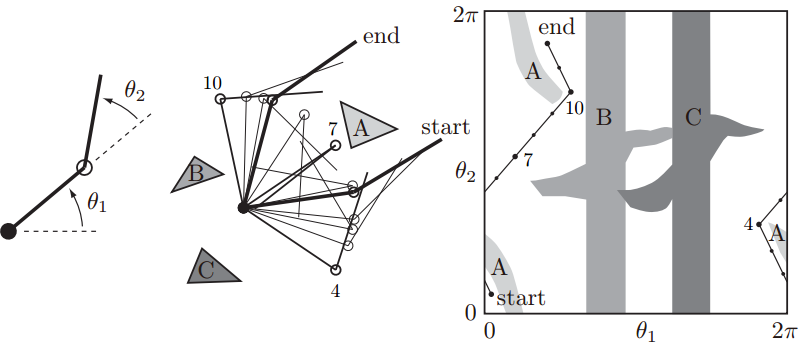
 　　下面是一个关节型机器人的例子。平面二连杆机器人有两个自由度，可以绕两个关节分别旋转0-360°，中间的图描绘了在工作空间中机器人从初始位置开始经过一系列中间点避开障碍物A、B、C运动到目标位置。右图是与之对应的C-Space中的情形：

 　　注意θ₁ = 0和θ₁ = 2π（θ₂ = 0和θ₂ = 2π）其实是一个角度，因此上面C-Space的左右边界和上下边界其实是连在一起的。其拓扑结构是一个圆环面（torus），正方形构型空间可从圆环面的θ₁ = 0、θ₂ = 0处切开、展平得到。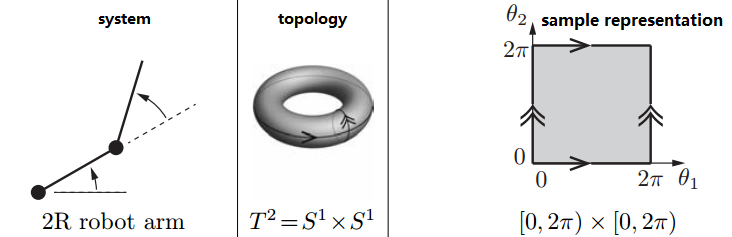

 　　任何落在C-obstacle中的点都表示位于该构型时机械臂与障碍物发生了碰撞。C-Space中从start到end的路径代表了一条工作空间中无碰撞的路径。注意障碍物将C_free分隔成了三个连通区域（connected components
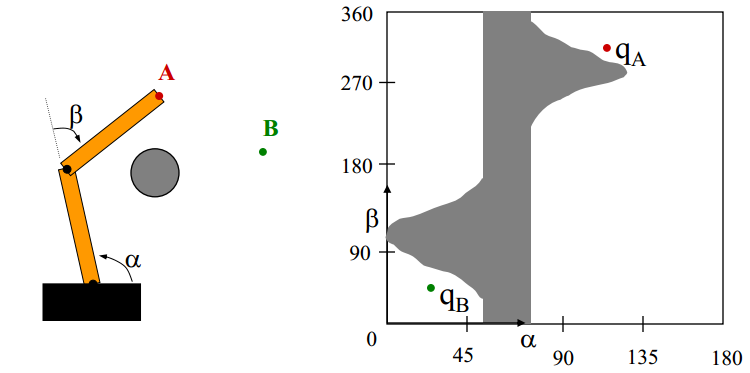
），且起点和终点处于同一连通区域中。然而下图这种情况，起始状态q_A和目标状态q_B分别位于不连通的区域内，机械臂从A运动到B无论怎么走必然会撞到障碍物。

 

 

 

参考：

Modern Robotics Mechanics, Planning, and Control

Modern Robotics home page

Robotics Modelling, Planning and Control Chapter 12. Motion Planning

Springer Handbook of Robotics  Chapter 5. Motion Planning

Robotic Motion Planning: Configuration Space 

知乎 机器人运动规划中的C space怎样理解？