VTK中模型的旋转与平移
当从外界读入STL等三维模型时，其会按照它内部的坐标位置进行显示。因此它的位置和大小是确定的。但是在实际应用中，有可能需要人为地对这个模型在空间中进行旋转、平移或缩放等操作。VTK中有许多和旋转、平移相关的函数，下面一一进行测试。
- RotateX、RotateY、RotateZ（绕自身坐标轴旋转）
Rotate the Prop3D in degrees about the X/Y/Z axis using the right hand rule. The axis is the Prop3D's X/Y/Z axis, which can change as other rotations are performed. 即前一次的旋转会影响到后一次。
假设物体坐标系开始与世界坐标系重合，先后调用RotateZ(90)、RotateX(90)的结果如下图所示：
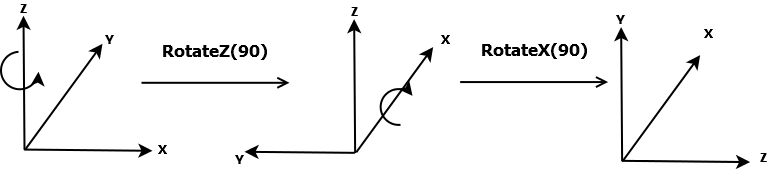
使用GetOrientation可以获取当前物体的姿态信息，结果为(90, 0, 90)。GetOrientation：Returns the orientation of the Prop3D as s vector of X,Y and Z rotation. The ordering in which these rotations must be done to generate the same matrix is RotateZ, RotateX, and finally RotateY. 即按照Z-X-Y的顺序将世界坐标系绕自身旋转即可得到当前姿态。
- RotateWXYZ（绕世界坐标系旋转）
Rotate the Prop3D in degrees about an arbitrary axis specified by the last three arguments. The axis is specified in world coordinates. 该函数的后三个参数指定旋转方向（可以是任意方向，不一定非得是坐标轴方向）。如按世界坐标系的X轴旋转可写为RotateWXYZ(deg, 1, 0, 0)，按世界坐标系的Z轴旋转可写为RotateWXYZ(deg, 0, 0, 1)。同样是先后调用RotateWXYZ(90,0,0,1)、RotateWXYZ(90,1,0,0)得到的结果如下：
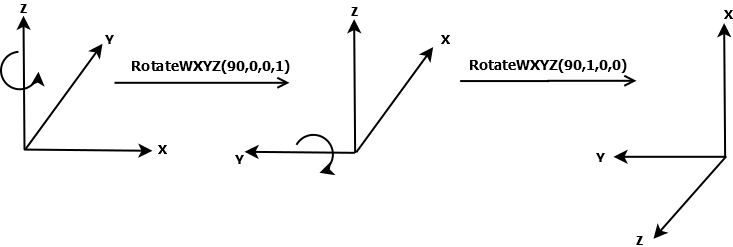
此时调用GetOrientation返回值是：(0, -90, 90)，即将世界坐标系先绕自身Z轴旋转90°，再绕X轴旋转0°，最后绕Y轴旋转-90°即可到达当前姿态。
- SetOrientation(x, y, z) —— 通过先绕Z轴，然后绕X轴，最后绕Y轴旋转，从而来确定Prop的方向。
- AddOrientation(a1, a2,a3) —— 在当前Prop方向增加a1, a2, a3增量。
- SetOrigin（设置旋转中心点）
Set the origin of the Prop3D. This is the point about which all rotations take place. 调用RotateX或RotateWXYZ等旋转函数时会默认旋转中心在原点，即会绕着(0, 0, 0)沿着某一方向旋转。通过调用SetOrigin函数可以改变旋转点的位置。例如一个长宽高都是100的立方体，绕自身Z轴旋转45°，下图左边是默认旋转中心在原点，右边是调用SetOrigin设置旋转中心在(50,0,0)的结果
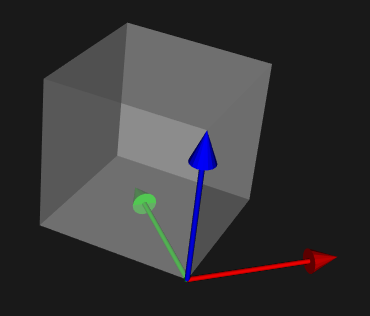
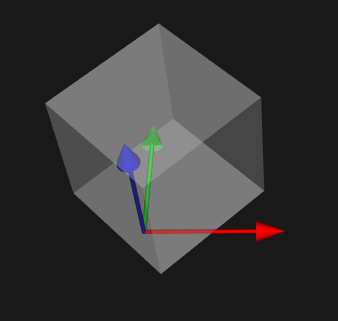
- SetPosition、AddPosition（设置物体在世界坐标系中的位置）
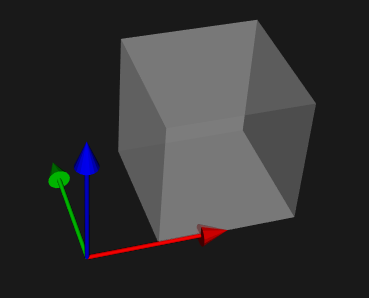
SetPosition(x, y, z)—— 指定vtkProp3D对象在世界坐标系中的位置。AddPosition(deltaX, deltaY, deltaZ) —— 用指定的X、Y、Z三个方向的增量来平移Prop。如下图中立方体开始在原点处，调用SetPosition(50,0,0)后其位置变为(50,0,0)。可以通过GetPosition函数查看物体在世界坐标系中的位置。
- SetUserTransform、GetUserTransform
The most important aspect to applying transformation matrices is to understand the order in which the transformations are applied. Most of the methods for manipulating this transformation, e.g. Translate, Rotate, and Concatenate, can operate in either PreMultiply (the default) or PostMultiply mode. In PreMultiply mode, the translation, concatenation, etc. will occur before any transformations which are represented by the current matrix. In PostMultiply mode, the additional transformation will occur after any transformations represented by the current matrix.
进行变换时的顺序非常重要，对于变换矩阵VTK里是用以下的顺序来应用这些变换的：
$$T_T=T(p_x+o_x,p_y+o_y,p_z+o_z)\cdot R_Z\cdot R_X\cdot R_Y\cdot S(s_x,s_y,s_z)\cdot T(-o_x,-o_y,-o_z)$$
1. 移动Prop到原点；
2. 缩放；
3. 绕Y轴旋转；
4. 绕X轴旋转；
5. 绕Z轴旋转；
6. 从原点中移动回原来的位置；
7. 平移。
因为默认是进行左乘所以进行变换时先调用的最后才变换（即逆序），下面的代码实现了公式中的变换：
vtkTransform *myTrans = vtkTransform::New ();
myTrans->Translate (position[0],position[1],position[2]);
myTrans->Translate (origin[0],origin[1],origin[2]);
myTrans->RotateZ (orientation[2]);
myTrans->RotateX (orientation[0]);
myTrans->RotateZ (orientation[1];
myTrans->Scale (scale[0],scale[1],scale[2]);
myTrans->Translate (-origin[0],-origin[1],-origin[2]);
actor->SetUserTransform(myTrans);
vtkTransform::PreMultiply()用于设置左乘. Sets the internal state of the transform to PreMultiply. All subsequent operations will occur before those already represented in the current transformation. In homogeneous matrix notation, M = M*A where M is the current transformation matrix and A is the applied matrix. The default is PreMultiply.
vtkTransform::PostMultiply()用于设置右乘，Sets the internal state of the transform to PostMultiply. M = A*M where M is the current transformation matrix and A is the applied matrix.
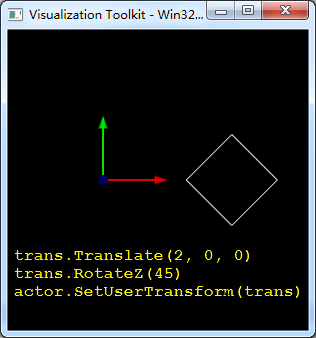
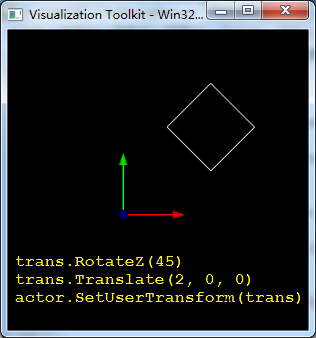
如下所示，左边平面先旋转45°再沿X轴正方向移动2个单位；右边平面先沿X轴正方向移动2个单位，然后旋转45°（旋转中心在原点）。可以看出函数调用顺序颠倒一下产生了截然不同的两种结果（We always specify transformations in the reverse order of their application）
- SetUserMatrix、GetUserMatrix
The UserMatrix can be used in place of UserTransform. Transformation matrices can be combined by matrix multiplication to achieve combinations of translation, rotation, and scaling. It is possible for a single transformation matrix to represent all types of transformation simultaneously.
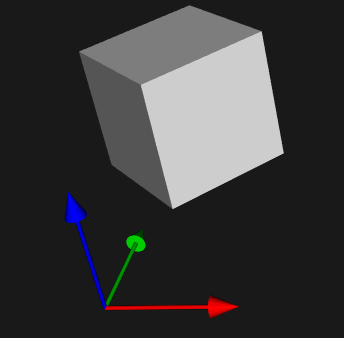
下面代码将物体绕Z轴旋转45°，并移动到(50, 50, 50)处
trans = [0.707107, -0.707107, 0, 50, 0.707107, 0.707107, 0, 50, 0, 0, 1, 50, 0, 0, 0, 1] mat = vtk.vtkMatrix4x4() mat.DeepCopy(trans) actor.SetUserMatrix(mat)
- GetMatrix
UserMatrix is one you can assign yourself to an actor or a top-level composite assembly of actors. Matrix is computed automatically from any position, rotation or scale the actor may have, in addition to the UserMatrix. Calling GetMatrix should always give you the exact matrix applied to an actor to get it to from whatever its own "model space" is to VTK world space. UserMatrix is nullptr until you set it, or until the actor is added as part of an assembly, where the parent assembly may set user matrices directly for its constituent parts. You can't set the matrix directly, but you can set the UserMatrix directly.
GetMatrix与GetUserMatrix函数有很大区别：GetUserMatrix用来获取用户设置的变换矩阵，如果用户没有设置则会返回空，而GetMatrix则始终都会返回场景中物体相对世界坐标系的变换矩阵。
import vtk # create a rendering window and renderer ren = vtk.vtkRenderer() renWin = vtk.vtkRenderWindow() renWin.AddRenderer(ren) # create a renderwindowinteractor iren = vtk.vtkRenderWindowInteractor() iren.SetRenderWindow(renWin) # create plane source plane = vtk.vtkPlaneSource() plane.SetXResolution(1) plane.SetYResolution(1) plane.SetCenter(0,0,0) plane.SetNormal(0,0,1) # mapper mapper = vtk.vtkPolyDataMapper() mapper.SetInputConnection(plane.GetOutputPort()) # actor actor = vtk.vtkActor() actor.SetMapper(mapper) actor.GetProperty().SetRepresentationToWireframe() # assign actor to the renderer ren.AddActor(actor) # create coordinate axes in the render window axes = vtk.vtkAxesActor() axes.SetTotalLength(1, 1, 1) axes.SetShaftType(0) axes.SetAxisLabels(0) axes.SetCylinderRadius(0.02) ren.AddActor(axes) style = vtk.vtkInteractorStyleTrackballCamera() style.SetDefaultRenderer(ren) iren.SetInteractorStyle(style) actor.RotateZ(45) actor.SetPosition(2,0,0) print actor.GetMatrix() print actor.GetUserMatrix() print actor.GetUserTransform () print '---------------------------' trans = vtk.vtkTransform() trans.RotateZ(-45) trans.Translate(-2, 0, 0) actor.SetUserTransform(trans) print actor.GetMatrix() print actor.GetUserMatrix() print actor.GetUserTransform () camera = vtk.vtkCamera() camera.ParallelProjectionOn() ren.SetActiveCamera(camera) ren.ResetCamera() # enable user interface interactor iren.Initialize() renWin.Render() iren.Start()
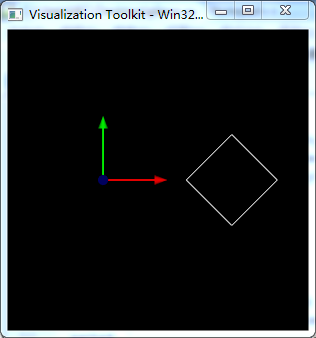
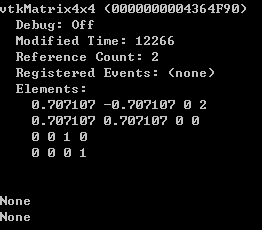
先将平面绕Z轴旋转45°，再移动到(2,0,0)位置，三个函数输出如下图所示。由于没有显式调用SetUserMatrix或SetUserTransform设置UserMatrix，因此GetUserMatrix和GetUserTransform函数返回均为None。
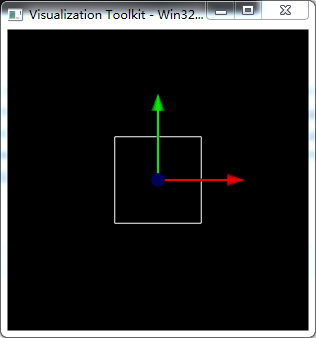
然后将平面沿X轴负方向平移2个单位，再绕Z轴旋转-45°，将平面变换回初始位置（如果想先旋转再平移将其变换回初始位置，则要重新设置旋转中心，否则旋转时会绕原点旋转）。从下图可以看出GetMatrix函数返回了单位矩阵，即现在平面的位置和姿态与世界坐标系一致。GetUerMatrix和GetUserTransform返回的变换矩阵一样：T=Rz(-45°)·T(-2, 0, 0)，为平移和旋转所构成的变换矩阵。
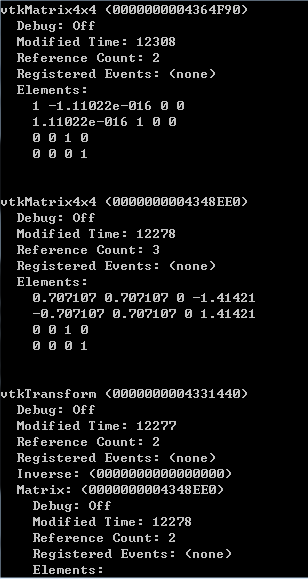
平面由初始位置变换到新位置再变换回去，两次操作互逆，因此变换矩阵互为逆矩阵。
注意：已知B→A的齐次变换矩阵T，则A→B的齐次变换矩阵T-1如下：
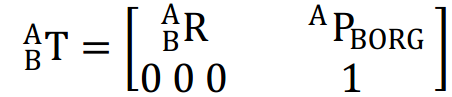
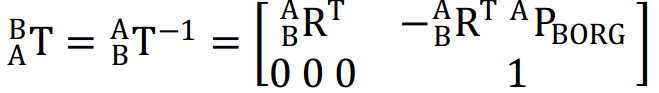
参考：
