OpenModelica仿真
复杂产品通常涉及机械、控制、电子、液压、气动和软件等多学科领域，其设计过程需要进行仿真，以满足对成本、质量、性能等的要求。目前各个学科和领域都已经有了比较成熟的仿真软件，但大部分仿真软件仅适用于本学科领域，并在模型表述中采用自己专门的格式，而复杂产品的整体性能需要多个领域仿真软件的协同仿真，需要在多个仿真软件间进行大量的数据交换，并进行系统层面上的建模，单领域仿真建模工具很难满足要求。Modelica语言就是在这一背景下推出的一种面向对象的非因果关系的仿真建模语言。它的目的是为动态系统建立一种标准的基于方程模型的仿真语言，使得仿真建模与具体的仿真工具分离，实现仿真建模的标准化。
用Modelica语言建模可以采用两种方式，一种是使用图形建模工具，通过拖放模型库中的标准部件、绘制部件间的连接、给出部件的参数，来建立系统的模型组成。另一种方式是用Modelica语言的文本方式。
求解方程时不需考虑信号的传输方向，因此不必像其他仿真软件那样分析模块间的因果关系，大大降低了建模的难度，这与Simulink不同，Simulink本质上是一种赋值运算，由其方框图描述的系统是因果的
下面是一个RLC 电路图，要仿真电阻两端电压随时间变化的暂态过程。
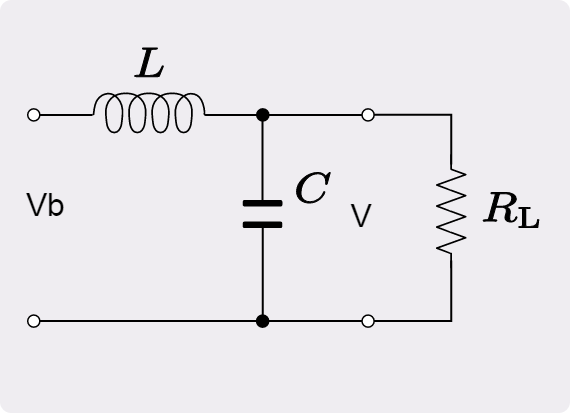
OpenModelica是一个开源的基于Modelica语言的建模和仿真环境，用于工业界和学术界研究。长期由非赢利组织Open Source Modelica Consortium (OSMC) 开发。在OpenModelica中新建一个类，命名为RLC1，在库中选择Electrical/Basic/Analog中的电容、电阻、电感以及大地模块和Source中的恒定电压源模块，将其拖入组件视图中，设定好参数后，将其连接。
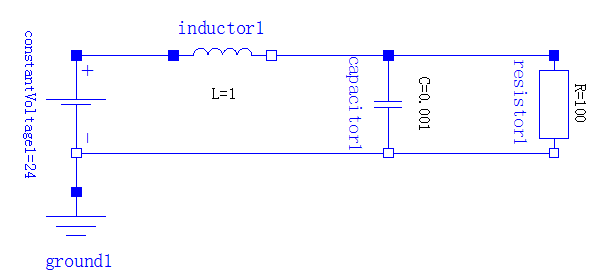
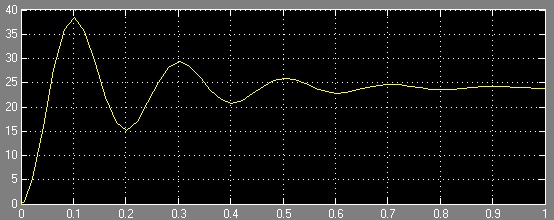
设置仿真时间为1s，然后开始仿真，输出曲线如下图所示。
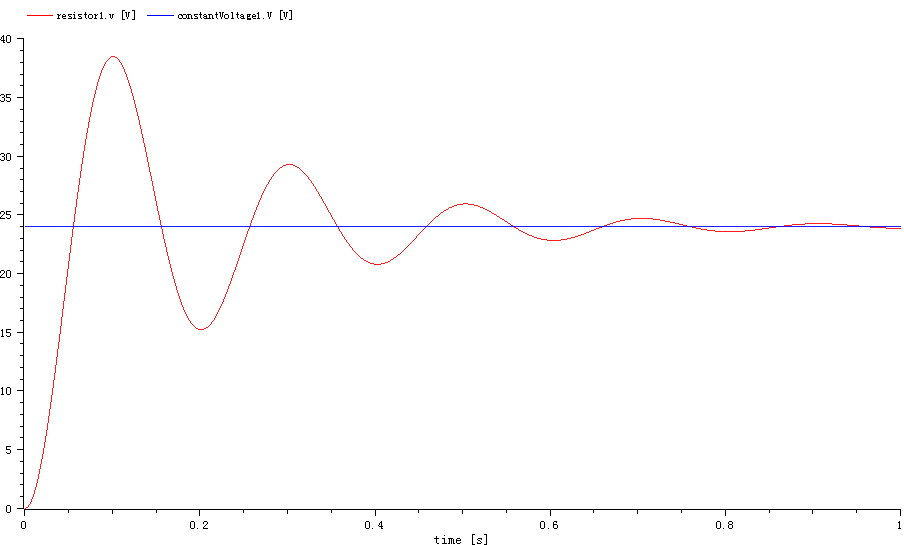
以电阻两端电压Uo作为输出，根据电阻、电容、电感的特性和基尔霍夫电压定律，可以列出系统的2阶微分方程：
$$LC\frac{d^2u_0}{dt^2}+\frac{L}{R} \frac{du_0}{dt}+u_0=u_i$$
则系统传递函数为：
$$\frac{U_o(s)}{U_i(s)}=\frac{1}{LCs^2+\frac{L}{R} s+1}$$
在MATLAB/Simulink中仿真二阶系统的阶跃响应
可以得到相同的结果：
参考：
