离散傅里叶变换（DFT）
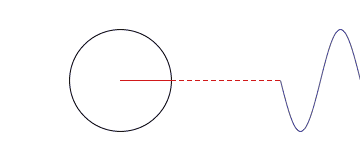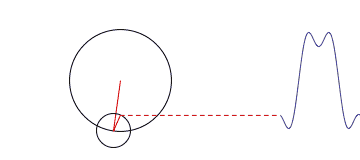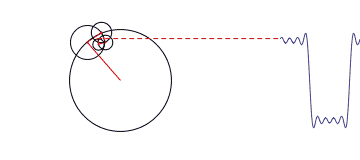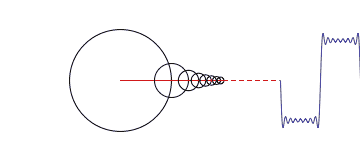
对于第一幅图来说，它侧重展示傅里叶变换的本质之一：叠加性，每个圆代表一个谐波分量。第二幅图直观的表示了一个周期信号在时域与频域的分解。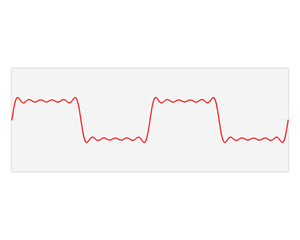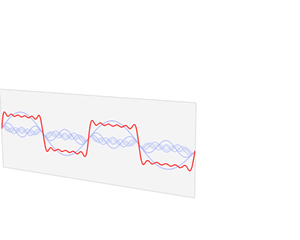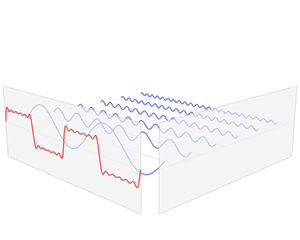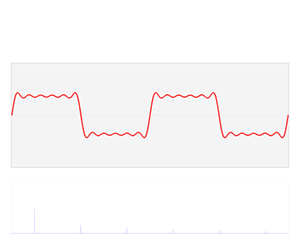
- 周期信号的三角函数表示
周期信号是每隔一定时间间隔，按相同规律无始无终重复变化的信号。任何周期函数在满足狄利克雷条件下（连续或只有有限个间断点，且都是第一类间断点；只有有限个极值点），都可以展开成一组正交函数的无穷级数之和。使用三角函数集的周期函数展开就是傅里叶级数。对于周期为T的信号f(t)，可以用三角函数集的线性组合来表示，即
$$f(t)=a_0+\sum_{n=1}^{\infty }(a_n\cos n\omega t+b_n\sin n \omega t)$$
式中$\omega=\frac{2\pi}{T}$是周期信号的角频率，也成基波频率，$n\omega$称为n次谐波频率；$a_0$为信号的直流分量，$a_n$和$b_n$分别是余弦分量和正弦分量幅度。根据级数理论，傅里叶系数$a_0$、$a_n$、$b_n$的计算公式为：
$$\left\{\begin{matrix}a_0=\frac{1}{T}\int _{\frac{-T}{2}}^{\frac{T}{2}}f(t)dt
\\ a_n=\frac{2}{T}\int _{\frac{-T}{2}}^{\frac{T}{2}}f(t)\cos{n\omega t}dt,n=1,2,3,...
\\ b_n=\frac{2}{T}\int _{\frac{-T}{2}}^{\frac{T}{2}}f(t)\sin{n\omega t}dt,n=1,2,3,...
\end{matrix}\right.$$
若将式子中同频率的正弦项和余弦项合并，得到另一种形式的周期信号的傅里叶级数，即
$$f(t)=A_0+\sum_{n=1}^{\infty}A_n\cos(n\omega t+\varphi_n)$$
其中，$A_0$为信号的直流分量；$A_1\cos(\omega t+\varphi_1)$为信号的基频分量，简称基波；$A_n\cos(n\omega t+\varphi_n)$为信号的n次谐波，n比较大的谐波，称为高次谐波。上式说明任何周期信号只要满足狄利克雷条件，都可以分解成直流分量和一系列谐波分量之和，这些谐波分量的频率是周期信号基频的整数倍。
比较两种三角函数形式的傅里叶级数，可以看出它们的系数有如下关系：
$$\left\{\begin{matrix}A_0=a_0
\\A_n=\sqrt{a_n^2+b_n^2},\quad\varphi_n=-\arctan\frac{b_n}{a_n}
\\a_n=A_n\cos \varphi_n,\quad b_n=A_n\sin\varphi_n
\end{matrix}\right.$$
- 周期信号的复指数表示
利用欧拉公式
$$\cos n\omega t=\frac{e^{jn\omega t}+e^{-jn\omega t}}{2}\quad\quad\sin n\omega t=\frac{e^{jn\omega t}-e^{-jn\omega t}}{2j}$$
可以得到周期信号的复指数形式的傅里叶级数展开，即
$$f(t)=\sum_{n=-\infty}^{\infty}F_ne^{jn\omega t}$$
其中展开系数为
$$F_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\omega t}dt$$
虽然n的取值范围为$(-\infty,\infty)$，但n取负值并不表示实际上存在负频率。周期信号可以用三角函数形式的傅里叶级数表示，也可以用复指数形式的傅里叶级数表示。前者物理意义明确，后者在数学处理上简便，并且容易与傅里叶变换统一起来。
- 周期信号的频谱图
为了方便和直观的表示一个周期信号中所含有的频率分量，常用周期信号各次谐波的分布图形表示，这种图形称为信号的频谱图。频谱图由幅度谱图和相位谱图组成，其中幅度谱图表示各次谐波幅度随频率的变化关系，而相位谱图描述各次谐波的相位与频率的关系。根周期信号展开成傅里叶级数的不同形式，频谱图又分为单边频谱图和双边频谱图。
1. 单边频谱图
根据三角函数形式的傅里叶级数展开式
$$f(t)=A_0+\sum_{n=1}^{\infty}A_n\cos(n\omega t+\varphi_n)$$
作出的$A_n$与$n\omega$的关系称为单边幅度频谱，$\varphi_n$与$n\omega$的关系称为单边相位频谱。
例. 画出信号$f(t)=\frac{4}{\pi}[\sin(\omega_1t)+\frac{1}{3}\sin(3\omega_1t)+\frac{1}{5}\sin(5\omega_1t)+\cdots ]$的单边频谱图。
解：$f(t)=\frac{4}{\pi}[\cos(\omega_1t-\frac{\pi}{2})+\frac{1}{3}\cos(3\omega_1t-\frac{\pi}{2})+\frac{1}{5}\cos(5\omega_1t-\frac{\pi}{2})+\cdots ]$
可知其基波频率为ω1，分别有一、三、五......次谐波分量，则其振幅谱和相位谱分别为：
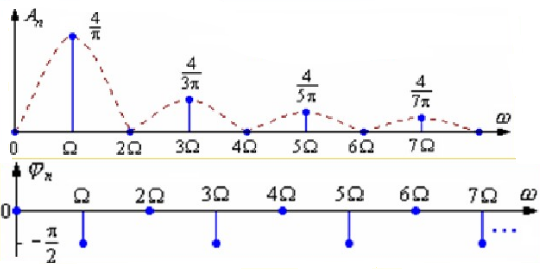
由此可见，周期函数的频谱或谱线只出现在离散点上，分布于整个频域中，形成离散谱，每条谱线间的距离为$\omega_1=\frac{2\pi}{T}$。离散谱是周期函数的重要特征（离散性）。此外，每一条谱线只能出现在基波频率ω1整数倍频率上（谐波性）。各次谐波分量的振幅虽然随着nω1的变化而变，但总的趋势是随着nω1的增大而逐渐减小（收敛性）。
2. 双边频谱图
根据复指数形式的傅里叶级数展开式
$$f(t)=\sum_{n=-\infty}^{\infty}F_ne^{jn\omega t}$$
设$F_n=|F_n|e^{j\varphi_n}$，作出的幅度$|F_n|$与$n\omega$的关系称为双边幅度频谱，相位$\varphi_n$与$n\omega$的关系称为双边相位频谱。
例. 画出信号$f(t)=\frac{4}{\pi}[\sin(\omega_1t)+\frac{1}{3}\sin(3\omega_1t)+\frac{1}{5}\sin(5\omega_1t)+\cdots ]$的双边频谱图。
根据欧拉公式：
$$\sin\beta=\frac{-j}{2}(e^{j\beta}-e^{-j\beta})=\frac{1}{2}(e^{j\beta}e^{-j\frac{\pi}{2}}-e^{-j\beta}e^{j\frac{\pi}{2}})$$
可得：
$$\begin{align*}
F_n=\left\{\begin{matrix}0,\quad &n=0,\pm2,\pm4,\pm6,\cdots
\\ \frac{2}{n\pi}e^{-j\frac{\pi}{2}},\quad &n=1,3,5,7,\cdots
\\ \frac{2}{n\pi}e^{j\frac{\pi}{2}},\quad &n=-1,-3,-5,-7,\cdots
\end{matrix}\right.
\end{align*}$$
则幅值为：$|F_n|=\frac{2}{n\pi}\quad (n\ne0)$，相位为：$\varphi_n=-\frac{\pi}{2}\quad (n>0),\varphi_n=\frac{\pi}{2}\quad (n<0)$
可以看出双边谱在正负频率位置上的幅度为单边幅度谱中对应频率分量幅度的一半。双边谱中负频率出现仅为便于数学运算，没有物理意义，只有将负频率项与相应的正频率项合并，才是实际的频谱函数。对相位谱来说：双边相位谱以单边相位谱为基础构成奇函数。
- 非周期信号的傅里叶变换
在工程技术中，周期函数可以展开成傅里叶级数，那么非周期函数呢?能否用一个周期函数逼近一个非周期函数呢?一般而言，任何一个非周期函数f(x)都可以看成是由某个周期函数fT(x)当周期T→+∞时转化而来的。为说明这一点，作周期为T的函数fT(x)使其在$[-\frac{T}{2},\frac{T}{2}]$之内等于f(x)，而在$[-\frac{T}{2},\frac{T}{2}]$之外按周期T的函数fT(x)延拓出去。
$$f_T(x)=\left\{\begin{matrix}f(x),x \in[-\frac{T}{2},\frac{T}{2}]
\\ f_T(x+T),x \notin[-\frac{T}{2},\frac{T}{2}]
\end{matrix}\right.$$
T越大，fT(x)与f(x)相等的范围也越大，这表明当T→+∞时，周期函数fT(x)便可以转化为f(x)。周期T趋于无穷大，其频谱间隔将趋于无穷小，从而信号的频谱密集成为连续频谱。同时，各频率分量的幅度也趋近于无穷小，不过这些无穷小量之间仍保持一定的比例关系。为了表明无穷小的振幅之间的差别，引入一个新的量成为“频谱密度函数”。
- 离散傅里叶变换
从时域的采样数据转变为频域的算法，称为离散傅里叶变换（DFT）。DFT将采样信号的时域和频域联系起来，DFT广泛应用于谱分析、应用力学、光学、医学图像、数据分析、仪器及远程通信等方面。
假设有N个时域采样信号，对这N个样本进行DFT变换，结果仍将为N个样本，但它却是频域表示法。时域的N个样本与频域的N个样本之间的关系如下：
假设信号采样率为$f_s$，采样间隔为$\Delta t$，有$\Delta t=1/f_s$，采样信号表示为$x_n,0\leqslant n \leqslant N-1$（即有$N$个样本），对这N个样本进行傅里叶变化，公式如下：
$$X_k=\sum_{n=0}^{N-1}x_n e^{-j2\pi k n/N}\quad\quad k=0,1,2,...,N-1$$
其结果$X_k$为$x_n$对应的频域表示。注意时域和频域中均有N个样本，同时域中的时间间隔对应的频域间隔$\Delta f$为：
$$\Delta f = \frac{f_s}{N}=\frac{1}{N\Delta t}$$
$\Delta f$也被称为频率分辨率，增加采样次数N或减小采样频率$f_s$均能减小$\Delta f$（提高分辨率）
- DFT计算举例
下例为 N个采样点经DFT后的准确频率大小。假设$X_0$表示直流成分或信号的均值，为了便于观察对波形进行DFT后的结果，假设这个直流成分的幅度值为常数+1V，下图中列出了4个采样信号。
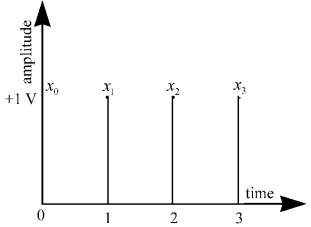
每个采样点的幅值均为+1V，按时间顺序排列：$x_0=x_1=x_2=x_3=1$，用DFT公式对这个序列进行离散傅里叶变换。
利用欧拉公式：$e^{-j\theta}=\cos{\theta}-j\sin{\theta}$就可以得到：
$X_0=\sum_{n=0}^{N-1}x_n e^{-j2\pi n\times 0/N}=x_0+x_1+x_2+x_3=4$
$X_1=x_0+x_1(\cos{\frac{\pi}{2}}-j\sin{\frac{\pi}{2}})+x_2(\cos\pi-j\sin\pi)+x_3(\cos{\frac{3\pi}{2}}-j\sin{\frac{3\pi}{2}})=1-j-1+j=0$
$X_2=x_0+x_1(\cos\pi-j\sin\pi)+x_2(\cos2\pi-j\sin2\pi)+x_3(\cos 3\pi-j\sin 3\pi)=1-1+1-1=0$
$X_3=x_0+x_1(\cos{\frac{3\pi}{2}}-j\sin{\frac{3\pi}{2}})+x_2(\cos 3\pi-j\sin 3\pi)+x_3(\cos{\frac{9\pi}{2}}-j\sin{\frac{9\pi}{2}})=1+j-1-j=0$
因此，除了直流成分$X_0$外，其它值均为0。$X_0$的值取决于采样次数$N$，由于$N=4$，所以$X_0=4$，若$N=10$，则$X_0=10$。其它的值$X_k$也同样依赖于$N$的大小；因此为了得知频率成分的大小，经常将DFT的结果除以$N$。
在Mathematica中使用Fourier函数可以很方便的计算离散傅里叶变换：
- 计算离散傅里叶变换
DFT公式为:$X_k=\sum_{n=0}^{N-1}x_n e^{-j2\pi k n/N}$，从形式上看它是一个线性运算：向量$\vec{x}$的矩阵乘法（利用矩阵M将其变换到频域空间）
$$\vec{X}=M \vec{x}$$
矩阵M(N行N列)可以表示为：
$$M_{kn}=e^{-j2\pi kn/N}$$
这么想的话，我们可以简单地利用矩阵乘法计算DFT：
import numpy as np def DFT(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] # the number of samples n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x) test_data =[1,1,1,1] print DFT(test_data)
结果如下：
我们可以对比numpy中的FFT函数：
可以看出FFT计算出了相同的结果，但是两者所花费的时间差别巨大（在ipython中进行测试）：
%timeit %run dft.py
%timeit np.fft.fft(x)
测试结果为：
100 loops, best of 3: 2.84ms per loop
100000 loops, best of 3: 5.09us per loop
可以看出这种简单的DFT计算方法，比FFT慢了几个数量级。一般来说$x_n$和$ e^{-j2\pi k n/N}$都是复数，因此每计算一个$X_k$，需要N次复数乘法和N-1次复数加法，而k取值从0到N-1，所以完成整个DFT运算总共需要N2次复数乘法和N(N-1)次复数加法。在这些运算中乘法运算要比加法运算复杂，需要的时间也多一些。因为复数运算实际上是由实数运算来完成的，这时DFT计算公式可写为：
$$X_k=\sum_{n=0}^{N-1}(a+jb)(c+jd)$$
的形式，由此可见，1次复数乘法需要4次实数乘法和2次实数加法；1次复数加法需要2次实数加法。因而每运算一个$X_k$需要4N次实数乘法和2N+2(N-1)=2(2N-1)次实数加法。所以整个DFT运算总共需要4N2次实数乘法和2N(2N-1)次实数加法。
从上面统计可以看到，直接计算DFT，乘法次数和加法次数都是与N2成正比的，当N很大时，运算量是很大的，有时甚至无法忍受。例如对一幅N×N的图像进行DFT变化，当N=1024时，直接计算DFT所需复数乘法次数为1012次，如果用每秒做一千万次复数乘法的计算机，即使不考虑加法运算时间，也需要近28个小时。对实时性要求很高的信号处理来说，只有改进DFT计算方法，减少复数乘法、加法的运算次数。
- 快速傅里叶变换（FFT）
快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。对于长度为N的输入矢量，FFT是O(N logN)级的，而普通DFT算法是O(N^2)级的。
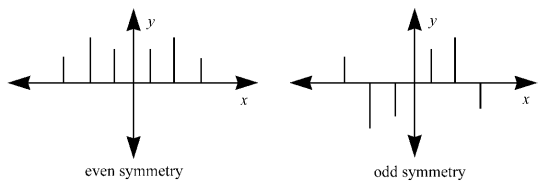
FFT是怎么快速计算的呢？答案就在于它利用了对称性。从DFT计算公式可看出，不管输入信号$x_n$是实数还是复数，$X_k$总是复数(也可能虚数部分为零),它包含两部分:幅值和相位。可以证明，对于实信号$x_n$，其DFT具有对称的性质：
$|X_k|=|X_{N-k}|$
$phase(X_k)=-phase(X_{N-k})$
即幅值偶对称，相位奇对称（下标为k和N-k的两个复数共轭）。偶对称指信号关于y轴对称，奇对称指信号关于原点对称，如下图所示：
下面的例子演示了这一个规律，先以rand随机产生有8个元素的实数数组x，然后用fft对其运算之后，观察其结果为8个复数：
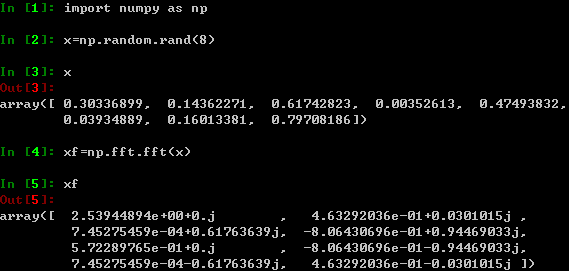
可以看出第(1、7)，(2、6)，(3、5)个复数互为共轭复数。DFT变换后的复数数组的另一规律是：下标为0和N/2的两个复数的虚数部分为0。下面让我们来看看FFT变换之后的那些复数都代表什么意思。
- 首先下标为0的实数（数组中第一个元素）表示了时域信号中的直流成分的多少
- 下标为k的复数a+b*j表示时域信号中周期为N/k个取样值的正弦波和余弦波的成分的多少，其中a表示cos波形的成分，b表示sin波形的成分
我们再来看一下$X_{N+k}$的值，根据DFT公式，可以推出
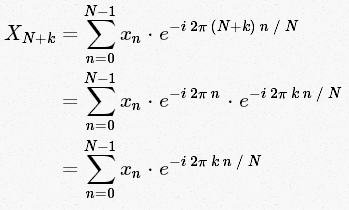
根据欧拉公式，对于所有的整数n，$e^{-i 2\pi n}=1$，则有:$X_{N+k}=X_k$或者$X_{k+i\times N}=X_k$，这体现了变换系数(矩阵)的周期性。利用对称性和周期性，DFT运算中有些项便可以合并，并能将长序列的DFT分解为短序列的DFT进行运算。而DFT的运算量是与$N^2$成正比的，所以N越小越有利。
DFT的计算可以分为两部分。设序列长度为N，并且满足N为2的整数次幂。按照n的奇偶性把$x_n$分解为两个N/2点的子序列:
$$\left\{\begin{matrix}x(2m)=x_1(m)
\\ x(2m+1)=x_2(m)\quad m=0,1,2,...,\frac{N}{2}-1
\end{matrix}\right.$$
则从DFT的定义可得：
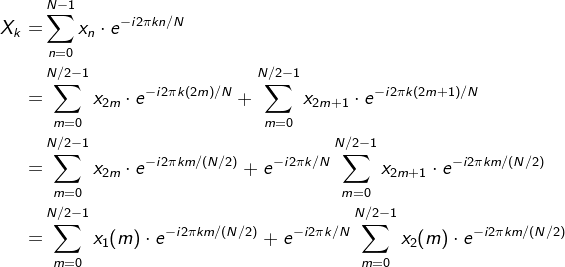
从而N个点序列的离散傅里叶变换分解为N/2个点序列的离散傅里叶变换来实现。用序列$X_1(k)$、$X_2(k)$分别表示$x_1(m)$和$x_2(m)$的N/2点DFT，即：
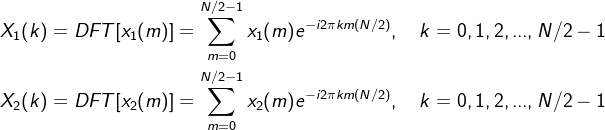
所以
$$X(k)=X_1(k)+e^{-i2\pi k/N}\cdot X_2(k), \quad k=0,1,2,...,N/2-1 \qquad\qquad(a)$$
利用$e^{-i2\pi (k+N/2)/N}=-e^{-i2\pi k/N}$ 和序列$X_1(k)$、$X_2(k)$隐含的周期性(以N/2为周期)可以得到
$$X(k+\frac{N}{2})=X_1(k)-e^{-i2\pi k/N}\cdot X_2(k), \quad k=0,1,2,...,N/2-1 \qquad\qquad(b)$$
这样将N点的序列DFT变换分解为计算两个N/2点的DFT变换$X_1(k)$、$X_2(k)$代入式(a)，可以求得$X(k)$前一半(k=0,1,2,...,N/2-1)项数的结果，再计算(b)式得到$X(k)$的后一半(k=N/2,...,N-1)项数的结果。式(a)、(b)的运算可以用信号流程图表示出来，如下图所示。因为图形的形状类似蝴蝶结，所以称之为蝶形信号流程图。图中各支路的传递系数标注在支路的一侧，没有标注系数时，该支路系数为1。
采用这种方法，将N=8点的序列x(n)的DFT运算分解过程如下图所示（记$e^{-i2\pi k/N}=W_N^k$）：
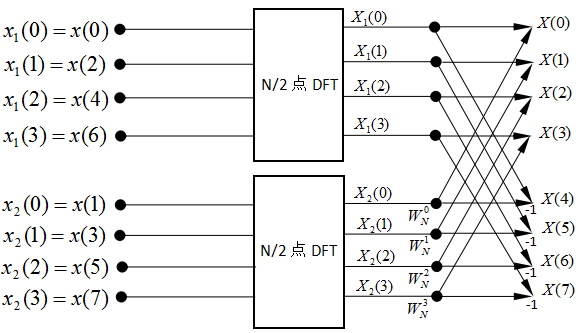
由前面的分析可以看出，每一个蝶形运算有一次复数乘法及两次复数加(减)法。而计算每个$X_1(k)$或$X_2(k)$需要N/2次复数乘法和$(\frac{N}{2}-1)$次复数加法，则每N/2点的DFT需要$(\frac{N}{2})^2=\frac{N^2}{4}$次复数乘法，和$\frac{N}{2}(\frac{N}{2}-1)$次复数加法。则N个点的DFT需要$\frac{N^2}{2}$次复数乘法和$N(\frac{N}{2}-1)$次复数加法。最后把2个N/2点的DFT合称为N点DFT时，需要进行N/2次蝶形运算，因此还需要N/2次复数乘法和N次复数加法。因此，完成N点序列的一次分解，共需要$\frac{N^2}{2}+\frac{N}{2}$次复数乘法和$\frac{N^2}{2}$次复数加法。对比前面直接计算N点DFT和进行一次分解后的计算量，可以看出进行一次分解后的运算量减少了约一半。
由于N为2的整数次幂，因而N/2仍是偶数，可以进一步把每个N/2点的子序列再按奇偶性分组为两个N/4点的子序列。
将$x_1(m)$分解为
$$\left\{\begin{matrix}x_1(2m)=x_3(m)
\\ x_1(2m+1)=x_4(m)
\end{matrix}\right.,\quad m=0,1,2,..,\frac{N}{4}-1$$
令$e^{-i2\pi k/(N/2)}=W_{N/2}^k$，则类似可以推导出：
$$\begin{align*}
\left\{\begin{matrix}X_1(k) &=X_3(k)+W_{N/2}^k \cdot X_4(k)
\\ X_1(k+\frac{N}{4}) &=X_3(k)-W_{N/2}^k \cdot X_4(k)
\end{matrix}\right.,\quad k=0,1,2,...,\frac{N}{4}-1
\end{align*}$$
$x_2(m)$也可以进行同样的分解，得到:
$$\begin{align*}
\left\{\begin{matrix}X_2(k) &=X_5(k)+W_{N/2}^k \cdot X_6(k)
\\ X_2(k+\frac{N}{4}) &=X_5(k)-W_{N/2}^k \cdot X_6(k)
\end{matrix}\right.,\quad k=0,1,2,...,\frac{N}{4}-1
\end{align*}$$
N=8时$X_3(k)$，$X_4(k)$，$X_5(k)$，$X_6(k)$都是2点的DFT，无需再分，即
$$\begin{align*}
X_3(0)=x(0)+x(4),X_3(1)=x(0)-x(4)
\\X_4(0)=x(2)+x(6),X_4(1)=x(2)-x(6)
\\X_5(0)=x(1)+x(5),X_5(1)=x(1)-x(5)
\\X_6(0)=x(3)+x(7),X_6(1)=x(3)-x(7)
\end{align*}$$
若N=16,32或2的更高次幂，可按上述方法继续分下去，直到2点的DFT为止。以上算法是按照时间下标的奇偶分开，故称为时间抽取算法（Decimation in Time,DIT）。下图是N=8序列的FFT运算的蝶形示意图。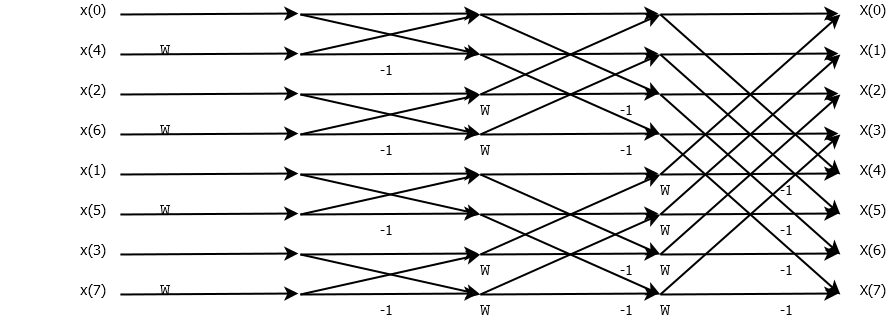
- FFT的实现
上图看出蝶形运算很有规律。N=2M点的FFT由M级运算，每级由N/2个蝶形运算组成。每一个蝶形都要乘以一个系数W，称其为旋转因子。用m表示由左向右的运算级数(m=1,2,...,M)，则图形的第m级共有2m-1个不同的因子W。当N=23=8时各级蝶形运算的旋转因子为：
m=1时，$W=W_{N/4}^p=W_{2^m}^p,\quad p=0$
m=2时，$W=W_{N/2}^p=W_{2^m}^p,\quad p=0,1$
m=3时，$W=W_N^p=W_{2^m}^p,\quad p=0,1,2,3$
对于N=2M的一般情况，第m级的旋转因子为：
$W=W_{2^m}^p,\quad p=0,1,2,...,2^{m-1}-1$，则对每一级旋转因子间的关系为：$W_{2^m}^p \cdot W_{2^m}^1=W_{2^m}^{p+1}$，其中$W_{2^m}^1=e^{-i \pi/2^{m-1}}$
每一级（每列）计算都有N/2个蝶形运算构成，第1级的N/2个蝶形结构系数都相同为$W_2^0=1$；第2级的N/2个蝶形结构有两种蝶形运算，一种系数为$W_4^0$，另一种为$W_4^1$，每种各有N/4个蝶形结构；第m级的N/2个蝶形结构共有2m-1个不同的系数。 每一个蝶形运算完成下述基本的迭代运算，在第m级有：
$$\begin{align*}
X_{m+1}(p)=X_{m}(p)+W_N^r\cdot X_{m}(q)
\\X_{m+1}(q)=X_{m}(p)-W_N^r \cdot X_{m}(q)
\end{align*}$$
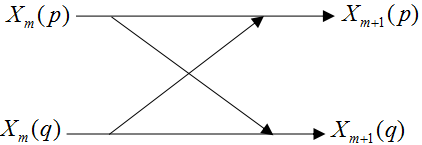
式中m表示第m列迭代，p和q表示数据所在的行数（参加蝶形运算的上、下两个节点的序号），q-p即为蝶形结的运算节点的距离，观察图中规律可知蝶形结的运算两节点间的距离为2m-1。
由8点FFT运算蝶形图可以看出，变换后的输出序列X(k)依照正序排列，但输入序列的次序不再是原来的自然顺序，这正是由于将x(n)按奇偶拆分所产生的。因此，序列在进行按时间抽取的基2-FFT算法之前，要重新排序，使之符合算法的要求，新序列是原序列的二进制码位倒置顺序，简称码位倒序。下表是N=8时序列下标之间的关系。
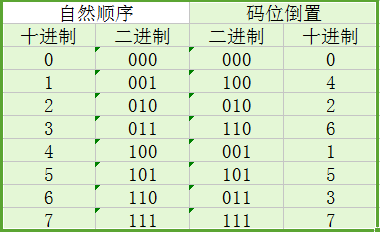
从上表可以看出自然序号加1，是在其二进制最低位加1，并逢2向高位进1。而倒序序号是在其对应的二进制最高位加1，逢2向低位进位。对于N=2M，M位二进制数各位的权值从高到低依次为N/2、N/4、...、4、2、1。因此在最高位加1，相当于十进制数加N/2。如果最高位为0，即序号小于N/4，则直接加N/2得到下一个倒序号；如果最高位为1，则最高位加1变为0后向次高位进1，相当于加N/4。实现倒序的程序代码如下：
int i, j, k; for(j = 0,i = 0; i < FFT_N-1; i++) { // 如果i<j,交换x(i)和x(j) if(i < j) { temp = xin[j]; xin[j] = xin[i]; xin[i] = temp; } // 求j的下一个倒位序 k = FFT_N / 2; // 倒序二进制最高位加1代表十进制加N/2 while(k <= j) // 如果k<=j,表示j的最高位为1,此时要向次高位进位 { j = j - k; // 加1后变成0 k = k / 2; } j = j + k; // 完成二进制最高位加1 }
代码中，i和j分别为自然序号和倒序序号，在每次循环中，当i<j时，将x(i)和x(j)交换，否则不交换。while循环语句用于实现倒序值j的计算，以便下次循环实现相应一对数据的交换。FFT算法代码如下：
#include<cmath> #include<cstdio> #define PI 3.141592653589793238462 //定义圆周率值 #define FFT_N 4 //定义傅里叶变换的点数(FFT_N应该为2的N次方) struct compx {float real,imag;}; //定义一个复数结构 compx s[FFT_N]; //定义结构体数组 // 函数功能：对两个复数进行乘法运算 compx product(struct compx a, struct compx b) { // 注意：C语言中定义结构体变量时类型名前要加关键字struct,而C++可以不加 compx c; c.real = a.real * b.real - a.imag * b.imag; c.imag = a.real * b.imag + a.imag * b.real; return c; } // 函数功能：对输入的复数组进行快速傅里叶变换（FFT） // 输入参数：*xin复数结构体组的首地址指针，struct型 void FFT(compx *xin) { /*********************** 倒序重排，完成码位倒置 ****************************/ int i, j, k; compx temp1, temp2; for(j = 0,i = 0; i < FFT_N-1; i++) { // 如果i<j,交换x(i)和x(j) if(i < j) { temp2 = xin[j]; xin[j] = xin[i]; xin[i] = temp2; } // 求j的下一个倒位序 k = FFT_N / 2; // 倒序二进制最高位加1代表十进制加N/2 while(k <= j) // 如果k<=j,表示j的最高位为1,此时要向次高位进位 { j = j - k; // 加1后变成0 k = k / 2; } j = j + k; // 完成二进制最高位加1 } /*********************** 进行各级蝶形运算 ******************************/ // 计算M的值，M为蝶形运算级数,M=log2(N) int M; int t = FFT_N; for(M = 1; (t /= 2) != 1; M++); int m; // m表示第m级蝶形 int dist; // 第m级蝶形结的运算两节点间的距离 int p, q; // p,q分别表示参加蝶形运算的上、下两个节点的序号 compx W; // 旋转因子 compx K; // 递推系数,W(p+1)=K*W(p) for(m = 1; m <= M; m++) // 控制蝶形结级数 { dist = 1<<(m-1); // dist=2^(m-1) int same = FFT_N/2/dist; // 每一级中相同系数的数目 W.real = 1.0; // 旋转因子初始值为1 W.imag = 0.0; K.real = cos(PI / dist); // 递推系数 K=e^(-i*pi/2^(m-1)) K.imag = -sin(PI / dist); for(j = 0; j <= dist-1; j++) // 控制计算不同种蝶形结，即计算系数不同的蝶形结 { for(p = j; p <= FFT_N-1; p += 2*dist ) // 控制同一蝶形结运算，即计算系数相同蝶形结 { q = p + dist; temp2 = product(W, xin[q]); // 中间变量 temp1 = xin[p]; xin[p].real = temp1.real + temp2.real; // 蝶形运算公式 xin[p].imag = temp1.imag + temp2.imag; xin[q].real = temp1.real - temp2.real; xin[q].imag = temp1.imag - temp2.imag; } W = product(K, W); // 计算第m级运算的下一旋转因子 } } } // 测试FFT变换 int main() { int i; // 给结构体赋值，采样点全部为实数 for(i = 0; i < FFT_N; i++) { s[i].real = 1.0; s[i].imag = 0.0; } FFT(s); // 进行快速傅里叶变换 for(i = 0; i < FFT_N; i++) // 输出结果 printf("%.1f+%.1fi ",s[i].real, s[i].imag); return 0; }
整个程序可以分为两部分：一部分是倒序重排，完成码位倒置。另一部分是用3个嵌套循环完成M级运算，其中最外层的一个循环控制M级的顺序运算；内层的2个循环控制同一级各蝶形结构的运算，其中最内层循环控制同一种（即$W_N^p$中的p相同）蝶形运算，而中间一层循环控制不同种（即$W_N^p$中的p不同）蝶形运算
- Python实现
我们先采用递归的方法，将采样序列分解，直到分解出来的子问题小到无法通过分治提高效率，接近极限时，这个递归是 O(n logn) 级的。这个递归算法能在python里快速实现：
# cmath provides access to mathematical functions for complex numbers from cmath import exp, pi def fft_recursive(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" N = len(x) if N <= 1: return x even = fft_recursive(x[0::2]) # start from 0, select every other element odd = fft_recursive(x[1::2]) # start from 1, select every other element T= [exp(-2j*pi*k/N)*odd[k] for k in range(N//2)] return [even[k] + T[k] for k in range(N//2)] + \ [even[k] - T[k] for k in range(N//2)] test_data = 1024*[1] fft_recursive(test_data)
在ipython中测试1024个点DFT和将其分解后再计算的FFT程序所花的时间，可以看出分而治之后程序运行速度提升了一个数量级
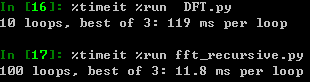
由于采用的递归调用方式，程序效率不是很高，下面我们再将其改为非递归版，取更长的序列（1024*16个采样点）进行测试
import numpy as np def fft_non_recursive(x): """non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2") # N_min here is equivalent to the stopping condition above, # and should be a power of 2 N_min = min(N, 32) # Perform an O[N^2] DFT on all length-N_min sub-problems at once n = np.arange(N_min) k = n[:, None] # k=n.reshape((N_min, 1)) M = np.exp(-2j * np.pi * n * k / N_min) X = np.dot(M, x.reshape((N_min, -1))) # build-up each level of the recursive calculation all at once while X.shape[0] < N: X_even = X[:, :X.shape[1] / 2] X_odd = X[:, X.shape[1] / 2:] factor = np.exp(-1j * np.pi * np.arange(X.shape[0])/ X.shape[0])[:, None] X = np.vstack([X_even + factor * X_odd, X_even - factor * X_odd]) return X.ravel() test_data = np.ones(1024*16) fft_non_recursive(test_data)
从下图的结果可以看出，非递归方式比递归的实现在速度上又提升了一个级别。
参考：
http://blog.jobbole.com/70549/
http://www.guokr.com/post/463448/
http://old.sebug.net/paper/books/scipydoc/fft_study.html#id1
