V-rep学习笔记：机器人逆运动学数值解法（The Pseudo Inverse Method）

　　There are two ways of using the Jacobian matrix to solve kinematics. One is to use the transpose of the Jacobian J^T. The other is to calculate the inverse of the Jacobian J^-1. J is most likely redundant and non square,thus an ordinary inverse is not possible. We can try using the pseudo inverse to find a matrix that effectively inverts a non square matrix. J⁺ is the pseudoinverse of J, also called the Moore-Penrose inverse of J . It is defined for all matrices J , even ones which are not square or not of full row rank.

　　雅可比矩阵将关节空间速度映射到直角坐标空间：ΔP = J(θ)Δθ。对于机器人运动学逆解来说可以考虑求雅克比矩阵J的逆，然后根据Δθ=J(θ)^-1ΔP计算出关节角变动量并反复迭代。然当很多情况下J不可逆，因此可以考虑求其广义逆（Moore-Penrose逆）来求解方程。设A∈C^m×n，b∈C^m，则线性方程组Ax=b有解的充分必要条件是AA⁺b=b，且通解为x=A⁺b + (I-A⁺A)y (y∈Cⁿ任意)，并且它的唯一极小范数解为x₀ = A⁺b（矩阵论简明教程 P150 A⁺在解线性方程组中的应用）。根据矩阵论（《矩阵论简明教程 第二版》 科学出版社 第6章 广义逆矩阵），设J为m×n阶实矩阵，当rankJ=m时，有J⁺ = J^T(J J^T)^-1；而当rankJ=n时，有J⁺ = (J^TJ )^-1 J^T，此时方程组J(θ)Δθ=ΔP的解唯一。 对一般机器人来说n≥m，且rankJ=m，即有J⁺ = J^T(J J^T)^-1。当n>m，即机构驱动数目多于末端自由度时，会出现多解的情况，pseudo inverse方法会寻找解向量中长度最小的一个（无穷多个解中2范数最小的解，即||Δθ₀||₂=min||Δθ||₂，称为极小范数解）

　Let  ΔP be e = t - P,where t is the target position,P is the end effector position and e is the desirable change of the end effector. The first iteration will result in a new θ from equation Δθ=J(θ)^-1ΔP. By using forward kinematics a new position P of the end effector is acquired and a new iteration begins. This is done until either e is small enough or the end effector does not move. 使用Pseudo Inverse方法求机器人逆解的基本步骤如下所示：

Operating Principle:
1. Shortest path in q-space
Advantages:
1. Computationally fast (second order method)
Disadvantages:
1. Matrix inversion necessary (numerical problems)
2. Unpredictable joint configurations
3. Non conservative

　　The pseudoinverse tends to have stability problems in the neighborhoods of singularities. At a singularity, the Jacobian matrix no longer has full row rank, corresponding to the fact that there is a direction of movement of the end effectors which is not achievable. If the configuration is exactly at a singularity, then the pseudoinverse method will not attempt to move in an impossible direction, and the pseudoinverse will be well-behaved. However, if the configuration is close to a singularity, then the pseudoinverse method will lead to very large changes in joint angles, even for small movements in the target position. In practice, roundoff errors mean that true singularities are rarely reached and instead singularity have to be detected by checking values for being near-zero. 对于平面二连杆机构，当θ₂趋近于0°或180°时，机械手接近奇异形位，关节J2速度将趋于无穷大。（参考John J.Craig. Introduction to Robotics: Mechanics and Control Chapter 5-->Section 5.8 Singularities）

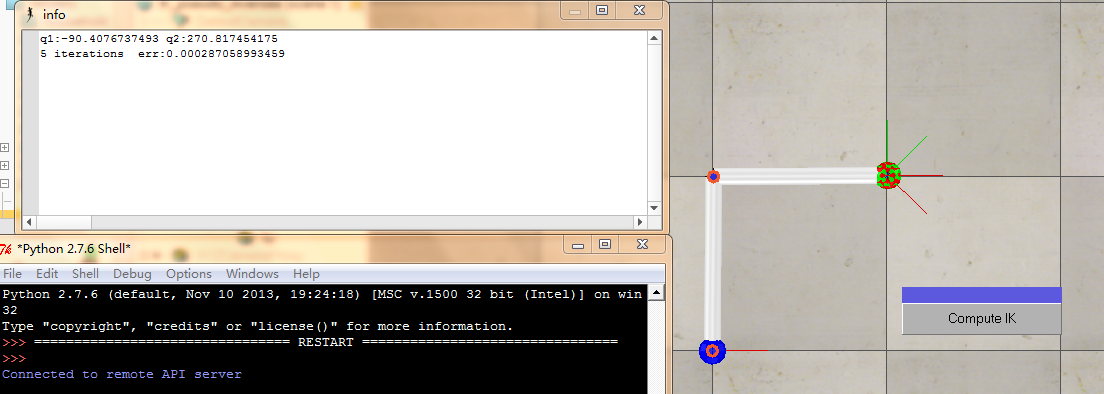
　　下面使用同样的模型验证Pseudo Inverse方法。从输出窗口可以看出，该方法迭代次数相比Jacobian Transpose法明显减少（迭代5次就达到精度要求）。The Jacobian pseudoinverse method is equivalent to solving by Newton's method.(相当于牛顿法)。Jacobian transpose is also related to solution by the method of steepest descent.（相当于最速降法或梯度法）。牛顿法是梯度法的进一步发展，梯度法在确定搜索方向时只考虑目标函数在迭代点的局部性质，即只利用一阶偏导数的信息，而牛顿法进一步利用了目标函数的二阶偏导数，考虑了梯度的变化趋势，因而可以更为全面的确定合适的搜索方向，以便很快的搜索到极小点。

import vrep             #V-rep library
import sys      
import time
import math  
import numpy as np

# Starts a communication thread with the server (i.e. V-REP). 
clientID=vrep.simxStart('127.0.0.1', 20001, True, True, 5000, 5)

# clientID: the client ID, or -1 if the connection to the server was not possible
if clientID!=-1:  #check if client connection successful
    print 'Connected to remote API server'
else:
    print 'Connection not successful'
    sys.exit('Could not connect')    # Exit from Python


# Retrieves an object handle based on its name.
errorCode,J1_handle = vrep.simxGetObjectHandle(clientID,'j1',vrep.simx_opmode_oneshot_wait)
errorCode,J2_handle = vrep.simxGetObjectHandle(clientID,'j2',vrep.simx_opmode_oneshot_wait)
errorCode,target_handle = vrep.simxGetObjectHandle(clientID,'target',vrep.simx_opmode_oneshot_wait)
errorCode,consoleHandle = vrep.simxAuxiliaryConsoleOpen(clientID,'info',5,1+4,None,None,None,None,vrep.simx_opmode_oneshot_wait)

uiHandle = -1
errorCode,uiHandle = vrep.simxGetUIHandle(clientID,"UI", vrep.simx_opmode_oneshot_wait)
buttonEventID = -1
err,buttonEventID,aux = vrep.simxGetUIEventButton(clientID,uiHandle,vrep.simx_opmode_streaming)


L1 = 0.5    # link length
L2 = 0.5
gamma = 1       # step size
stol = 1e-2     # tolerance
nm = 100        # initial error
count = 0       # iteration count
ilimit = 1000   # maximum iteration


# initial joint value
# note that workspace-boundary singularities occur when q2 approach 0 or 180 degree
q = np.array([0,1])   


while True:
    retcode, target_pos = vrep.simxGetObjectPosition(clientID, target_handle, -1, vrep.simx_opmode_streaming)


    if(nm > stol):
        vrep.simxAuxiliaryConsolePrint(clientID, consoleHandle, None, vrep.simx_opmode_oneshot_wait) # "None" to clear the console window

        x = np.array([L1*math.cos(q[0])+L2*math.cos(q[0]+q[1]), L1*math.sin(q[0])+L2*math.sin(q[0]+q[1])])
        error = np.array([target_pos[0],target_pos[1]]) - x

        J = np.array([[-L1*math.sin(q[0])-L2*math.sin(q[0]+q[1]), -L2*math.sin(q[0]+q[1])],\
                      [L1*math.cos(q[0])+L2*math.cos(q[0]+q[1]), L2*math.cos(q[0]+q[1])]])

        J_pseudo = np.dot(J.transpose(), np.linalg.inv(J.dot(J.transpose())))
        dq = J_pseudo.dot(error)
        q = q + dq

        nm = np.linalg.norm(error)

        count = count + 1
        if count > ilimit:
            vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,"Solution wouldn't converge\r\n",vrep.simx_opmode_oneshot_wait)
        vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,'q1:'+str(q[0]*180/math.pi)+' q2:'+str(q[1]*180/math.pi)+'\r\n',vrep.simx_opmode_oneshot_wait)  
        vrep.simxAuxiliaryConsolePrint(clientID,consoleHandle,str(count)+' iterations'+'  err:'+str(nm)+'\r\n',vrep.simx_opmode_oneshot_wait)   


    err, buttonEventID, aux = vrep.simxGetUIEventButton(clientID,uiHandle,vrep.simx_opmode_buffer)    
    if ((err==vrep.simx_return_ok) and (buttonEventID == 1)):
        '''A button was pressed/edited/changed. React to it here!'''
        vrep.simxSetJointPosition(clientID,J1_handle, q[0]+math.pi/2, vrep.simx_opmode_oneshot )  
        vrep.simxSetJointPosition(clientID,J2_handle, q[1], vrep.simx_opmode_oneshot )
        
        '''Enable streaming again (was automatically disabled with the positive event):'''
        err,buttonEventID,aux=vrep.simxGetUIEventButton(clientID,uiHandle,vrep.simx_opmode_streaming)

    time.sleep(0.01)

　　上面使用Python Remote API来进行逆解计算并控制V-rep中的模型（因为涉及到矩阵求逆等运算，而我不太熟悉Lua的相关数值计算库）。需要注意的是要先在V-rep模型中调用函数simExtRemoteApiStart(portNumber)开启通信服务端，然后在Python程序的客户端进行连接。