使用PCA方法创建OBB（oriented bounding-box）包围盒
碰撞检测问题在虚拟现实、计算机辅助设计与制造、游戏及机器人等领域有着广泛的应用，甚至成为关键技术。而包围盒算法是进行碰撞干涉初步检测的重要方法之一。包围盒算法是一种求解离散点集最优包围空间的方法。基本思想是用体积稍大且特性简单的几何体（称为包围盒）来近似地代替复杂的几何对象。为物体添加包围体的目的是快速的进行碰撞检测或者进行精确的碰撞检测之前进行过滤（即当包围体碰撞，才进行精确碰撞检测和处理）。包围体类型包括球体、轴对齐包围盒（AABB/Axis-aligned bounding box）、有向包围盒（OBB/Oriented bounding box）以及凸壳/凸包（Convex Hull）等。
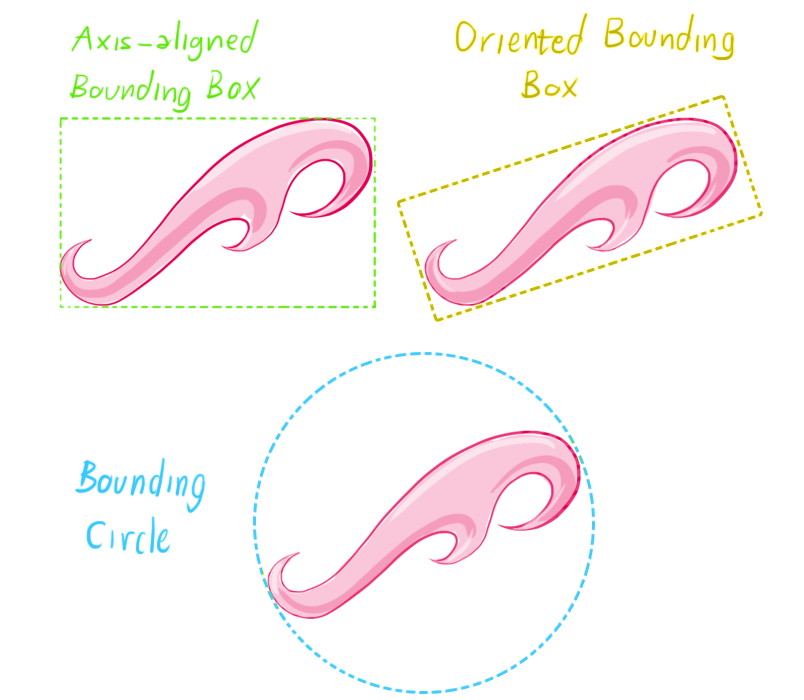
AABB是应用最早的包围盒。它被定义为包含该对象，且边平行于坐标轴的最小六面体。故描述一个AABB，仅需六个标量。AABB构造比较简单，存储空间小，但紧密性差，尤其对不规则几何形体，冗余空间很大，当对象旋转时，无法对其进行相应的旋转。包围球被定义为包含该对象的最小的球体。确定包围球，首先需分别计算组成对象的基本几何元素集合中所有元素的顶点的x，y，z坐标的均值以确定包围球的球心，再由球心与三个最大值坐标所确定的点间的距离确定半径r。包围球的碰撞检测主要是比较两球间半径和与球心距离的大小。OBB是较为常用的包围盒类型。它是包含该对象且相对于坐标轴方向任意的最小的长方体。OBB最大特点是它的方向的任意性，这使得它可以根据被包围对象的形状特点尽可能紧密的包围对象，但同时也使得它的相交测试变得复杂。OBB包围盒比AABB包围盒和包围球更加紧密地逼近物体，能比较显著地减少包围体的个数，从而避免了大量包围体之间的相交检测。但OBB之间的相交检测比AABB或包围球体之间的相交检测更费时。
OBB包围盒的生成思路简单来说就是根据一系列坐标点，通过PCA（主成分分析）获得特征向量，即OBB的主轴，推导过程可参考下面的链接。已知平面上点的坐标计算其OBB包围框四个角点以及中心的Python代码如下：
import numpy as np from scipy.spatial import ConvexHull def get_obb_from_points(points, calcconvexhull=True): """ given a set of points, calculate the oriented bounding box. Parameters: points: numpy array of point coordinates with shape (n,2) where n is the number of points calcconvexhull: boolean, calculate the convex hull of the points before calculating the bounding box. You typically want to do that unless you know you are passing in a convex point set Output: tuple of corners, centre """ if calcconvexhull: _ch = ConvexHull(points) points = _ch.points[_ch.vertices] cov_points = np.cov(points,y = None,rowvar = 0,bias = 1) v, vect = np.linalg.eig(cov_points) tvect = np.transpose(vect) # use the inverse of the eigenvectors as a rotation matrix and # rotate the points so they align with the x and y axes points_rotated = np.dot(points,np.linalg.inv(tvect)) # get the minimum and maximum x and y mina = np.min(points_rotated,axis=0) maxa = np.max(points_rotated,axis=0) diff = (maxa - mina)*0.5 # the center is just half way between the min and max xy center = mina + diff # get the corners by subtracting and adding half the bounding boxes height and width to the center corners = np.array([center+[-diff[0],-diff[1]],center+[diff[0],-diff[1]],center+[diff[0],diff[1]],center+[-diff[0],diff[1]],center+[-diff[0],-diff[1]]]) # use the the eigenvectors as a rotation matrix and # rotate the corners and the center back corners = np.dot(corners,tvect) center = np.dot(center,tvect) return corners, center
或者可以用下面的形式：
import numpy as np from scipy.spatial import ConvexHull def get_obb_from_points(points, calcconvexhull=True): """ given a set of points, calculate the oriented bounding box. Parameters: points: numpy array of point coordinates with shape (n,2) where n is the number of points calcconvexhull: boolean, calculate the convex hull of the points before calculating the bounding box. You typically want to do that unless you know you are passing in a convex point set Output: tuple of corners, centre """ if calcconvexhull: _ch = ConvexHull(points) points = _ch.points[_ch.vertices] cov_points = np.cov(points,y = None,rowvar = 0,bias = 1) v, vect = np.linalg.eig(cov_points) tvect = np.transpose(vect) # use the eigenvectors as a rotation matrix and # rotate the points so they align with the x and y axes points_rotated = np.dot(tvect, points.T) # get the minimum and maximum x and y mina = np.min(points_rotated, axis=1) maxa = np.max(points_rotated, axis=1) diff = (maxa - mina)*0.5 # the center is just half way between the min and max xy center = mina + diff # get the corners by subtracting and adding half the bounding boxes height and width to the center corners = np.array([center+[-diff[0],-diff[1]],center+[diff[0],-diff[1]],center+[diff[0],diff[1]],center+[-diff[0],diff[1]],center+[-diff[0],-diff[1]]]) # use the inverse of the eigenvectors as a rotation matrix # and rotate the corners and the center back corners = np.dot(np.linalg.inv(tvect), corners.T) center = np.dot(np.linalg.inv(tvect), center) return corners, center
代码中使用numpy.cov函数计算协方差矩阵，计算出协方差矩阵的特征向量后对原始数据进行变换，并在新的方向上计算最大最小边界。注意可以对所有原始数据进行PCA主成分分析，也可以使用scipy.spatial package提取数据的凸包（ConvexHull）上的点进行计算，参考OBB generation via Principal Component Analysis。
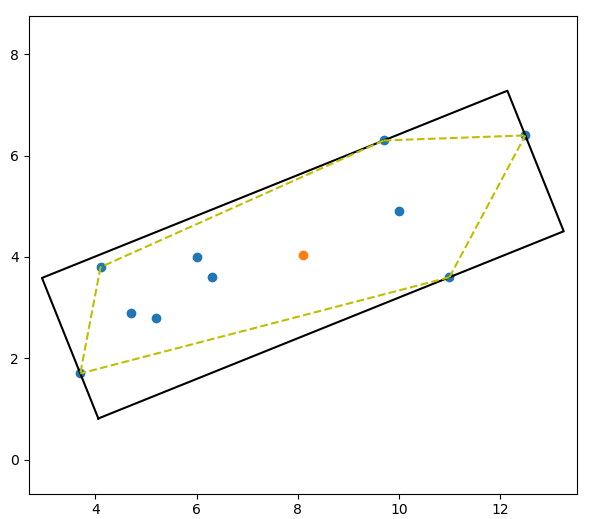
使用上面的方法计算平面上的点集np.array([(3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0,4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4)])的OBB包围盒，如下图所示，其中黄色虚线为点集的凸包：
import matplotlib.pyplot as plt import numpy as np from scipy.spatial import ConvexHull def get_obb_from_points(points, calcconvexhull=True): """ given a set of points, calculate the oriented bounding box. Parameters: points: numpy array of point coordinates with shape (n,2) where n is the number of points calcconvexhull: boolean, calculate the convex hull of the points before calculating the bounding box. You typically want to do that unless you know you are passing in a convex point set Output: tuple of corners, centre """ if calcconvexhull: _ch = ConvexHull(points) points = _ch.points[_ch.vertices] cov_points = np.cov(points,y = None,rowvar = 0,bias = 1) v, vect = np.linalg.eig(cov_points) tvect = np.transpose(vect) # use the inverse of the eigenvectors as a rotation matrix and # rotate the points so they align with the x and y axes points_rotated = np.dot(points,np.linalg.inv(tvect)) # get the minimum and maximum x and y mina = np.min(points_rotated,axis=0) maxa = np.max(points_rotated,axis=0) diff = (maxa - mina)*0.5 # the center is just half way between the min and max xy center = mina + diff # get the corners by subtracting and adding half the bounding boxes height and width to the center corners = np.array([center+[-diff[0],-diff[1]],center+[diff[0],-diff[1]],center+[diff[0],diff[1]],center+[-diff[0],diff[1]],center+[-diff[0],-diff[1]]]) # use the the eigenvectors as a rotation matrix and # rotate the corners and the center back corners = np.dot(corners,tvect) center = np.dot(center,tvect) return corners, center a = np.array([(3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0,4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4)]) fig = plt.figure(figsize=(12,12)) ax = fig.add_subplot(111) ax.scatter(a[:,0],a[:,1]) corners, center = get_obb_from_points(a) ax.scatter([center[0]],[center[1]]) ax.plot(corners[:,0],corners[:,1],'k-') hull = ConvexHull(a) for simplex in hull.simplices: plt.plot(a[simplex, 0], a[simplex, 1], 'y--') plt.axis('equal') plt.show()
参考：
OBB generation via Principal Component Analysis
如何生成OBB（OrientedboundingBox）方向包围盒
Create the Oriented Bounding-box (OBB) with Python and NumPy
