二连杆机械臂阻抗控制模拟

　　在学习机器人动力学相关内容时看到MATLAB论坛上一个有意思的仿真项目Impedance Control for a 2-Link Robot Arm - User-interactive，一个用MATLAB实现的平面二连杆机械臂阻抗控制仿真。用户可以点击并拖拽鼠标来实时改变机械臂的目标位置，在控制力矩作用下机械臂会跟随目标点运动。按空格键可以切换控制模式，此时拖拽鼠标用来给末端施加一个扰动力，由于阻抗控制的作用末端表现得像弹簧阻尼器一样，扰动力消失后末端回复到目标位置。

　　让我们来关注一下实现的细节。如下图所示，连杆1和连杆2在XY平面上通过旋转关节串联构成一个二自由度的机械臂（忽略关节摩擦等因素），重力加速度$g$沿着Y轴负方向（向量形式可写为$\mathbf{g}=[0,-g,0]^T$）。机械臂关节$a$固定在坐标原点，末端为$e$，F为作用在末端的力。$c_1$与$c_2$分别为两个连杆的质心，杆长分别为$l_1$、$l_2$，杆的质量分别为$m_1$、$m_2$，质心到关节的距离分别为$d_1$、$d_2$。$\theta_1$为与Y轴正方向的夹角($\theta_1=\theta_2=0$时机器人保持竖直状态)，$\theta_2$为连杆2与连杆1之间的夹角，是一个相对角度。

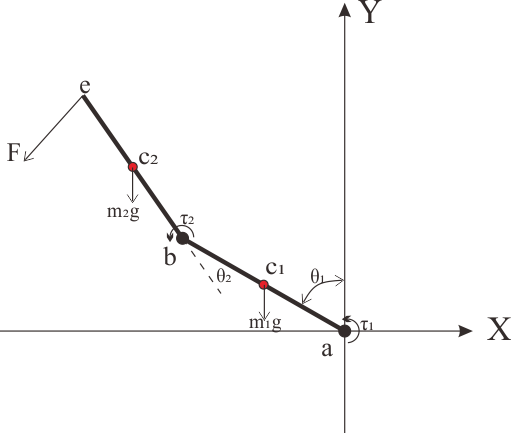
　　定义上述变量后根据理论力学等知识开始一系列计算。首先计算连杆上各点的位置坐标：

　　连杆1与连杆2在坐标系中的方向向量与角度$\theta_1$、$\theta_2$相关，其中连杆1的方向向量为$\mathbf{er_1}=\begin{bmatrix}-sin\theta_1\\ \cos\theta_1\\0\end{bmatrix}$，连杆2的方向向量为$\mathbf{er_2}=\begin{bmatrix}-sin(\theta_1+\theta_2)\\ \cos(\theta_1+\theta_2)\\0\end{bmatrix}$

　　$\mathbf{r_{ac_1}}=d_1 \cdot \mathbf{er_1}\\ \mathbf{r_{bc_2}}=d_2 \cdot\mathbf{er_2}\\ \mathbf{r_{be}}=l_2 \cdot\mathbf{er_2}\\ \mathbf{r_{ab}}=l_1 \cdot\mathbf{er_1}\\ \mathbf{r_{ac_2}}=\mathbf{r_{ab}}+\mathbf{r_{bc_2}}\\ \mathbf{r_{ae}}=\mathbf{r_{ab}}+\mathbf{r_{be}}$

 　　然后计算各点速度：连杆1上线速度的方向向量为$\mathbf{ev_1}=\begin{bmatrix}-cos\theta_1\\ -\sin\theta_1\\0\end{bmatrix}$，连杆2上线速度的方向向量为$\mathbf{ev_2}=\begin{bmatrix}-cos(\theta_1+\theta_2)\\ -\sin(\theta_1+\theta_2)\\0\end{bmatrix}$

　　$\mathbf{v_{c_1}}=d_1 \cdot \dot{\theta_1} \cdot\mathbf{ev_1}\\ \mathbf{v_b}=l_1 \cdot \dot{\theta_1}\cdot \mathbf{ev_1}\\ \mathbf{v_{c_2}}=\mathbf{v_b} + d_2 \cdot (\dot{\theta_1}+\dot{\theta_2})\cdot \mathbf{ev_2}\\ \mathbf{v_e}=\mathbf{v_b} + l_2 \cdot (\dot{\theta_1}+\dot{\theta_2})\cdot \mathbf{ev_2}$

 　　接着对速度求导计算各点加速度：

 　　$\begin{align*}&\mathbf{a_{c_1}}=\dot{\mathbf{v_{c_1}}} = d_1 \cdot \ddot{\theta_1} \cdot\mathbf{ev_1} - d_1 \cdot \dot{\theta_1}^2 \cdot \mathbf{er_1}\\&\mathbf{a_b}=\dot{\mathbf{v_b}} = l_1 \cdot \ddot{\theta_1} \cdot\mathbf{ev_1} - l_1 \cdot \dot{\theta_1}^2 \cdot \mathbf{er_1}\\&\mathbf{a_{c_2}}=\dot{\mathbf{v_{c_2}}} = d_2 \cdot (\ddot{\theta_1}+\ddot{\theta_2}) \cdot\mathbf{ev_2} - d_2 \cdot (\dot{\theta_1}+\dot{\theta_2})^2 \cdot \mathbf{er_2} + \mathbf{a_b}\end{align*}$

 　　根据受力情况可计算出关节处的力矩，对于关节$b$来说出除了电机力矩$\mathbf{\tau_2}$外，杆件2自身重量以及末端上的作用力$\mathbf{F}$都会对$b$点产生力矩，因此$b$点的合力矩为：

　　$\mathbf{M_b}=(\mathbf{r_{bc_2}}\times m_2 \mathbf{g}) + (\mathbf{r_{be}}\times  \mathbf{F}) +\mathbf{\tau_2}$

 　　根据动量矩定理，杆2对$b$点的动量矩变化率$\frac{d\mathbf{L_2}}{dt} =\mathbf{M_b}$，$\frac{d\mathbf{L_2}}{dt} =I_2(\mathbf{\ddot{\theta_1}}+\mathbf{\ddot{\theta_2}})+ \mathbf{r_{bc_2}} \times m_2 \mathbf{a_{c_2}}$（质点系对任一固定点$O$的动量矩等于质点系的动量（位于质心）对$O$点之矩与质点系相对质心的动量矩的矢量和），其中$I_2$为杆2绕其质心$c_2$的转动惯量，$I_2=\frac{1}{12}m_2{l_2}^2$。根据动量矩定理可得到角加速度$\ddot{\theta_2}$与力矩$\mathbf{M_b}$的关系式。

　　对于关节$a$，外力的合力矩为：

　　$\begin{align*}\mathbf{M_a}&=(\mathbf{r_{ac_2}}\times m_2 \mathbf{g}) +(\mathbf{r_{ac_1}}\times m_1 \mathbf{g}) + (\mathbf{r_{ae}}\times  \mathbf{F}) +\mathbf{\tau_1}\\ \frac{d\mathbf{L_1}}{dt}&=I_2(\mathbf{\ddot{\theta_1}}+\mathbf{\ddot{\theta_2}})+I_1\mathbf{\ddot{\theta_1}}+ (\mathbf{r_{ac_2}} \times m_2 \mathbf{a_{c_2}}) + (\mathbf{r_{ac_1}} \times m_1 \mathbf{a_{c_1}})\end{align*}$

 　　其中$I_1$为杆1绕其质心$c_1$的转动惯量，$I_1=\frac{1}{12}m_1{l_1}^2$。根据动量矩定理$\frac{d\mathbf{L_1}}{dt} =\mathbf{M_a}$可得到角加速度$\ddot{\theta_1}$与力矩$\mathbf{M_a}$的关系式。 　　

---

　　通常可将根据动量矩定理或牛顿-欧拉法推导出的等式写为如下形式： $$\boxed{\tau = M(\theta)\ddot{\theta}+C(\theta,\dot{\theta})+G(\theta)}$$

　　如果机械臂自由度为$n$，$M(\theta)$为$n\times n$阶正定对称矩阵，$M(\theta)\ddot{\theta}$代表惯性力项。$M(\theta)$中的主对角线元素表示各连杆本身的有效惯量，代表给定关节上的力矩与产生的角加速度之间的关系，非对角线元素表示连杆之间的耦合惯量，即是某连杆的加速运动对另一关节产生的耦合作用力矩的度量 ；$C(\theta,\dot{\theta})$为$n\times 1$阶向心力和科氏力项；$G(\theta)$为$n\times 1$阶的重力项，与机器人的形位$\theta$有关。

　　在纯位置控制下施加在机械臂末端的外力并不会影响末端的运动，因为这种情况可以认为机械臂是完全刚性的。而如果要实现主动柔顺控制，即使机械臂表现出一定的柔性就需要考虑其与环境之间的相互作用。这时关节驱动力矩可写为： $$\boxed{\tau = M(\theta)\ddot{\theta}+C(\theta,\dot{\theta})+G(\theta)+J^T(\theta)F_{tip}}$$

　　上面等式中，$F_{tip}$为机械臂末端与外界环境之间的交互力，$J$为机械臂的雅可比矩阵，用于将关节空间速度映射到操作空间：$v=J\dot{\theta}$，雅可比矩阵的转置也可将操作空间中的力映射到关节空间中：$\tau=J^TF$。对于本例，机器人雅可比矩阵可用MATLAB中的函数jacobian来计算，$J=jacobian(\mathbf{r_{ae}}, [\theta_1,\theta_2])$。$J^T(\theta)F_{tip}$代表作用于机器人关节上的外界环境力矩，等式左边的$\tau$为机器人关节驱动力矩，计算出该力矩后就可以输入给机器人驱动系统，实现期望的运动。

 　　机械臂与环境交互产生的力矩可写为$\tau_{ext}=J^T(\theta)F_{tip}=\underline{J^T(\theta)[M(\ddot{x_d}-\ddot{x})+D(\dot{x_d}-\dot{x})+K(x_d-x)]}$，$x_d$和$x$分别代表目标位置和实际位置，$\dot{x_d}$和$\dot{x}$分别代表目标速度和实际速度。矩阵$K$和$D$代表与环境交互的刚度和阻尼。机械臂末端的加速度$\ddot{x}$一般难以测量，如果直接对速度进行微分又会产生大量噪声。通常对于协作型机械臂，自身重量设计的较轻，因此可以忽略其惯性，即令$M=0$。

---

 　　下面开始对动力学系统进行迭代计算，按照仿真步长对求解出的角加速度进行积分，更新机器人的关节位置和速度，并在图形界面中动态显示。

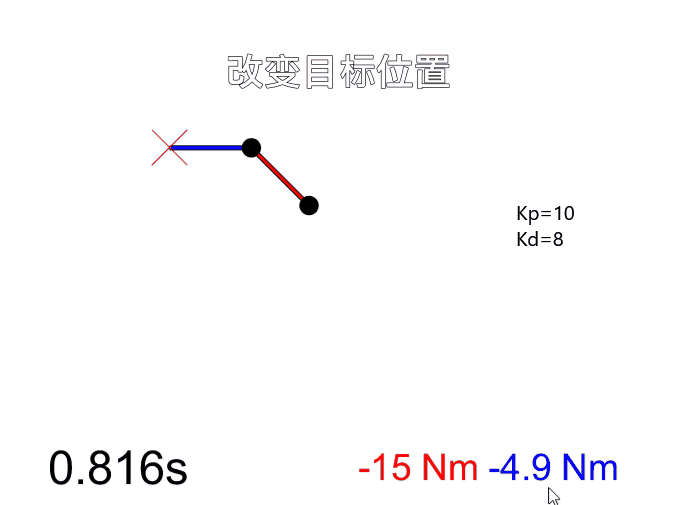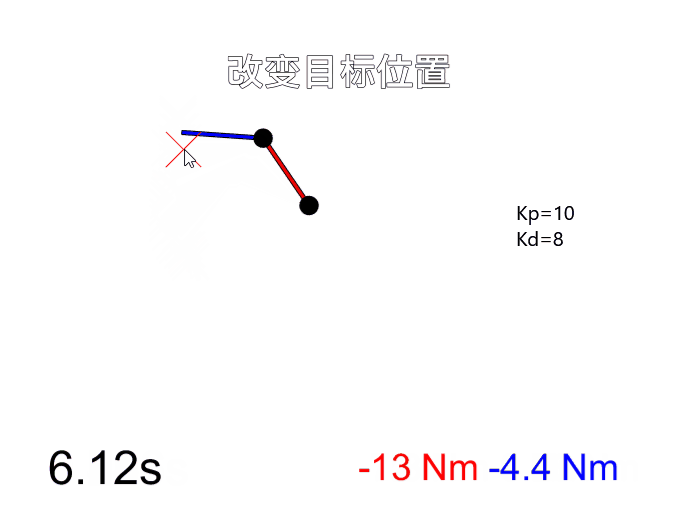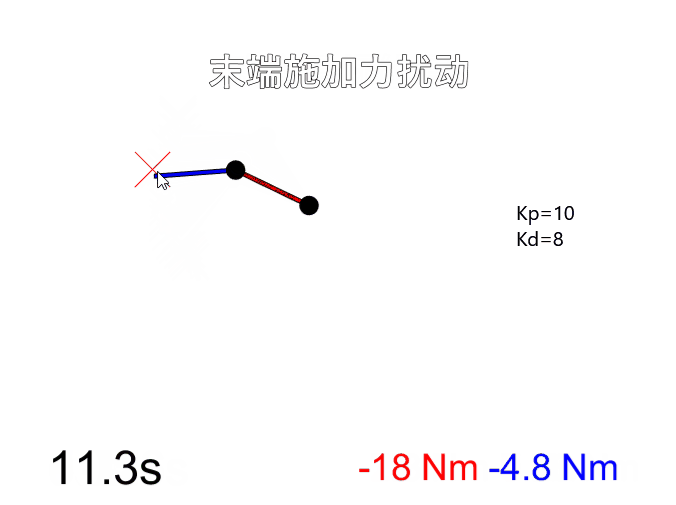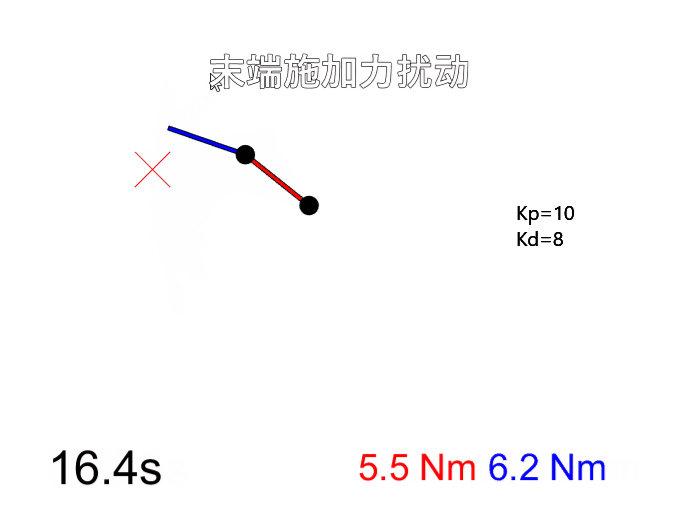
　　改变刚度和阻尼系数后（Kp=100, Kd=10），明显可以看出机器人刚性变大，在末端施加力只产生很小的形变，而且控制末端运动到目标位置时更迅速。

 

 

参考：

机器人阻抗与导纳控制

机器人单关节力矩控制

物理引擎中的刚体转动2

机器人力控制概述

Integration Basics

Impedance control—Wikipedia

Impedance Control for a 2-Link Robot Arm

Numerical Integration in Games Development

Physics for Game Programmers : Numerical Methods

Modern Robotics Mechanics, Planning, and Control