角点检测
- 理解图像特征
我们大多数人都玩过拼图游戏,首先会拿到一张完整图片的一堆碎片,要做的就是把这些碎片以正确的方式排列起来从而重建这幅图像。问题是,你怎样做到的呢?答案就是:我们要寻找一些唯一的特征,这些特征要易于被追踪和比较。以下图为例:

在图像的上方给出了六幅小图。你要做的就是找到这些小图在原始图像中的位置。A和B是平面,而且它们的图像中很多地方都存在。很难找到这些小图的准确位置。C和D简单一点,它们是建筑的边缘。你可以找到它们的近似位置,但是准确位置还是很难找到。这是因为沿着边缘,所有的地方都一样。所以边缘是比平面更好的特征,但是还不够好(在拼图游戏中要找连续的边缘)。最后E和F是建筑的一些角点,它们能很容易的被找到。因为在角点的地方,无论你向哪个方向移动小图,结果都会有很大的不同。所以可以把它们当成一个好的特征。为了更好的理解这个概念我们举个更简单的例子:

如上图所示,蓝色框中的区域是一个平面,很难被找到和跟踪:无论你向哪个方向移动蓝色框,长的都一样。对于黑色框中的区域,它是一个边缘。如果你沿垂直方向移动,它会改变;但是如果沿水平方向移动就不会改变。而红色框中的角点,无论你向哪个方向移动,得到的结果都不同,这说明它是唯一的。所以角点是一个比较好的图像特征,因为角点是两个边缘的连接点,它代表了两个边缘变化的方向上的点。图像梯度有很高的变化。这种变化是可以用来帮助检测角点的。
- Harris角点检测原理
我们已经知道了角点的一个特性:向任何方向移动变化都很大。

Chris_Harris 和 Mike_Stephens 早在 1988 年的文章《A Combined Corner and Edge Detector》中就已经提出了角点检测的方法,被称为Harris角点检测。他把这个简单的想法转换成了数学形式。将窗口向各个方向移动(u, v)然后计算所有差异的总和。
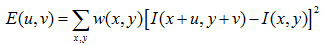
其中:

为了寻找带角点的窗口,我们搜索像素灰度变化较大的窗口。于是,我们希望找到使下式的值尽量大的点:

根据二元函数的泰勒展开公式有:

则式子可以展开为:

也可以写为下面的矩阵形式:

对于局部微小的移动量(u, v),E(u,v)可近似表达为:

其中M是2×2的对称矩阵(将窗函数考虑进去),可由图像的导数求得(Ix和Iy是图像在x和y方向的导数,可以使用函数cv2.Sobel()计算得到):
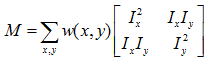
将实对称矩阵M对角化处理,λ1和λ2是矩阵M的特征值 ,这里可以把R看成旋转因子:

可以把矩阵M理解为一个二维随机分布的协方差矩阵。协方差矩阵中对角线元素表示各方向(维度)上的方差,而非对角线上的元素表示的是各个维度之间的相关性。
角点:最直观的印象就是在水平、竖直两个方向上灰度值变化均较大的点,即 λ1、λ2都较大 ;
边缘:仅在水平、或者仅在竖直方向有较大的变化量,即λ1和λ2只有一个较大 ;
平坦地区:在水平和竖直方向上的灰度值变化均较小,即λ2、λ2都很小。
解特征向量需要比较大的计算量,由于两个特征值的和等于矩阵M的迹,两个特征值的积等于矩阵M的行列式。所以用下式来判定角点质量。(k常取0.04-0.06)
$$R=det(M)-k \cdot trace(M)^2$$
其中:det(M) = λ1 λ2,trace(M) = λ1 + λ2
- 当 λ1和λ2都小时, |R|也小,这个区域就是一个平坦区域;
- 当 λ1≫ λ2 或者 λ1≪ λ2,时R小于0,这个区域是边缘;
- 当 λ1 和 λ2 都很大,并且λ1~λ2 中的时,R也很大,说明这个区域是角点。
Harris角点检测算法就是对角点响应函数R进行阈值处理:R > threshold,即提取R的局部极大值

- OpenCV中的Harris角点检测
Open中的函数cv2.cornerHarris()可以用来进行角点检测:
import cv2 import numpy as np img = cv2.imread('chessboard.jpg') gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) gray = np.float32(gray) # cv2.cornerHarris(src, blockSize, ksize, k) --> dst # 参数 img - 数据类型为float32的输入图像 # 参数 blockSize – 角点检测中要考虑的领域大小 # 参数 ksize - Sobel求导中使用的窗口大小 # 参数 k - Harris角点检测方程中的自由参数,取值范围为[0,04, 0.06] # 返回值:dst – Image to store the Harris detector responses. It has the type CV_32FC1 and the same size as src dst = cv2.cornerHarris(gray, 2, 3, 0.04) # result is dilated for marking the corners, not important dst = cv2.dilate(dst, None) # Threshold for an optimal value, it may vary depending on the image. img[dst > 0.01*dst.max()] = (0,0,255) cv2.imshow('dst', img) if cv2.waitKey(0) & 0xff == 27: cv2.destroyAllWindows()

有时我们需要最大精度的角点检测。OpenCV为我们提供了函数cv2.cornerSubPix(),它可以提供亚像素级别的角点检测。下面是一个例子。首先我们要找到 Harris角点,然后将角点的重心传给这个函数进行修正。 Harris角点用红色像素标出,绿色像素是修正后的像素。在使用这个函数是我们要定义一个迭代停止条件。当迭代次数达到或者精度条件满足后迭代就会停止。我们同样需要定义进行角点搜索的邻域大小。
下面代码使用OpenCV3.2.0,需要注意的是与OpenCV2相比有一些函数调用方式发生了改变。比如在OpenCV2.X版本中画矩形的函数没有返回值
Python: cv2.rectangle(img, pt1, pt2, color[, thickness[, lineType[, shift]]]) --> None
而在OpenCV3.2中画矩形的函数有返回值:
Python:cv2.rectangle(img, pt1, pt2, color[, thickness[, lineType[, shift]]]) --> img

import cv2 import numpy as np img = cv2.imread('test.png') gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) # find Harris corners gray = np.float32(gray) dst = cv2.cornerHarris(gray, 2, 3, 0.04) dst = cv2.dilate(dst, None) ret, dst = cv2.threshold(dst,0.01*dst.max(),255,cv2.THRESH_BINARY) dst = np.uint8(dst) # find centroids ret, labels, stats, centroids = cv2.connectedComponentsWithStats(dst) # define the criteria to stop and refine the corners: (type, maxCount, epsilon) criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 100, 0.001) # Refines the corner locations corners = cv2.cornerSubPix(gray,np.float32(centroids),(5,5),(-1,-1),criteria) # Now draw them res = np.hstack((centroids, corners)) # np.int0 可以用来省略小数点后面的数字 res = np.int0(res) img[res[:,1],res[:,0]] = [0,0,255] img[res[:,3],res[:,2]] = [0,255,0] cv2.imwrite('subpixel.png',img)
下图为寻找到的黑色填充五角星(无轮廓)的一个角点处放大图

对于棋盘格,OpenCV有专门的函数findChessboardCorners用来寻找棋盘图的内角点位置:
import numpy as np import cv2 # termination criteria criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001) img = cv2.imread("Chessboard.png") gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) # Finds the positions of internal corners of the chessboard. # The function returns a non-zero value if all of the corners are found, otherwise it returns 0 # Parameters: # image – Source chessboard view. It must be an 8-bit grayscale or color image. # patternSize – Number of inner corners per a chessboard row and column # flags – Various operation flags that can be zero or a combination of values ret, corners = cv2.findChessboardCorners(gray, (9,6), None) # The detected coordinates are approximate, and to determine their positions more accurately, the function # calls cornerSubPix(). You also may use the function cornerSubPix() with different parameters if returned # coordinates are not accurate enough. corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria) # Draw and display the corners # Python: cv2.drawChessboardCorners(image, patternSize, corners, patternWasFound) --> image # Parameters: # patternWasFound – Parameter indicating whether the complete board was found or not. # The return value of findChessboardCorners() should be passed here. img = cv2.drawChessboardCorners(img, (9,6), corners2, ret) cv2.imwrite('img.png',img)

- Shi-Tomasi角点检测
Shi-Tomasi算法是他们在1994年发表的文章《 Good Features to Track》中提出的一种Harris算法的改进。我们知道 Harris 角点检测的打分公式为:
$$R=\lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2$$
但Shi-Tomasi使用的打分函数为:
$$R = min(\lambda_1,\lambda_2)$$
即若两个特征值中较小的一个大于最小阈值,则认为它是一个角点。我们可以把它绘制到λ1 ~ λ2空间中,就会得到下图:

从这幅图中,我们可以看出来只有当λ1和λ2 都大于最小值时,才被认为是角点(绿色区域)。
OpenCV提供了函数:cv2.goodFeaturesToTrack()。这个函数可以帮我们使用Shi-Tomasi方法获取图像中N个最好的角点。通常情况下,输入的应该是灰度图像。然后确定你想要检测到的角点数目,再设置角点的质量水平。其值在0到1之间,它代表了角点的最低质量,低于这个数的所有角点都会被忽略。最后在设置两个角点之间的最短欧式距离。根据这些信息,函数就能在图像上找到角点。所有低于质量水平的角点都会被忽略,然后再把合格角点按角点质量进行降序排列。函数会采用角点质量最高的那个角点(排序后的第一个),然后将它附近(最小距离之内)的角点都删掉。按着这样的方式最后返回 N 个最佳角点。
在下面的例子中,我们试着找出图中的30个最佳角点:
import numpy as np import cv2 from matplotlib import pyplot as plt img = cv2.imread('test.png') gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) ''' Python: cv2.goodFeaturesToTrack(image, maxCorners, qualityLevel, minDistance) --> corners Parameters: maxCorners – Maximum number of corners to return. If there are more corners than are found, the strongest of them is returned. qualityLevel – Parameter characterizing the minimal accepted quality of image corners. The parameter value is multiplied by the best corner quality measure, which is the minimal eigenvalue (see cornerMinEigenVal() ) or the Harris function response (see cornerHarris() ). The corners with the quality measure less than the product are rejected. For example, if the best corner has the quality measure = 1500, and the qualityLevel=0.01 , then all the corners with the quality measure less than 15 are rejected. minDistance – Minimum possible Euclidean distance between the returned corners ''' # finds the most prominent corners in the image corners = cv2.goodFeaturesToTrack(gray, 30, 0.01, 10) corners = np.int0(corners) for i in corners: x, y = i.ravel() cv2.circle(img,(x,y), 3, 255, -1) cv2.namedWindow("image", cv2.WINDOW_NORMAL) cv2.imshow('image',img) cv2.waitKey(0) cv2.destroyAllWindow("image")

参考:




