1.本周学习总结(0--2分)
1.思维导图
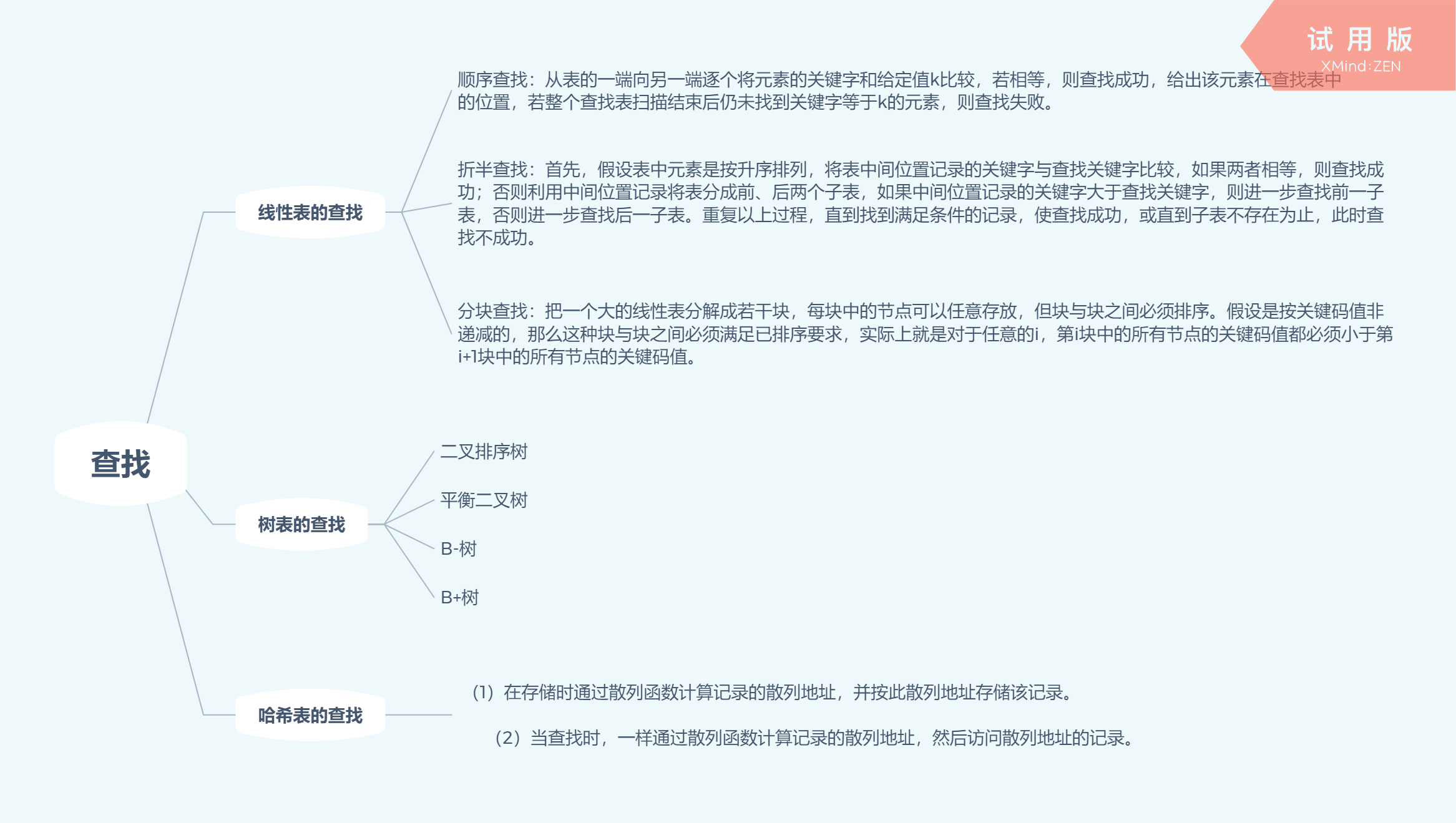
2.谈谈你对查找运算的认识及学习体会。
这两周学习的章节是查找,查找算法在上个学期和之前的章节的时候学过一些,比如顺序查找和折半查找。这些是比较简单的查找算法。本章学习了一些很难的查找算法。
本章介绍了三类查找,分别是线性表查找,树表查找和哈希表查找。线性表查找是比较简单的一类,本章学习了顺序查找,折半查找和分块查找这三种在线性表上进行查找的方法。其中折半查找的效率是这三种里面效率最高的方法。树表查找能对动态查找表进行高效率的查找。哈希表的查找需要构造哈希函数,使哈希冲突的可能性尽可能地小。
在学习查找的时候基本都是只搞懂了算法的原理而忽视了代码,所以导致课堂派的作业会写而pta上的题目不会写,所以应该要加强对代码的了解。
2.PTA实验作业(6分)
2.1.题目1:6-1 二叉搜索树的操作集 (30 分)
本题要求实现给定二叉搜索树的5种常用操作。
2.1.1设计思路(伪代码)
BinTree Insert( BinTree BST, ElementType x )
{
插入操作
}
BinTree Delete(BinTree BST,ElementType X)
{
if树空,直接输出"Not Found“
else 找到要删除的X对应结点位置
if X<当前结点 递归调用 Delete(BST->Right,X)
if X>当前结点 递归调用 Delete(BST->Left,X)
else if X=当前结点 判断当前结点左右孩子是否为空
if 左右孩子不空 调用函数FindMin(BST->Right) tmp->Data=BST->Data 保存数据 BST树的右孩子置为结点 保证二叉搜索树的有序性
else if if左孩子为空, 右孩子置为结点
if右孩子为空,右孩子置为结点
return BST
}
Position Find( BinTree BST, ElementType x )
{
if树空 return NULL
if当前结点=x return BST
else if x<当前结点 return Find(BST->Left,x)
else if x>当前结点 return Find(BST->Right,x)
return BST
}
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)


2.1.3本题PTA提交列表说明。
2.2 题目2:6-2 是否二叉搜索树 (25 分)
本题要求实现函数,判断给定二叉树是否二叉搜索树。
2.2.1设计思路(伪代码)
bool IsBST ( BinTree T )
{
if T为空 或 !T->Left&&!T->Right then 返回true
else
{
if T->Left
{
TLeft = T->Left;
while TLeft->Right then 找该点左子树最大值
}
if T->Right
{
TRight = T->Right;
hile TRight->Left then 找该点右子树最大值
}
return (T->Left?(T->Data>TLeft->Data):1)&&(T->Right?(T->Data<TRight->Data):1)
}
}
2.2.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)

2.2.3本题PTA提交列表说明。

3、阅读代码(-2--2分)
3.1 题目
写一个函数,实现一个整形有序数组的二分查找
3.2 做法解析
二分查找的思路就是折半查找,要有左边界与右边界,我们才能确定中间元素,当左边界与右边界重合的时候,这时查找对象就变为一个元素,若它不是要查找的元素,那么所查找的元素便不再数组中。这样我们就清楚地定义出所需参数,以及退出条件。
我们需要一个左边界,一个右边界,还有中间元素,若左边界大于右边界,退出循环。若找到,则返回元素所在下标。
3.3 代码截图

3.4 学习体会








