拓扑排序

拓扑排序的定义

• 具体事务进行的先后顺序
  形象地，就是依次遍历图上的结点，以保证每个点的前驱已经被访问。

AOV 网

用 DAG（有向无环图）表示一个工程，顶点表示活动，有向边 \((u,v)\) 表示活动 \(u\) 应该先于 \(v\)。

算法的抽象思想

• AOV 网中选择一个入度为 \(0\) 的顶点输出
• 从网中删除该点和所有以该点为起点的边。
• 重复前两步骤直到 AOV 网为空或当前网中不存在入度为 \(0\) 的顶点为止。
  AOV 是 DAG 的工程形式，所以有环的图是没有拓扑排序的，因为它不是 DAG，这是一个不可能有拓补排序的图：
  

图示

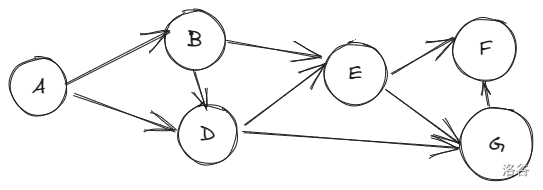
queue: a
res: 

queue: b d
res: a

queue: e g
res: a b d

queue: f
res: a b d e g

queue:
res: a b d e g f

拓扑排序的代码实现

预备工作

用 innode 数组表示每个点的入度。g 表示一个图，定义形式：vct<int> g[N]，则需要有代码来计算入度：

rep(i, 1, n) {
	for (int v : g[i]) {
		innode[v]++;
	}
}

队列实现

大家刚刚也在演示过程里见到了，笔者使用了队列形式。

所以自然地，拓扑排序可以使用队列实现：

vct<int> res;
void AovSort(int n) {
	queue<int> q;
	int k = 0;
	repq(i, 0, n) {
		if (!innode[i]) {
			q.push(i);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		res.push_back(u);
		for (int v : g[u]) {
			if (!--innode[v]) {
				q.push(v);
			}
		}
	}
}