【笔记】最短路总结

最短路 #图论

UPD: 2024/02/20 添加 Dijkstra 的路径记录，上算法课的时候临时学的。
UPD: 2024/04/27 添加 Floyd 判断负环

算法描述

对于一个图 \(G\)，找出一条从 \(s\) 到 \(t\) 的路径，使得上面的权值和最小。

Floyd

多源最短路算法，就是 dp 的一种。容易实现，支持负权边，不支持负环，适用于无向图有向图，代码如下：

rep(i, 1, n) {
    rep(j, 1, n) {
        rep(k, 1, n) {
            f[i][j][k] = min(f[i - 1][j][k], f[i - 1][j][i] + f[i - 1][i][k]);
        }
    }
}

显然 \(f\) 为 dp 数组，f[0][i][j] 表示方法如下：

• \(i=j\)，\(f_{0,i,j}=0\)。
• \(i\) 与 \(j\) 之间没有边，\(f_{0,i,j}=+\infty\)。
• 否则，为点 \(i\) 与点 \(j\) 的边的权值。

另外，\(f\) 数组的首个下标可优化：

rep(k, 1, n) {
    rep(i, 1, n) {
        rep(j, 1, n) {
            f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
        }
    }
}

时间复杂度：\(O(n^3)\)。

空间复杂度：\(O(n^2)\) 或 \(O(n^3)\)。

Floyd 判断负环

当 dp[i][i] < 0 时，有负环。

证明：\(i\) 到 \(i\) 点的最短路小于 \(0\) 时，证明存在一个到自身小于 \(0\) 的最短路，也是环。

Dijkstra

一种贪心算法，只适用于非负权边的单源最短路算法。

先定一个起点 \(s\)，并将点分为两个不同的集合：\(S\) 表示已经确认最短路的点，\(T\) 表示尚未确认最短路的电脑。设数组 \(d\)，初始化 \(d_s=0\)，其余均为 \(\infty\) 。

重复这些操作（直到 \(T\) 为空）：

• 取出 \(T\) 中最短路长度最小的点加入 \(S\)。
• 对新加点的出边执行一次松弛（即比较，对与这个出边 \((u,v,w)\)，若 \(d_v>d_u+w\)，更新 \(d_v\)。
  时间复杂度 \(O(n^2)\)。

暴力算法：

struct edge {
	int v, w;
}
vector<edge> e[N];
int d[N], vis[N]; // 注意访问过的点不能再去访问啦。

void dijkstra(int n, int s) {
	memset(d, 127, sizeof(d));
	dis[s] = 0;
	rep(i, 1, n) {
		int u = 0, INF = 1234567890;
		rep(j, 1, n) {
			if (!vis[j] && d[i] < INF) { // 没访问过且有最短路
				INF = d[i];
				u = j;
			}
			vis[u] = 1;
			for (auto E : e[u]) {
				// 这里如果 u = 0 其实默认已经干掉了
				int v = E.v, w = E.w;
				if (d[v] > d[u] + w) {
					d[v] = d[u] + w;
					// 松弛
				} 
			}
		} 
	}
}

Dijkstra 的路径记录

记数组 path[v] 为结点 \(v\) 的前驱，在松弛时做更新，那有代码：

if (d[v] > d[u] + w) {
	d[v] = d[u] + w;
	path[v] = u; // 记录前驱
}

输出方法如下：

vct<int> res;
res.push_back(end);
int x = end;
res.push_back(x);
while (path[x]) {
	res.push_back(path[x]);
	x = path[x];
}
for (int i = path.size() - 1; i >= 0; i--) {
	cout << path[i] << ' ';
}

这段作者临时补充，没经过代码验证，请大家不要直接使用。

Dijkstra 的优先队列优化

观测到暴力代码有一个不足之处：它必须通过遍历来寻找 \(T\) 集合中最短路最小的，这里我们用优先队列优化：因为优先队列可以自行排序 \(T\) 集合，这样大大降低了复杂度：降到了 \(O(m \log m)\)（因为优先队列堆排序也需要 \(\log m\) 时间）。

代码如下：

int head[N], vis[N], dis[N], n, m, s, tot;
struct edge {
    int u, v, w, next;
}e[M];
struct node {
    int w, now;
    bool operator < (const node &x) const {
        return w > x.w;
    }
};
priority_queue<node> q;

void dijkstra() {
    rep(i, 1, n) {
        dis[i] = INF;
    }
    dis[s] = 0;
    q.push({0, s});
    while (q.size()) {
        node frt = q.top(); q.pop();
        int u = frt.now;
        if (vis[u]) {
            continue;
        }
        vis[u] = 1;
        for (int i = head[u]; i; i = e[i].next) {
            int v = e[i].v;
            if (dis[v] > e[i].w + dis[u]) {
                dis[v] = e[i].w + dis[u];
                q.push({dis[v], v});
            }
        }
    }
}

Dijkstra 正确性证明

其实我自己也不会，感谢某知乎网友的文章。

使用归纳法。

设 \(S\) 为 \(\{v_{x_1},v_{x_2},v_{x_3},\ldots,v_{x_k}\}\)。

1. \(v_{x_1}\) 显然是最短路径。
2. 设第 \(k\) 次加入的 \(v_{x_k}\) 为最短路径，那么第 \(k+1\) 次加入的 \(v_{x_{k+1}}\) 仍为最短路径。
3. 反证，若 \(v_{x_{k+1}}\) 非最短路径。那必定存在另一条路径为最短的，设 \(v_u\) 为该路径中不在 \(S\) 的点，那么存在 \(d_{v_u}<d_{v_{x_{k+1}}}\) ，dijkstra 第一个步骤为从 \(T\) 基于 \(d\) 数组选取最小的一个加入 \(S\) 集合，因此 \(d_{v_{x_{k+1}}} \le d_{v_u}\) 。矛盾，得证。

Bellman-Ford

和 Dijkstra 一样，也是基于 relax 完成的最短路算法。可以求出有负权的图的最短路，还可以判断最短路是否存在。

本段摘自 OI-WIKI。

过程

松弛操作不用再讲了，就是：

\[d_u=\min\{d_v,d_u+w_{u,v}\} \]

这么做为啥这不废话吗，想想就能明白，\(u\) 与 \(v\) 连通的情况下就是将 \(d_u\) 已有的最短路与 \(d_v\) 以及 \(w_{u,v}\) 的和作比较。

与 Dijkstra 不同的是，Bellman-Ford 尝试对图上的每一条边做松弛，每过一轮循环，就对循环到的这个点的所有边尝试做一次松弛，直到松弛不了一点。

时间复杂度：考虑最坏情况，最坏情况你说能是啥？不就是每一次循环都会把所有边都给串上嘛！Bellman-Ford 最多进行 \(n-1\) 次松弛，循环是 \(m\) 次。复杂度就是 \(O(nm)\)。

Bellman-Ford 判负环

Bellman-Ford 还有一个神奇的用法：判负环。因为到了个负环这松弛操作就像永动机一样停不下来了。前面时间复杂度已经论证了松弛最多搞 \(n-1\) 轮，因此当最后所有都遍历完了还能松弛就代表有负环。

这样做其实不严谨，如果只是这样做，只能证明源点 \(s\) 无法抵达负环。最好是建一个点 \(0\)，然后把它和所有点连一条权值为 \(0\) 的边，再去跑 Bellman-Ford。像这样：

rep(i, 1, n) {
	add(0, i, 0);
	// void add(u, v, w);
}

Code

Talk is cheap. Show me your code.

struct edge {
	int u, v, w;
};
vector<edge> E;
int dis[N];
bool bellmanford(int n, int s) {
	memset(dis, 0x3f, sizeof(dis));
	// 不 memset 见祖宗
	dis[s] = 0;
	bool flg = 0;
	rep(i, 1, n) {
		flg = 0;
		for (auto [u, v, w] : edge) {
			if (dis[u] == INF) {
				continue;
			}
			// 没最短路的松弛没啥用
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w; flg = 1; // 注意说明是可以松弛的，flg = 0 代表没法松弛了
				flg = 1;
			}
		}
		if (!flg) {
			break;
		}
		// 无法松弛就 Over 了
	}
	return flg;
}

SPFA

关于 SPFA，她死了；关于 NOIP，他死了；关于 CCF，它死了。

NOIP2019

SPFA 全称 Shortest Path Faster Algorithm。其实很多时候有些松弛相当于脱裤子放屁。能想到，上一次被松弛了的点，所连到的边，才能引起下一次松弛。

用队列来维护【哪些结点可能会引起松弛操作】，只访问有必要访问的边即可。

SPFA 也可以来判负环，对于任意一个点最多访问 \(n-1\) 轮，因此我们搞一个数组 \(c\)，每路过一个点 \(u\) 就让 \(c_u\) 等于 \(c_u+1\)。如果哪次 \(c_u=n\) 了说明就有负环。直接掐掉。

SPFA 跑得确实很快，但数据经过构造可以退化成 \(O(nm)\)，也就是 Bellman-Ford。典型案例请辱骂某金钱收集组织。

Code

bool spfa() {
	memset(hdis, 63, sizeof(hdis));
	hdis[s] = 0, vis[s] = 1;
	queue<int> q;
	q.push(s);
	while (q.size()) {
		int u = q.front(); q.pop();
		vis[u] = 0;
		for (int i = head[u]; i; i = E[i].next) {
			int v = E[i].v;
			if (hdis[v] > hdis[u] + E[i].w) {
				hdis[v] = hdis[u] + E[i].w;
				if (!vis[v]) {
					vis[v] = 1;
					q.push(v);
					tot[v]++;
					if (tot[v] == n + 1) {
						return false;
					}
				}
			}
		}
	}
	return true;
}

缝合怪 Johnson

2024/01/17：™花了一天学 Johnson。最后发现数组开小了。

参考文献。原文写的更好，作者也是看原文学会哒。

因为太烦了实在不想单个单个写了，这里直接 copy 洛谷模板题：

【模板】全源最短路（Johnson）

题目描述

给定一个包含 \(n\) 个结点和 \(m\) 条带权边的有向图，求所有点对间的最短路径长度，一条路径的长度定义为这条路径上所有边的权值和。

注意：

1. 边权可能为负，且图中可能存在重边和自环；

2. 部分数据卡 \(n\) 轮 SPFA 算法。

输入格式

第 \(1\) 行：\(2\) 个整数 \(n,m\)，表示给定有向图的结点数量和有向边数量。

接下来 \(m\) 行：每行 \(3\) 个整数 \(u,v,w\)，表示有一条权值为 \(w\) 的有向边从编号为 \(u\) 的结点连向编号为 \(v\) 的结点。

输出格式

若图中存在负环，输出仅一行 \(-1\)。

若图中不存在负环：

输出 \(n\) 行：令 \(dis_{i,j}\) 为从 \(i\) 到 \(j\) 的最短路，在第 \(i\) 行输出 \(\sum\limits_{j=1}^n j\times dis_{i,j}\)，注意这个结果可能超过 int 存储范围。

如果不存在从 \(i\) 到 \(j\) 的路径，则 \(dis_{i,j}=10^9\)；如果 \(i=j\)，则 \(dis_{i,j}=0\)。

样例 #1

样例输入 #1

5 7
1 2 4
1 4 10
2 3 7
4 5 3
4 2 -2
3 4 -3
5 3 4

样例输出 #1

128
1000000072
999999978
1000000026
1000000014

样例 #2

样例输入 #2

5 5
1 2 4
3 4 9
3 4 -3
4 5 3
5 3 -2

样例输出 #2

-1

提示

【样例解释】

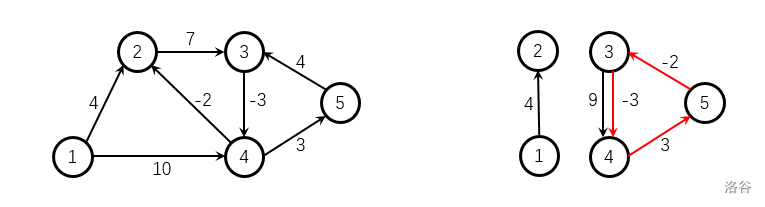
左图为样例 \(1\) 给出的有向图，最短路构成的答案矩阵为：

0 4 11 8 11 
1000000000 0 7 4 7 
1000000000 -5 0 -3 0 
1000000000 -2 5 0 3 
1000000000 -1 4 1 0 

右图为样例 \(2\) 给出的有向图，红色标注的边构成了负环，注意给出的图不一定连通。

【数据范围】

对于 \(100\%\) 的数据，\(1\leq n\leq 3\times 10^3,\ \ 1\leq m\leq 6\times 10^3,\ \ 1\leq u,v\leq n,\ \ -3\times 10^5\leq w\leq 3\times 10^5\)。

对于 \(20\%\) 的数据，\(1\leq n\leq 100\)，不存在负环（可用于验证 Floyd 正确性）

对于另外 \(20\%\) 的数据，\(w\ge 0\)（可用于验证 Dijkstra 正确性）

upd. 添加一组 Hack 数据：针对 SPFA 的 SLF 优化

解法

求多源最短路最暴力的解法当之无愧属于 Floyd，复杂度 \(O(n^3)\)。

也可以 \(n\) 次 Bellman-Ford，复杂度 \(O(n^2m)\)。SPFA 题目说了会温馨地帮您卡成 Bellman-Ford。Floyd 的 \(O(n^3)\) 受不了，Bellman-Ford 的 \(O(n^2m)\) 更难受。

队列优化完的 Dijkstra 当然更优，所以我们选择先用 SPFA 来判负环（题面说要判负环），再跑 \(n\) 次 Dijkstra。

但是，™这道题有负权……

容易想到的方法是每个边权加个 \(x\)，事完再减去 \(kx\)。但其实这是个错误的方法，考虑下图（懒得画搬 StudyingFather 的）：

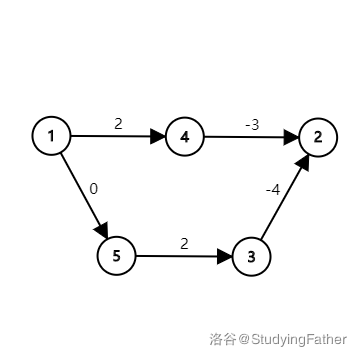
\(1\to 2\) 的最短路 \(1\to5\to3\to2\)，长度 \(-2\)。

每个边加个 \(5\)：

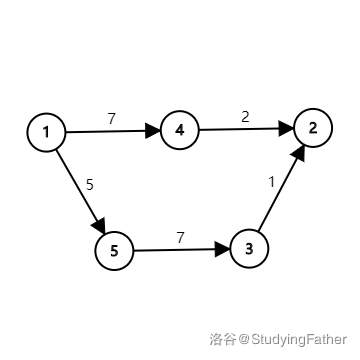
变成了 \(1\to4\to2\)。

Dijkstra，你走了我怎么活啊~~~

所以我们先建一个点 \(0\)，然后与其他所有点建边权为 \(0\) 的边。

这个工作我们要在跑 SPFA 之前完成，这里顺便再把 SPFA 跑了，注意 SPFA 这里源点要设为 \(0\)。于是我们得到了 \(0\) 点到其它所有点的最短路，记为 \(h_i\)。

这是如果 SPFA 能检查出负权边，那么直接掐掉输出即可。

接下来，对于每一条边 \((u,v,w)\) 重新将 \(w\) 赋值为 \(w+h_u-h_v\)。

接下来跑 \(n\) 轮队列优化过的 Dijkstra 即可。（厉害在队列优化）

时间复杂度：SPFA 退化后是 \(O(nm)\)，Dijkstra 是 \(O(nm\log m)\)（要跑 \(n\) 轮），合算还是 \(O(nm\log m)\)。无压力通过

证明

在重新标记后的图上，设最短路依次经过的路径为 \(p_1,p_2,\ldots,p_k\)。这条路径表达式如下：

\[(w_{p_1,p_2}+h_{p_1}-h_{p_2})+(w_{p_3,p_4}+h_{p_3}-h_{p_4})+\ldots+(w_{p_{k-1},p_k}+h_{p_{k-1}}-h_{p_k}) \]

化简后得：

\[\sum_{i=2}^k w_{p_{i-1},p_{i}}+h_{p_1}-h_{p_k} \]

前面这个求和式就是最短路。后面这俩玩意儿是不变的。

另外你可能还想要我证明 \(w_{u,v}\) 修改后为非负，也好办：一条边重新标记后的边权为 \(w'_{u,v}=w_{u,v}+h_u-h_v\)，根据松弛的公式可以发现 \(h_v\le h_u+w_{u,v}\)，因此 \(w_{u,v}\ge h_v-h_u\)，所以 \(w'_{u,v} \ge 0\)。

Code

太 ™长了，注意这道题跑完 SPFA 以及每轮 Dijkstra 数组要清空，数组要开大，因为会有新边加进来。

#include <bits/stdc++.h>
#define rty printf("Yes\n");
#define RTY printf("YES\n");
#define rtn printf("No\n");
#define RTN printf("NO\n");
#define rep(v,b,e) for(int v=b;v<=e;v++)
#define repq(v,b,e) for(int v=b;v<e;v++)
#define rrep(v,e,b) for(int v=b;v>=e;v--)
#define rrepq(v,e,b) for(int v=b;v>e;v--)
#define stg string
#define vct vector
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
#define int ll

void solve() {
	
}

const int INF = 1e9;
const int N = 1e4 + 5, M = 1e4 + 5;
int head[N], cnt, vis[N], hdis[N], tot[N], dis[N], n, m;
struct edge {
	int u, v, w, next;
}E[M];
struct node {
	int w, now;
	bool operator < (const node& x) const {
		return w > x.w;
	}
};
priority_queue<node> q;
void add(int u, int v, int w) {
	E[++cnt] = {u, v, w, head[u]};
	head[u] = cnt;
}

bool spfa() {
	int s = 0;
	memset(hdis, 63, sizeof(hdis));
	hdis[s] = 0, vis[s] = 1;
	queue<int> q;
	q.push(s);
	while (q.size()) {
		int u = q.front(); q.pop();
		vis[u] = 0;
		for (int i = head[u]; i; i = E[i].next) {
			int v = E[i].v;
			if (hdis[v] > hdis[u] + E[i].w) {
				hdis[v] = hdis[u] + E[i].w;
				if (!vis[v]) {
					vis[v] = 1;
					q.push(v);
					tot[v]++;
					if (tot[v] == n + 1) {
						return false;
					}
				}
			}
		}
	}
	return true;
}

void input() {
	cin >> n >> m;
	rep(i, 1, m) {
		int u, v, w;
		cin >> u >> v >> w;
		add(u, v, w);
	}
}

void add_edge() {
	rep(i, 1, n) {
		add(0, i, 0);
	}
	if (!spfa()) {
		cout << "-1\n";
		exit(0);
	}
	rep(u, 1, n) {
		for (int i = head[u]; i; i = E[i].next) {
			E[i].w += hdis[u] - hdis[E[i].v];
		}
	}
}

void dijkstra(int s) {
	rep(i, 1, n) {
		dis[i] = INF;
	}	
	q.push({0, s});
	memset(vis, 0, sizeof(vis));
	dis[s] = 0;
	while (q.size()) {
		node frt = q.top(); q.pop();
		int u = frt.now;
		if (vis[u]) {
			continue;
		}
		vis[u] = 1;
		for (int i = head[u]; i; i = E[i].next) {
			int v = E[i].v;
			if (dis[v] > dis[u] + E[i].w) {
				dis[v] = dis[u] + E[i].w;
				if (!vis[v]) {
					q.push({dis[v], v});
				}
			}
		}
	}
}
main() {
//	int t; cin >> t; while (t--) solve();
	input();
	add_edge();
	rep(i, 1, n) {
		dijkstra(i);
		int ans = 0;
		rep(j, 1, n) {
			if (dis[j] == INF) {
				ans += j * INF;
			} else {
				ans += j * (dis[j] + hdis[j] - hdis[i]);
			}
		}
		cout << ans << endl;
	}
	return 0;
}