【题解】医院设置
题目描述
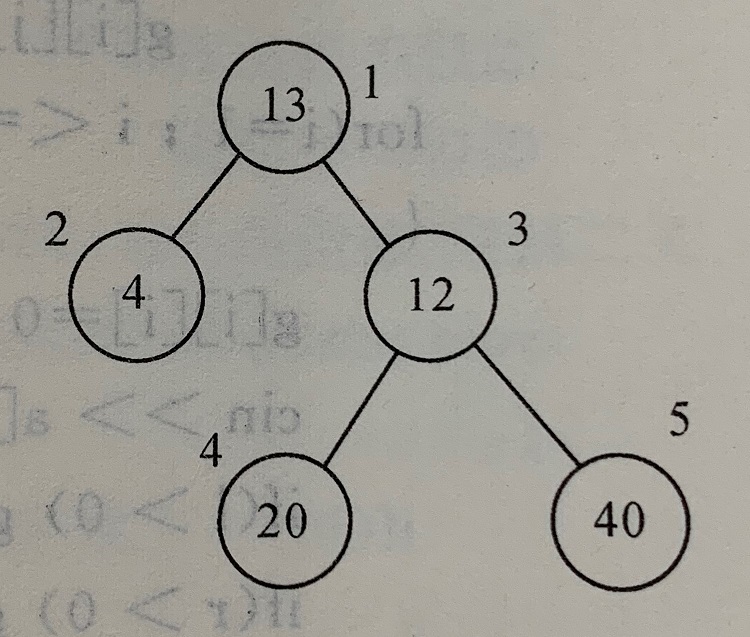
设有一棵二叉树,其中圈中的数字表示结点中居民的人口,圈边上数字表示结点编号。现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻结点之间的距离为1。就本图而言,若医院建在1处,则距离和=4+12+2×20+2×40=136;若医院建在3处,则距离和=4×2+13+20+40=81...
输入输出格式
输入格式:
第一行,一个整数n,表示树的结点数(n≤100)。
接下来的n行,每行描述了一个结点的状况,包含三个整数,整数之间用空格(一个或多个)分隔,其中:第一个数为居民人口数;第二个数为左链接,为0表示无链接;第三个数为右链接,为0表示无链接。
输出格式:
一个整数,表示最小距离和。
输入输出样例
输入样例:
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
输出样例:
81
这道题就是很简单的深搜嘛
用一个结构体储存树的一个结点的根与孩子,枚举医院的位置,深搜求路程总和即可
附代码:
#include<iostream>
using namespace std;
struct tree
{
int id,population;
int root;
int left,right;
}t[105],t2[105];
int n,mins=2147483647,target,minsum=2147483647;
void dfs(tree x,int step)
{
t[x.left].root=0;
t[x.right].root=0;
if(x.id==target)
{
mins=min(mins,step);
return;
}
if(x.left!=0) dfs(t[x.left],step+1);
if(x.right!=0) dfs(t[x.right],step+1);
if(x.root!=0) dfs(t[x.root],step+1);
}
int main()
{
cin>>n;
for(register int i=1;i<=n;++i)
{
int a,b,c;
cin>>a>>b>>c;
t[i].population=a;
t[i].id=i;t[b].id=b;t[c].id=c;
t[i].left=b;
t[i].right=c;
t[b].root=t[c].root=i;
}
for(register int i=1;i<=n;++i) t2[i]=t[i];
for(register int i=1;i<=n;++i)
{
int sum=0;
target=i;
for(register int j=1;j<=n;++j)
{
for(register int p=1;p<=n;++p) t[p]=t2[p];
mins=2147483647;
dfs(t[j],0);
sum+=mins*t[j].population;
}
minsum=min(minsum,sum);
}
cout<<minsum;
}


