leetcode 给出一个无重叠的 ，按照区间起始端点排序的区间列表。

给出一个无重叠的 ，按照区间起始端点排序的区间列表。

在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

示例 1:

输入: intervals = [[1,3],[6,9]], newInterval = [2,5]
输出: [[1,5],[6,9]]

示例 2:

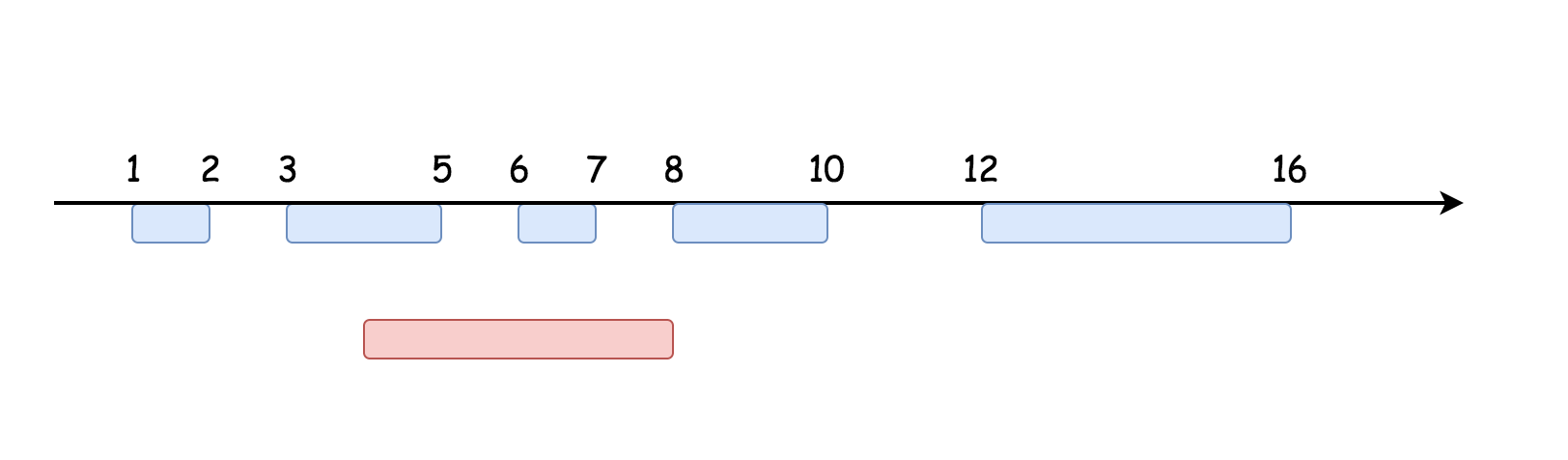
输入: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出: [[1,2],[3,10],[12,16]]
解释: 这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。

方法：贪心

贪心算法：
贪心算法一般用来解决需要 “找到要做某事的最小数量” 或 “找到在某些情况下适合的最大物品数量” 的问题，且提供的是无序的输入。

贪心算法的思想是每一步都选择最佳解决方案，最终获得全局最佳的解决方案。

标准解决方案具有 $\mathcal{O}(N \log N)$ 的时间复杂度且由以下两部分组成：

• 思考如何排序输入数据（$\mathcal{O}(N \log N)$ 的时间复杂度）。
• 思考如何解析排序后的数据（$\mathcal{O}(N)$ 的时间复杂度）

如果输入数据本身有序，则我们不需要进行排序，那么该贪心算法具有 $\mathcal{O}(N)$ 的时间复杂度。

如何证明你的贪心思想具有全局最优的效果：可以使用反证法来证明。

让我们来看下面的例子来理解：

我们可以分为三个步骤去实现它：

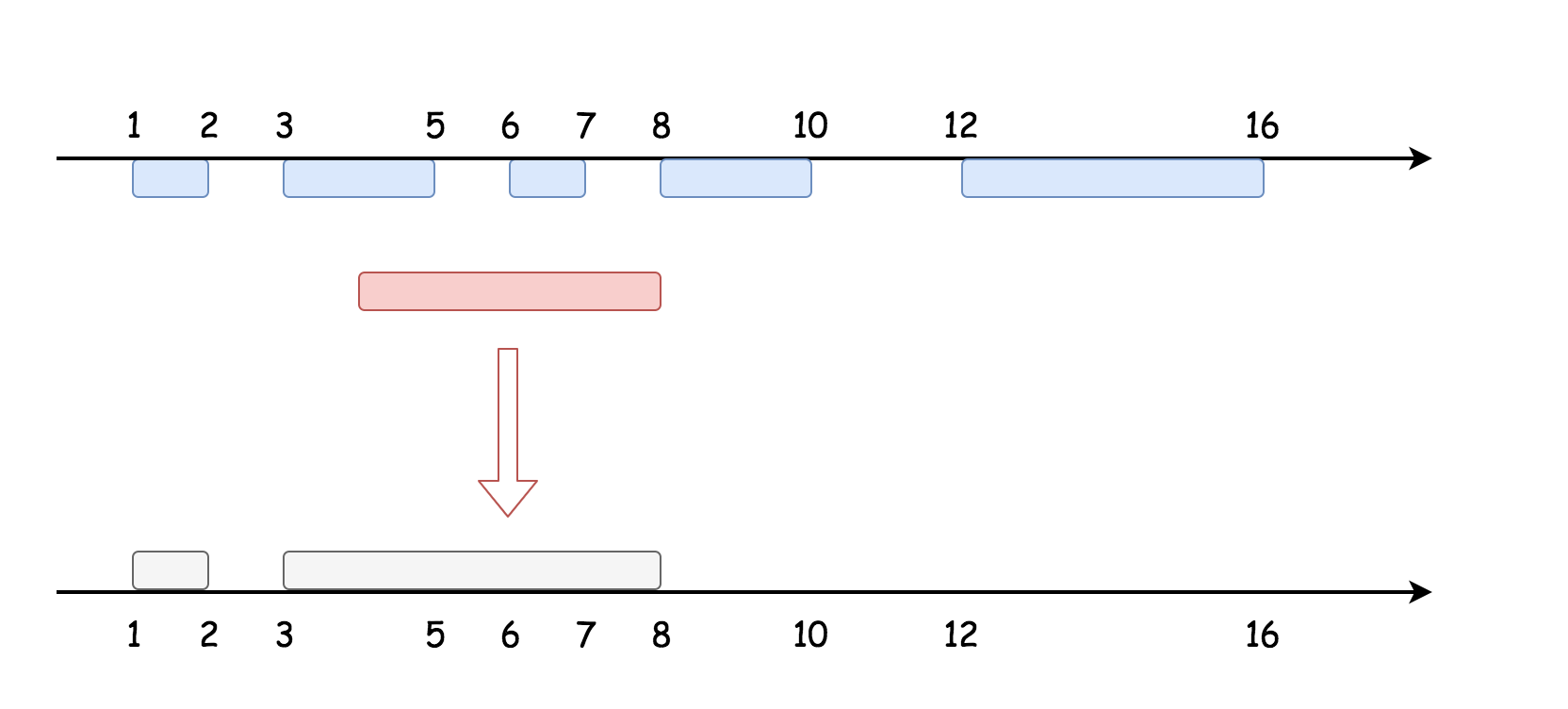
• 在区间 newInterval 之前开始的区间全部添加到输出中。

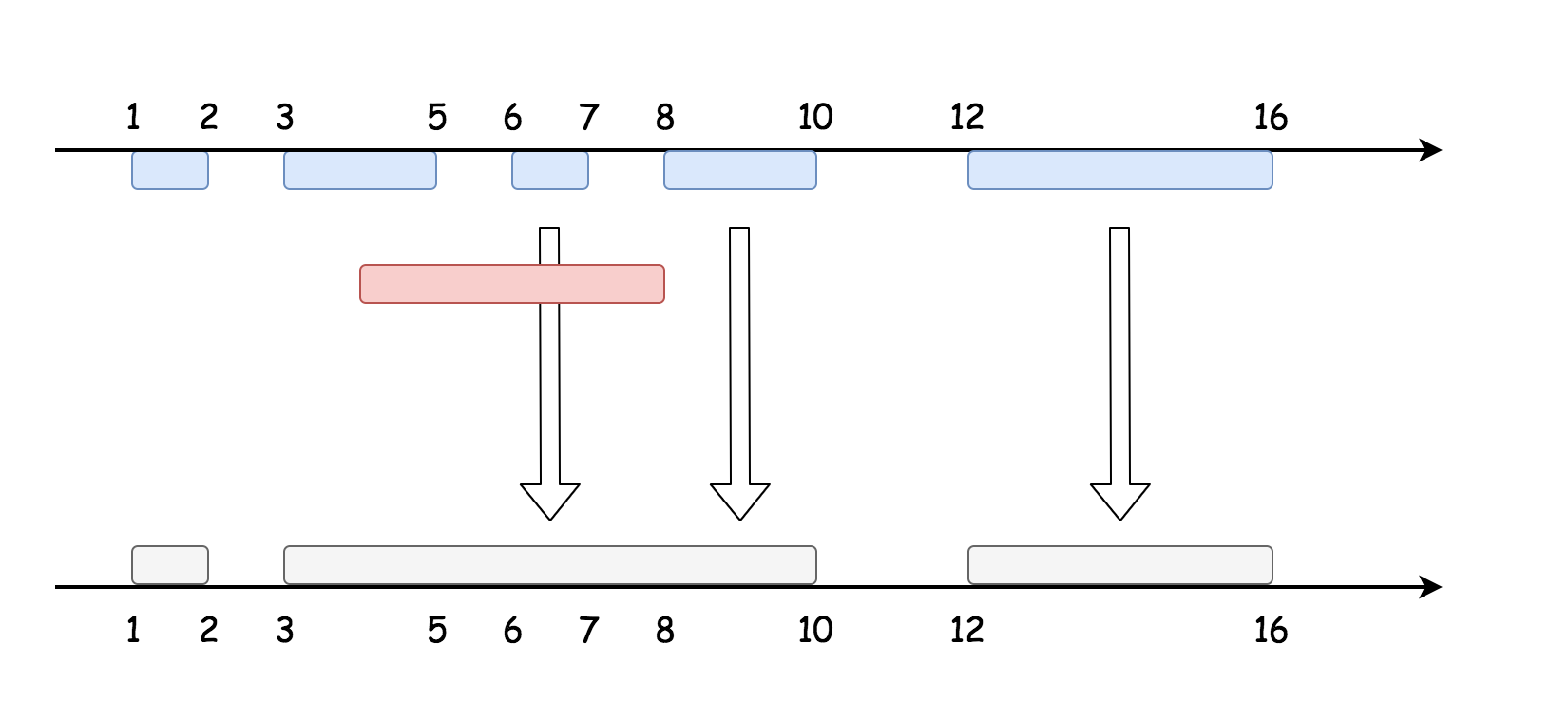
• 将 newInterval 添加到输出中，如果与输出中的最后一个区间重合则合并它们。

• 然后一个个添加后续的区间，如果重合则合并它们。

算法：

• 将 newInterval 之前开始的区间添加到输出。
• 添加 newInterval 到输出，若 newInterval 与输出中的最后一个区间重合则合并他们。
• 一个个添加区间到输出，若有重叠部分则合并他们。

• Python
• Java

class Solution:
    def insert(self, intervals: 'List[Interval]', newInterval: 'Interval') -> 'List[Interval]':
        # init data
        new_start, new_end = newInterval
        idx, n = 0, len(intervals)
        output = []
    <span class="hljs-comment"># add all intervals starting before newInterval</span>
    <span class="hljs-keyword">while</span> idx &lt; n <span class="hljs-keyword">and</span> new_start &gt; intervals[idx][<span class="hljs-number">0</span>]:
        output.append(intervals[idx])
        idx += <span class="hljs-number">1</span>
        
    <span class="hljs-comment"># add newInterval</span>
    <span class="hljs-comment"># if there is no overlap, just add the interval</span>
    <span class="hljs-keyword">if</span> <span class="hljs-keyword">not</span> output <span class="hljs-keyword">or</span> output[<span class="hljs-number">-1</span>][<span class="hljs-number">1</span>] &lt; new_start:
        output.append(newInterval)
    <span class="hljs-comment"># if there is an overlap, merge with the last interval</span>
    <span class="hljs-keyword">else</span>:
        output[<span class="hljs-number">-1</span>][<span class="hljs-number">1</span>] = max(output[<span class="hljs-number">-1</span>][<span class="hljs-number">1</span>], new_end)
    
    <span class="hljs-comment"># add next intervals, merge with newInterval if needed</span>
    <span class="hljs-keyword">while</span> idx &lt; n:
        interval = intervals[idx]
        start, end = interval
        idx += <span class="hljs-number">1</span>
        <span class="hljs-comment"># if there is no overlap, just add an interval</span>
        <span class="hljs-keyword">if</span> output[<span class="hljs-number">-1</span>][<span class="hljs-number">1</span>] &lt; start:
            output.append(interval)
        <span class="hljs-comment"># if there is an overlap, merge with the last interval</span>
        <span class="hljs-keyword">else</span>:
            output[<span class="hljs-number">-1</span>][<span class="hljs-number">1</span>] = max(output[<span class="hljs-number">-1</span>][<span class="hljs-number">1</span>], end)
    <span class="hljs-keyword">return</span> output

class Solution {

public int[][] insert(int[][] intervals, int[] newInterval) {

// init data

int newStart = newInterval[0], newEnd = newInterval[1];

int idx = 0, n = intervals.length;

LinkedList<int[]> output = new LinkedList<int[]>();

<span class="hljs-comment">// add all intervals starting before newInterval</span>
<span class="hljs-keyword">while</span> (idx &lt; n &amp;&amp; newStart &gt; intervals[idx][<span class="hljs-number">0</span>])
  output.add(intervals[idx++]);

<span class="hljs-comment">// add newInterval</span>
<span class="hljs-keyword">int</span>[] interval = <span class="hljs-keyword">new</span> <span class="hljs-keyword">int</span>[<span class="hljs-number">2</span>];
<span class="hljs-comment">// if there is no overlap, just add the interval</span>
<span class="hljs-keyword">if</span> (output.isEmpty() || output.getLast()[<span class="hljs-number">1</span>] &lt; newStart)
  output.add(newInterval);
<span class="hljs-comment">// if there is an overlap, merge with the last interval</span>
<span class="hljs-keyword">else</span> {
  interval = output.removeLast();
  interval[<span class="hljs-number">1</span>] = Math.max(interval[<span class="hljs-number">1</span>], newEnd);
  output.add(interval);
}

<span class="hljs-comment">// add next intervals, merge with newInterval if needed</span>
<span class="hljs-keyword">while</span> (idx &lt; n) {
  interval = intervals[idx++];
  <span class="hljs-keyword">int</span> start = interval[<span class="hljs-number">0</span>], end = interval[<span class="hljs-number">1</span>];
  <span class="hljs-comment">// if there is no overlap, just add an interval</span>
  <span class="hljs-keyword">if</span> (output.getLast()[<span class="hljs-number">1</span>] &lt; start) output.add(interval);
  <span class="hljs-comment">// if there is an overlap, merge with the last interval</span>
  <span class="hljs-keyword">else</span> {
    interval = output.removeLast();
    interval[<span class="hljs-number">1</span>] = Math.max(interval[<span class="hljs-number">1</span>], end);
    output.add(interval);
  }
}
<span class="hljs-keyword">return</span> output.toArray(<span class="hljs-keyword">new</span> <span class="hljs-keyword">int</span>[output.size()][<span class="hljs-number">2</span>]);

}

}

复杂度分析

• 时间复杂度：$\mathcal{O}(N)$。我们只遍历了一次输入元素。
• 空间复杂度：$\mathcal{O}(N)$，输出答案所使用的空间。