矩阵树定理学习笔记 & 洛谷 P4111 [HEOI2015]小 Z 的房间 题解

矩阵树定理

拉普拉斯矩阵

无边权

设无向图 $G$ 有 $n$ 个结点，则拉普拉斯矩阵 $L$ 是一个 $n\times n$ 的矩阵，满足：

• $L_{i,i}(i\in G)$ 的值为结点 $i$ 的度数。
• $L_{i,j}(i,j\in G,i \neq j)$ 的值为结点 $i,j$ 之间相连的边数的相反数。

如下图：

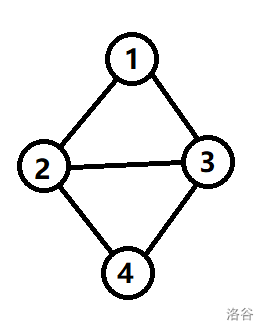
它的拉普拉斯矩阵

$$L= \begin{bmatrix} 2 & -1 & -1 &0 \\ -1 & 3 & -1 &-1 \\ -1 & -1 & 3 & -1\\ 0 & -1 & -1 &2 \end{bmatrix}$$

有边权

推广一下：

• $L_{i,i}(i\in G)$ 的值为所有与结点 $i$ 相连的边权和。
• $L_{i,j}(i,j\in G,i \neq j)$ 的值为边 $i\to j$ 的权的相反数。

定理内容

严谨的定理内容参见 OI Wiki 上对矩阵树定理的叙述。

通俗来说，把拉普拉斯矩阵去掉任意的一行一列，得到的矩阵的行列式就是原图的生成树数量（带权就是所有生成树中边的积的和）。

证明

关于这个我也不会，可以去看文末《矩阵树定理（Matrix-tree Theorem）笔记》。

求矩阵的行列式

行列式有如下性质：

• 将矩阵的两行交换，其行列式变成相反数。
• 将矩阵的一行加上（另一行乘一个数），其行列式不变。
• 三角矩阵的行列式为对角线的乘积。

利用这三条性质可以把矩阵变成三角矩阵，从而求出行列式。

比如刚才的矩阵（去掉第一行和最后一列）：

$$\begin{bmatrix} 2 & -1 & -1\\ -1 & 3 & -1\\ -1 & -1 &3 \end{bmatrix}$$

将第一行乘 $\dfrac{1}{2}$，加到第二、第三行去，再将第二行乘 $\dfrac{3}{5}$，加到第三行去，最终形成的三角矩阵：

$$\begin{bmatrix} 2 & -1 & -1\\ 0 & \dfrac{5}{2} & -\dfrac{3 }{2}\\ 0 & 0 &\dfrac{8}{5} \end{bmatrix}$$

则其行列式为 $2\times\dfrac{5}{2}\times\dfrac{8}{5}=8$。

而原图恰好有 8 个生成树：

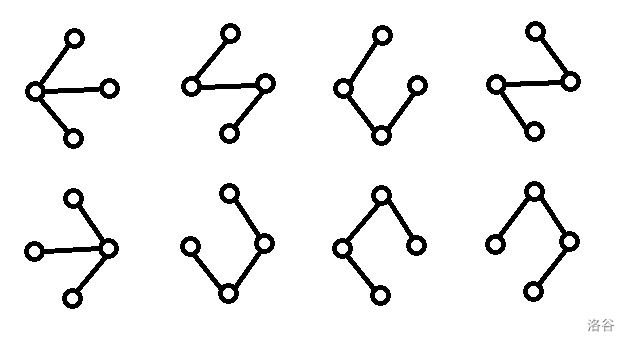
代码

回到本题，不难发现是道裸的矩阵树定理，时间复杂度 $O(n^3m^3)$。

/*
 * Title: P4111 [HEOI2015]小 Z 的房间
 * Source: 洛谷
 * URL: https://www.luogu.com.cn/problem/P4111
 * Author: Steven_lzx
 * Command: -std=c++23 -Wall -fno-ms-extensions
 * Date: 2022.11.4
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MOD=1e9;
int n,m,cnt,ans=1,laplace[100][100]/*拉普拉斯矩阵*/,id[20][20],l;
char ch[20][20];
void change(int x,int y)
{
    laplace[x][x]++;
    laplace[y][y]++;
    laplace[x][y]--;
    laplace[y][x]--;
    return;
}
signed main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            do 
                scanf("%c",&ch[i][j]);
            while(ch[i][j]!='.'&&ch[i][j]!='*');
            if(ch[i][j]=='.')
                id[i][j]=++cnt;//编号
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(ch[i][j]=='.'&&ch[i+1][j]=='.')
                change(id[i][j],id[i+1][j]);
            if(ch[i][j]=='.'&&ch[i][j+1]=='.')
                change(id[i][j],id[i][j+1]);
        }
    }
    cnt--;
    for(int i=1;i<cnt;i++)
    {
        for(int j=i+1;j<=cnt;j++)
        {
            while(laplace[j][i])
            {
                l=laplace[i][i]/laplace[j][i];
                for(int k=1;k<=cnt;k++)
                    laplace[i][k]=(laplace[i][k]-laplace[j][k]*l%MOD+MOD)%MOD;
                for(int k=1;k<=cnt;k++)
                    swap(laplace[i][k],laplace[j][k]);
                ans*=-1;
            }
        }
    }
    for(int i=1;i<=cnt;i++)
        ans=(ans*laplace[i][i]%MOD+MOD)%MOD;
    printf("%lld\n",ans);
    return 0;
}

参考资料

• 洛谷@zhy137036 在 P4111 [HEOI2015]小 Z 的房间 的题解（已不可见）。
• 知乎《矩阵树定理（Matrix-tree Theorem）笔记》。
• OI Wiki 矩阵树定理。