最大流(flow)
最大流
简要题意:
自来水厂（源点）要把水送到
n
n
n户人家，他们之间的关系构成了一个图，图上还有一个污水处理厂（汇点）
保证每户人家都有一条从源点到汇点的路径经过
图上每条水管都有一定的容量
请问自来水厂怎样才能使输水效率最高？
先了解几个定义：
流网络
流网络
G
=
(
V
,
E
)
G=(V, E)
G=(V,E)是一个有向图，其中每条边
(
u
,
v
)
(u,v)
(u,v)均有一非负容量
c
(
u
,
v
)
≥
0
c(u, v)≥0
c(u,v)≥0。
流网络中有两个特殊的顶点: 源点
s
s
s和汇点
t
t
t。
假定每个顶点都处于从源点到汇点的某条路径上，就是说，对每个顶点
v
v
v，存在一条路径
s
→
v
→
t
s \to v\to t
s→v→t
G为连通图，且
∣
E
∣
≥
∣
V
∣
−
1
|E| ≥|V|-1
∣E∣≥∣V∣−1
边的流是一个实值函数f，满足下列三个性质：
1、容量限制：对所有
u
,
v
∈
V
u,v\in V
u,v∈V ,要求
f
(
u
,
v
)
≤
c
(
u
,
v
)
f(u,v) ≤ c(u,v)
f(u,v)≤c(u,v)
理解：流量不会超过边的容量
2、反对称性：对所有
u
,
v
∈
V
u,v \in V
u,v∈V， 要求
f
(
u
,
v
)
=
−
f
(
v
,
u
)
f(u,v) = -f(v, u)
f(u,v)=−f(v,u)
理解：一个方向的流是其反方向流的相反数
3、流守恒性：对所有
u
∈
V
s
,
t
u \in V_{s, t}
u∈Vs,t，要求
∑
v
f
(
u
,
v
)
−
∑
w
f
w
,
u
=
0
\sum_vf(u,v) - \sum_wf_{w , u} = 0
∑vf(u,v)−∑wfw,u=0
理解：进入点u的总流量=离开点u的总流量
残留网络
边的残留容量：
r
(
u
,
v
)
=
c
(
u
,
v
)
−
f
(
u
,
v
)
r(u , v) = c(u , v) - f(u , v)
r(u,v)=c(u,v)−f(u,v)
残留网络：给定一流网络
G
=
(
V
,
E
)
G=(V,E)
G=(V,E)和流
f
f
f，由
f
f
f导出的
G
G
G的残留网络是
G
f
=
(
v
,
E
f
)
G_f = (v , E_f)
Gf=(v,Ef)
其中
E
f
=
(
u
,
v
)
∈
V
∗
V
:
r
(
u
,
v
)
>
0
E_f = {(u , v) \in V*V:r(u , v) > 0}
Ef=(u,v)∈V∗V:r(u,v)>0
这就是说，在残留网络中，每条边（称为残留边）能够容纳一个严格为正的网络流
当
0
<
f
(
u
,
v
)
<
c
(
u
,
v
)
0<f(u,v)<c(u,v)
0<f(u,v)<c(u,v)，如果
r
(
u
,
v
)
=
c
(
u
,
v
)
−
f
(
u
,
v
)
r(u , v) = c(u , v) - f(u , v)
r(u,v)=c(u,v)−f(u,v)
此时边(u,v)在残留网络中。
朴素做法（Ford-Fulkerson算法）：
做法
每次从源点开始找到一条路径（边的容量不为0）到汇点，更新这条路径的剩余
r
(
u
,
v
)
r(u , v)
r(u,v)
1、将
C
(
u
,
v
)
−
a
u
g
C(u , v) - aug
C(u,v)−aug
2、
C
(
v
,
u
)
+
a
u
g
C(v , u) + aug
C(v,u)+aug 给程序一次反悔的机会
如果找不到就结束。
局限分析
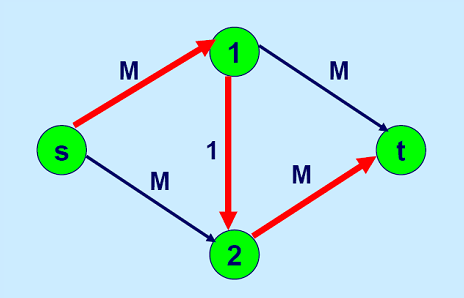
如图所示的流网络，M非常大，例如10^10。在寻找增广路时不幸按红色所示线路，那么就会不断便利边 1 → 2 1\to 2 1→2，导致时间加大很多，所以我们要想办法优化这种情况，我们加一个距离标号就好了
距离标号
数组
d
i
d_i
di存
i
i
i点到汇点的距离，
v
d
i
vd_i
vdi表示
d
中为
i
的个数
d中为i的个数
d中为i的个数
每次
d
f
s
dfs
dfs便利时只能走
d
x
=
d
t
o
+
1
d_x = d_to + 1
dx=dto+1的点，如果没有找到点符合条件，那么
d
x
=
min
与
x
相连的点
d_x = \min与x相连的点
dx=min与x相连的点
如果
v
d
vd
vd中的某个数为
0
0
0则退出
code
#include<bits/stdc++.h>
using namespace std;
const int N=205;
int n , vd[N] , d[N] , s , t , m , u , v;
long long mp[N][N] , wi;
long long dfs(int x , long long past) {
if(x == t)
return past;
long long del = 0 , now = past;
int mind = n - 1;
for(int i = 1 ; i <= n ; i++) {
if(!mp[x][i])
continue;
if(d[x] == d[i] + 1) {
del = min(mp[x][i] , now);
del = dfs(i , del);
now -= del;
mp[x][i] -= del;
mp[i][x] += del;
if(d[s] >= n)
return past - now;
if(now == 0)
break;
}
mind = min(mind , d[i]);
}
if(now == past) {
vd[d[x]] --;
if(!vd[d[x]])
d[s] = n;
d[x] = mind + 1;
vd[d[x]] ++;
}
return past - now;
}
void flow() {
long long ans = 0;
vd[0] = n;
while(d[s] < n) {
ans += dfs(s , 100000000000000000);
}
printf("%lld" , ans);
}
int main() {
scanf("%d%d%d%d" , &n , &m , &s , &t);
for(int i = 1 ; i <= m ; i++) {
scanf("%d%d%d" , &u , &v , &wi);
mp[u][v] += wi;
}
flow();
return 0;
}
