PTA前三次作业总结
PTA前三次作业总结
1.前言
第一次作业较为简单，涉及到的主要类有Scanner和String，主要题目方向为字符串判断与字符串处理，基本上一个方法即可解决题目要求，总体难度偏低。从第二次作业开始，题目开始涉及较为复杂的字符串匹配与转换，需要对String类的方法比如String.substring有一定了解，再配合一些Java自带的数据结构如ArrayList即可快速解决问题。第三次作业难度最高，需要熟练掌握Double等包装类的静态方法例如Double.parseDouble()方法，除此之外，还需要掌握正则表达式，用以完成字符串匹配，规避可能出现的格式错误。这三次作业的难度可以说是逐次递增，并且逐渐从面向过程转向面向对象，比如在第三次作业中出现了大量的代码复用，此时就需要运用方法重载来避免大量的cv操作。
2.程序设计分析
第一次作业
总体分析
类图如下：
分析：
因为第一次作业都是对不同题目语境下的简单字符串处理，因此不同类之间也不存在依赖，因此显示出的类图的模块间较为独立。
第二次作业
7-2 串口字符解析
题目：
RS232是串口常用的通信协议，在异步通信模式下，串口可以一次发送5 ~ 8位数据，收发双方之间没有数据发送时线路维持高电平，相当于接收方持续收到数据“1”（称为空闲位），发送方有数据发送时，会在有效数据（5 ~ 8位，具体位数由通信双方提前设置）前加上1位起始位“0”，在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序，模拟串口接收处理程序，注：假定有效数据是8位，奇偶校验位采用奇校验。
输入格式：
由0、1组成的二进制数据流。例如 11110111010111111001001101111111011111111101111
输出格式：
过滤掉空闲、起始、结束以及奇偶校验位之后的数据，数据之前加上序号和英文冒号。
如有多个数据，每个数据单独一行显示。
若数据不足11位或者输入数据全1没有起始位，则输出"null data"，
若某个数据的结束符不为1，则输出“validate error”。
若某个数据奇偶校验错误，则输出“parity check error”。
若数据结束符和奇偶校验均不合格，输出“validate error”。
如：11011或11111111111111111。
例如：
1:11101011
2:01001101
3:validate error
代码展示:
package Second;
import java.util.Scanner;
public class Main2 {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
String s = sc.nextLine();
if(s.length()<11)
{
System.out.print("null data");
return;
}
else if(!s.contains("0"))
{
System.out.print("null data");
}
else {
int i1=0;
int flag=1;
for(int i=0;i<s.length()-10;i++)
{
int count=0;
String str="";
if(s.charAt(i)=='0'&&i!=s.length()-1)
{
while(i1<8)
{
if(s.charAt(i+1+i1)=='1')
{
count++;
}
str+=s.charAt(i+1+i1);
i1++;
}
boolean b = (count % 2 == 0 && s.charAt(i + 9) == '0') || (count % 2 != 0 && s.charAt(i + 9) == '1');
if(s.charAt(i+10)!='1'&& (b)){
System.out.println(flag+":"+"validate error");
flag++;
}
else if(b)
{
System.out.println(flag+":"+"parity check error");
flag++;
}
else if(s.charAt(i+10)!='1')
{
System.out.println(flag+":"+"validate error");
flag++;
}
else {
System.out.println(flag+":"+str);
flag++;
}
i+=10;
i1=0;
}
}
}
}
}
类图如下：
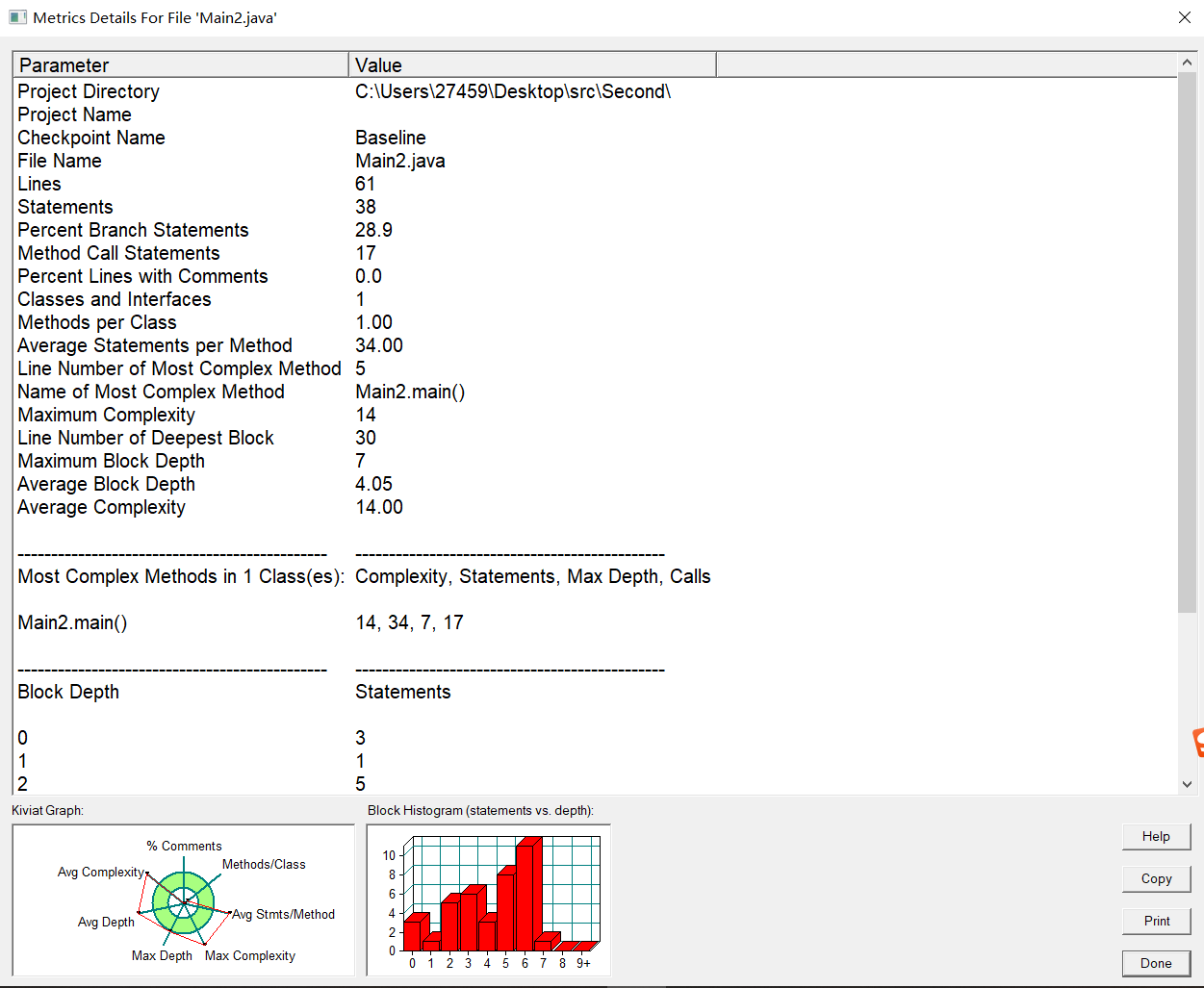
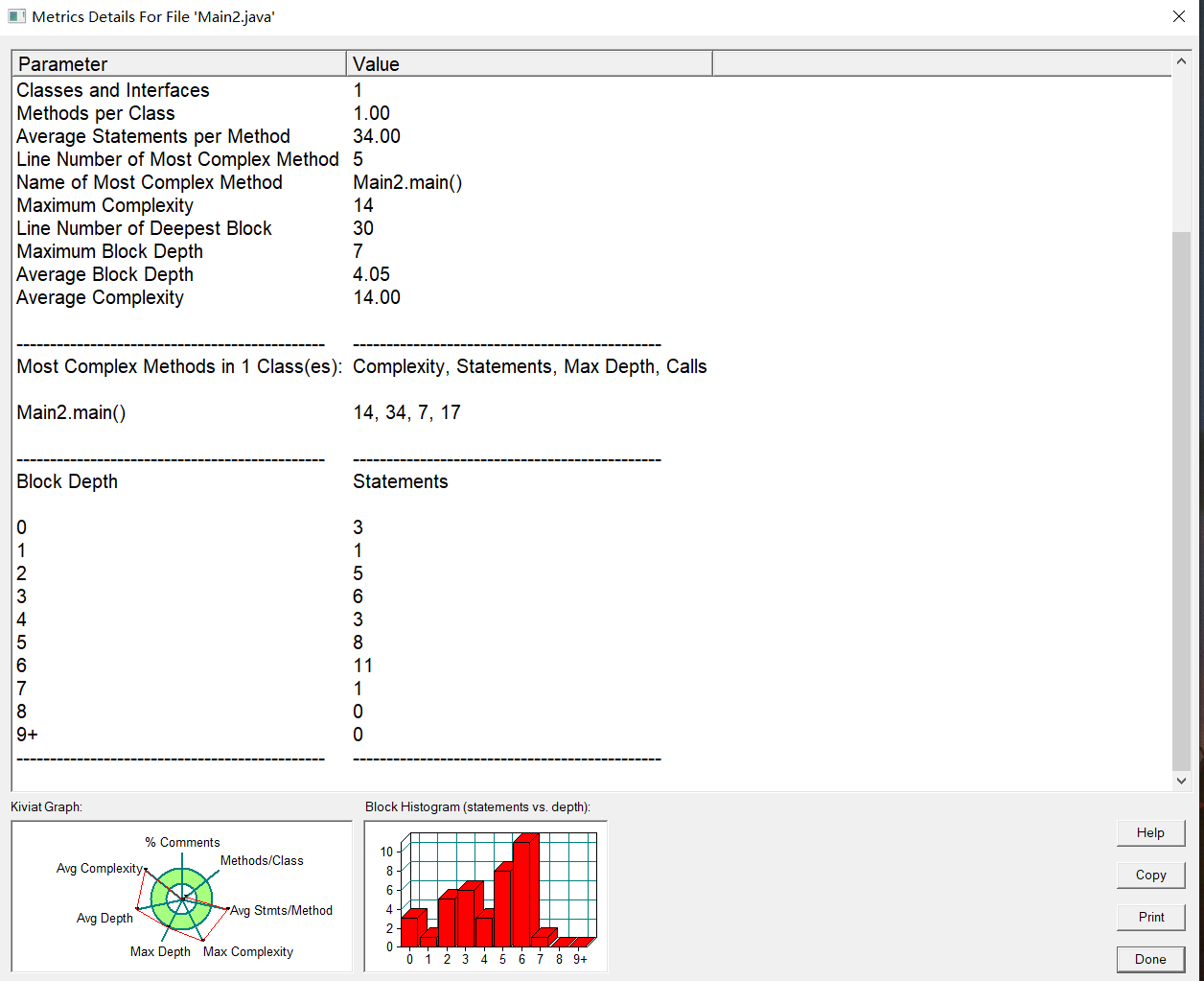
SourceMonitor的代码分析图如下：
分析如下：
1.通过运用charAt方法来获取字符串指定位置的字符，可有效避免遍历字符串带来的时间消耗，而且相对于String.substring()方法更加简便。
2.由于代码中写了较多的if~~else判断，导致该代码的环复杂度和平均深度都比较高。
3.由于只使用了一个类来实现题目要求，类图中没有其他依赖，导致代码复用性比较低。
第三次作业
7-1 点线形系列1-计算两点之间的距离
题目：
输入连个点的坐标，计算两点之间的距离
输入格式：
4个double类型的实数，两个点的x，y坐标，依次是x1、y1、x2、y2，两个点的坐标之间以空格分隔，每个点的x,y坐标以英文“,”分隔。例如：0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法，输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个，输出“wrong number of points”。
输出样例：
计算所得的两点之间的距离。例如：1.4142135623730951
代码展示：
package Third;
import java.util.Scanner;
public class Main1 {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
String s = sc.nextLine();
String[] s1 = s.split(" ");
if(s1.length>2)
{
System.out.println("wrong number of points");
return;
}
else {
String[] splits =null;
for (String s2 : s1) {
splits = s2.split(",");
for (String s3 : splits) {
if(!s3.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$"))
{
System.out.println("Wrong Format");
return;
}
}
}
splits=s.split(" ");
String[] num = splits[0].split(",");
double a = Double.valueOf(num[0]);
double b = Double.valueOf(num[1]);
num = splits[1].split(",");
double c = Double.valueOf(num[0]);
double d = Double.valueOf(num[1]);
if(a==c&&b==d){
System.out.print("Wrong Format");
return;
}
System.out.print(Math.sqrt(Math.pow((a-c),2)+Math.pow((b-d),2)));
}
}
}
类图如下：
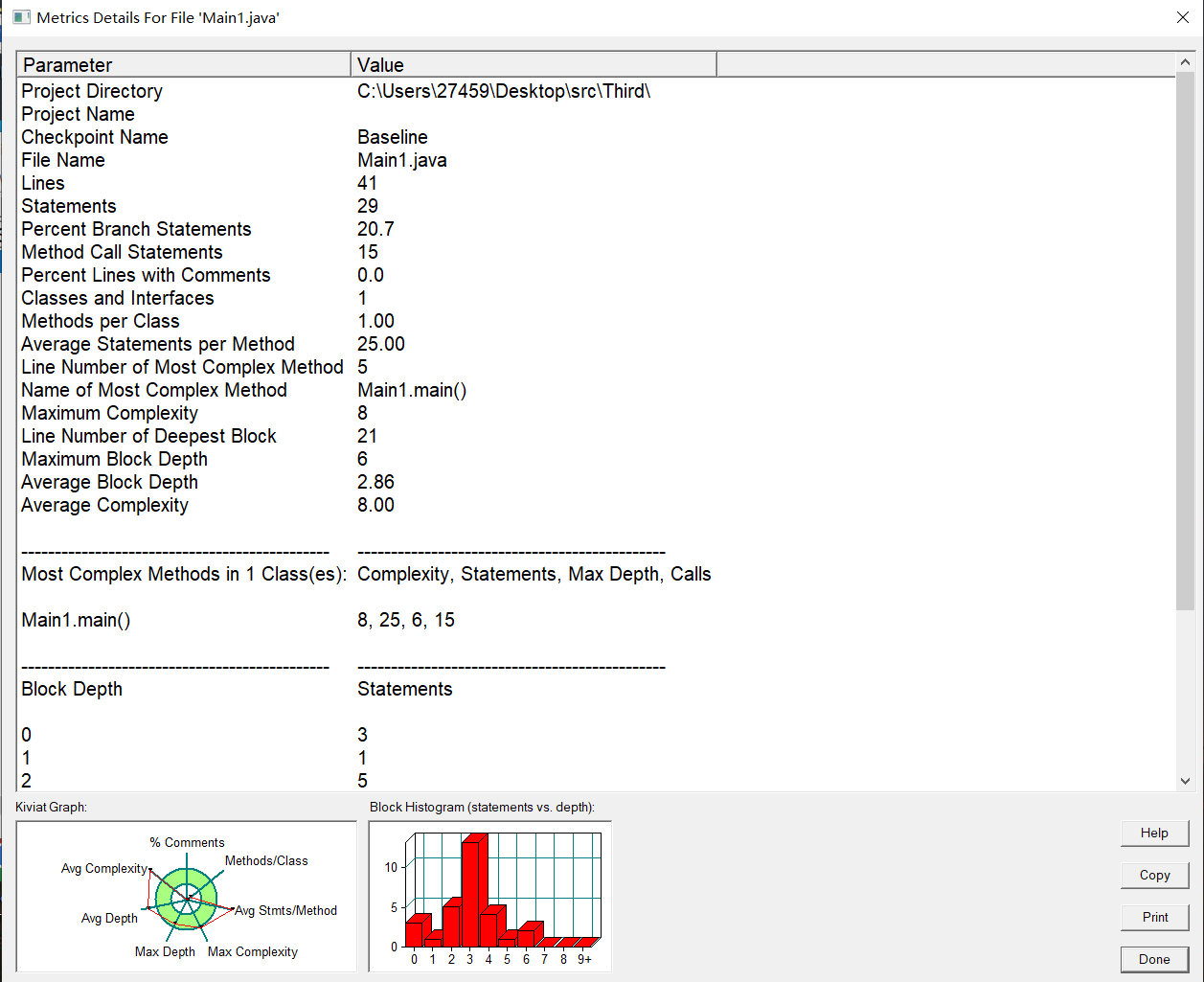
SourceMonitor的代码分析图如下：
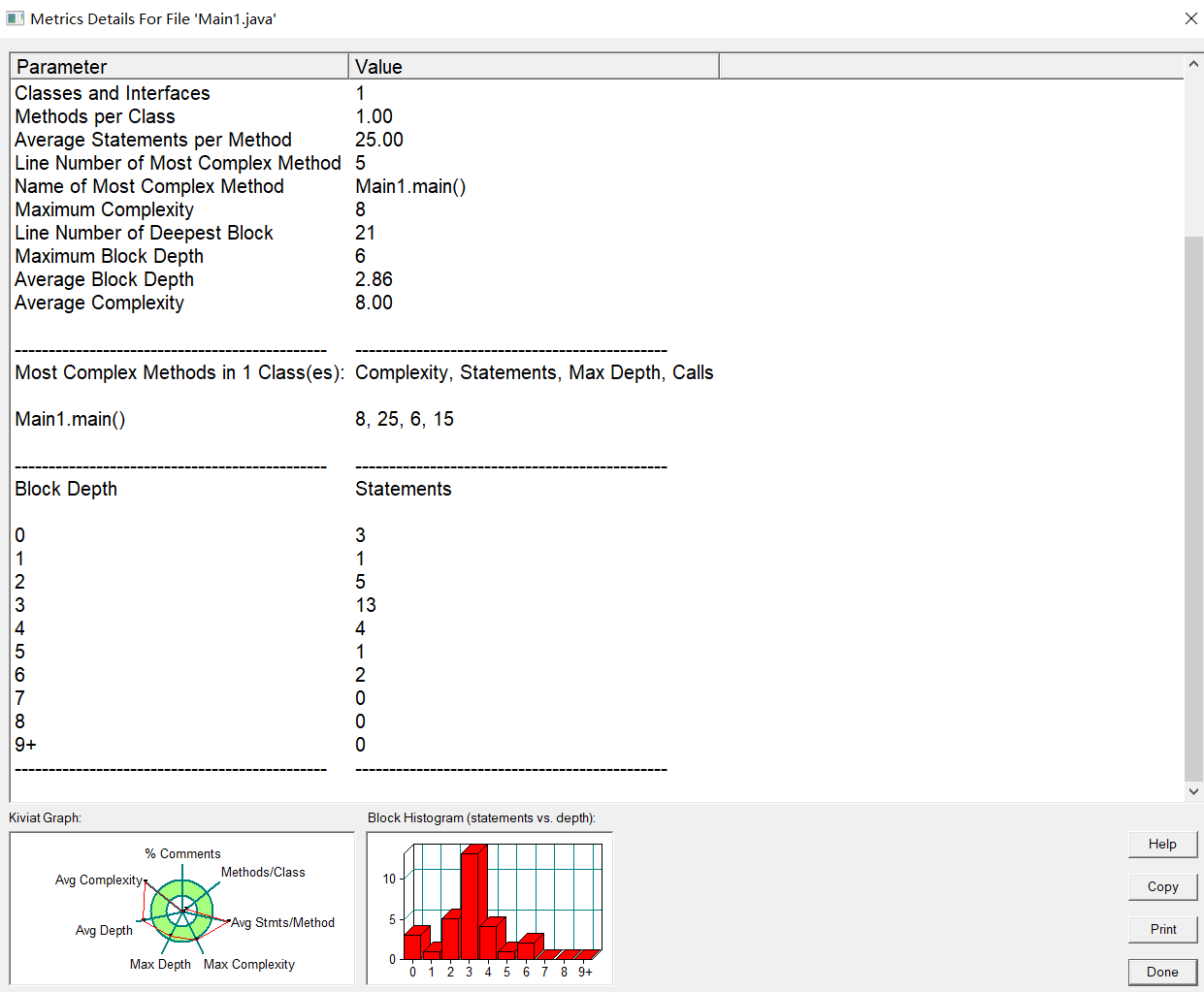
分析如下：
1.本题要求较为简单，只需要使用正则表达式筛选匹配字符串后，将得到的字符串转换回Double类型，再带进两点距离公式，即可得到结果，因此该代码复杂度较低，仅为8。
2.由于只使用了一个类来实现题目要求，类图中没有其他依赖，导致代码复用性比较低。
7-2 点线形系列2-线的计算
题目：
用户输入一组选项和数据，进行与直线有关的计算。选项包括：
1：输入两点坐标，计算斜率，若线条垂直于X轴，输出"Slope does not exist"。
2：输入三个点坐标，输出第一个点与另外两点连线的垂直距离。
3：输入三个点坐标，判断三个点是否在一条线上，输出true或者false。
4：输入四个点坐标，判断前两个点所构成的直线与后两点构成的直线是否平行，输出true或者false.
5：输入四个点坐标，计算输出前两个点所构成的直线与后两点构成的直线的交点坐标，x、y坐标之间以英文分隔","，并输出交叉点是否在两条线段之内（不含四个端点）的判断结果(true/false)，判断结果与坐标之间以一个英文空格分隔。若两条线平行，没有交叉点，则输出"is parallel lines,have no intersection point"。
输入格式：
基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
例如：1:0,0 1,1
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
不论哪个选项，如果格式、点数量都符合要求，但构成任一条线的两个点坐标重合，输出"points coincide"，
输出格式：
见题目描述。
代码展示：
package Third;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main2 {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
String s = sc.nextLine();
char c = s.charAt(0);
List<Double> list=new ArrayList<>();
if(s.length()<=2)
{
System.out.println("Wrong Format");
return;
}
if(s.charAt(1)!=':')
{
System.out.println("Wrong Format");
return;
}
int i = (int) c - '0';
if(!(i<=5&&i>=1))
{
System.out.println("Wrong Format");
return;
}
String split1 = s.split(":")[1];
String[] s1 = split1.split(" ");
for (String s2 : s1) {
String[] split = s2.split(",");
if(split.length!=2)
{
System.out.println("Wrong Format");
return;
}
for (String s3 : split) {
if(!s3.matches("^[+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?)"))
{
System.out.println("Wrong Format");
return;
}
else {
list.add(Double.parseDouble(s3));
}
}
}
switch (c)
{
case '1':{
if(s1.length!=2)
{
System.out.println("wrong number of points");
break;
}
if(list.get(0).equals(list.get(2))&&list.get(1).equals(list.get(3)))
{
System.out.println("points coincide");
return;
}
else if(list.get(2)-list.get(0)==0)
{
System.out.println("Slope does not exist");
return;
}
else {
double res=(list.get(3)-list.get(1))/(list.get(2)-list.get(0));
System.out.println(res);
}
break;
}
case '2':{
double A,B,C;
if(s1.length!=3)
{
System.out.println("wrong number of points");
}
else {
//先计算斜率
if(list.get(5).equals(list.get(3))&&list.get(4).equals(list.get(2)))
{
System.out.println("points coincide");
return;
}
A=list.get(5)-list.get(3);
B=list.get(2)-list.get(4);
C=list.get(4)*list.get(3)-list.get(5)*list.get(2);
double res=Math.abs((list.get(0)*A+list.get(1)*B+C)/(Math.sqrt(Math.pow(A,2)+Math.pow(B,2))));
System.out.println(res);
}
break;
}
case '3':{
if(s1.length!=3)
{
System.out.println("wrong number of points");
}
else {
if((list.get(0).equals(list.get(2))&&list.get(1).equals(list.get(3)))||(list.get(0).equals(list.get(4))&&list.get(1).equals(list.get(5)))||(list.get(4).equals(list.get(2))&&list.get(5).equals(list.get(3))))
{
System.out.println("points coincide");
return;
}
double slope1=(list.get(3)-list.get(1))/(list.get(2)-list.get(0));
double slope2=(list.get(5)-list.get(3))/(list.get(4)-list.get(2));
if(slope1==slope2)
{
System.out.println(true);
}
else {
System.out.println(false);
}
}
break;
}
case '4':{
if(s1.length!=4)
{
System.out.println("wrong number of points");
}
else
{
if((list.get(0).equals(list.get(2))&&list.get(1).equals(list.get(3)))||(list.get(4).equals(list.get(6))&&list.get(5).equals(list.get(7))))
{
System.out.println("points coincide");
return;
}
double slope1=(list.get(3)-list.get(1))/(list.get(2)-list.get(0));
double slope2=(list.get(7)-list.get(5))/(list.get(6)-list.get(4));
if(slope1!=slope2)
{
System.out.println(false);
}
else {
System.out.println(true);
}
}
break;
}
case '5':{
double A1,A2,B1,B2,C1,C2;
if(s1.length!=4)
{
System.out.println("wrong number of points");
}
else {
if((list.get(0).equals(list.get(2))&&list.get(1).equals(list.get(3)))||(list.get(4).equals(list.get(6))&&list.get(5).equals(list.get(7))))
{
System.out.println("points coincide");
return;
}
double slope1=(list.get(1)-list.get(3))/(list.get(0)-list.get(2));
double slope2=(list.get(5)-list.get(7))/(list.get(4)-list.get(6));
double x1,x2,x3,x4,y1,y2,y3,y4;
x1= list.get(0);
x2=list.get(2);
x3=list.get(4);
x4=list.get(6);
y1=list.get(1);
y2=list.get(3);
y3=list.get(5);
y4=list.get(7);
if(x1==x2)
{
if(x3==x4)
{
System.out.println("is parallel lines,have no intersection point");
return;
}
}
else if(x3!=x4)
{
if(slope1==slope2)
{
System.out.println("is parallel lines,have no intersection point");
return;
}
}
A1 = list.get(3)-list.get(1);
B1 = list.get(0)-list.get(2);
C1 = list.get(2)*list.get(1) -list.get(0)*list.get(3);
A2 = list.get(7)-list.get(5);
B2 =list.get(4)-list.get(6);
C2 = list.get(6)*list.get(5) -list.get(4)*list.get(7);
double x =((B2*C1-B1*C2) / (A2*B1-A1*B2));
double y = ((A1*C2-A2*C1) / (A2*B1-A1*B2));
if(((x-x1)*(x-x2))<0||((y-y1)*(y-y2))<0||((x-x3)*(x-x4))<0||((y-y3)*(y-y4))<0)
{
System.out.println(x+","+y+" "+true);
}
else
{
System.out.println(x+","+y+" "+false);
}
}
break;
}
}
}
}
类图如下：
SourceMonitor的代码分析图如下：
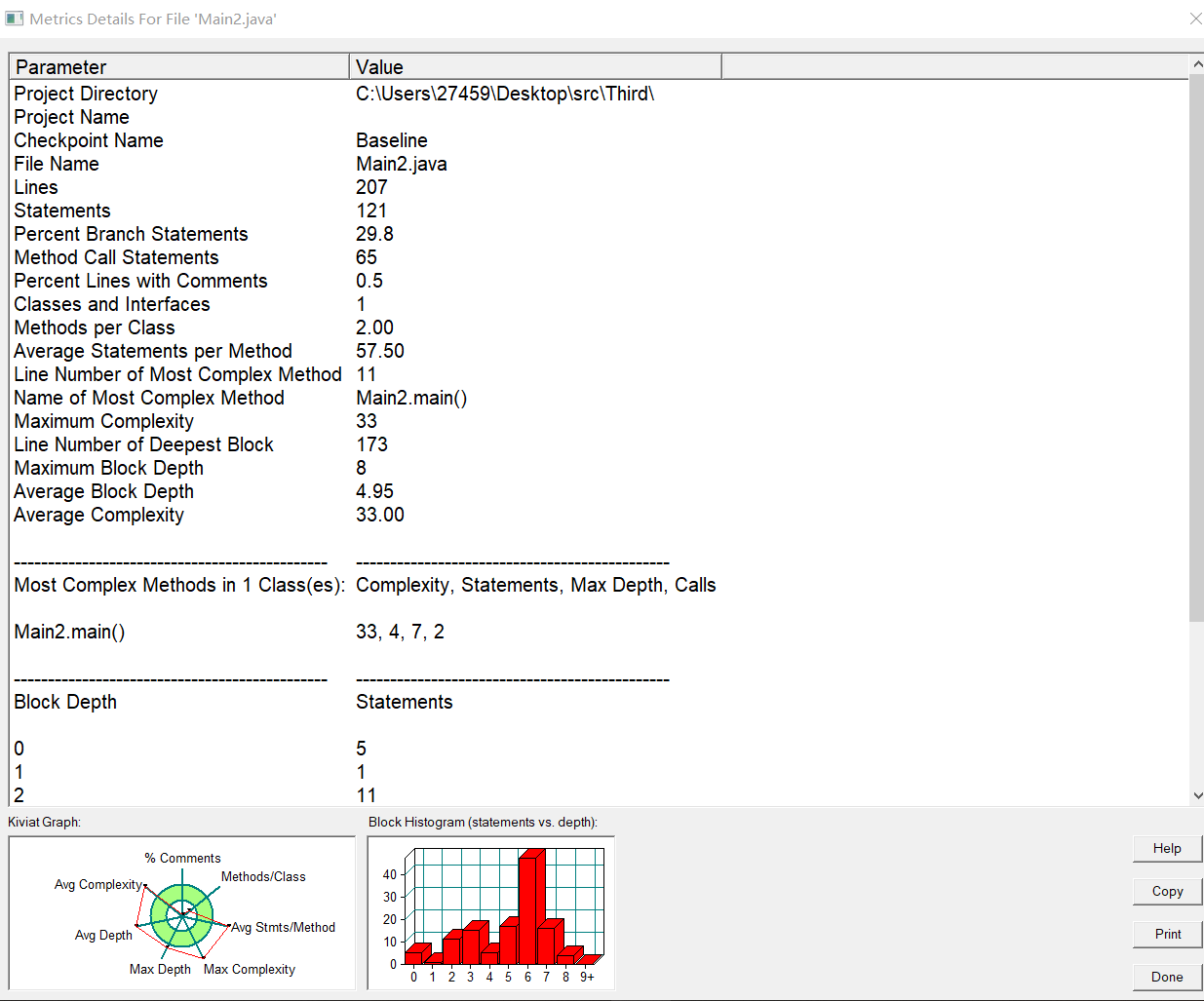
分析如下：
1.本题我没有提取出共同方法，导致环复杂度高达33，还没有达到理想情况。
2.本题我单独实现每个情况的解决方法，这导致代码的复用性较差。
7-3 点线形系列3-三角形的计算
题目：
用户输入一组选项和数据，进行与三角形有关的计算。选项包括：
1：输入三个点坐标，判断是否是等腰三角形、等边三角形，判断结果输出true/false，两个结果之间以一个英文空格符分隔。
2：输入三个点坐标，输出周长、面积、重心坐标，三个参数之间以一个英文空格分隔，坐标之间以英文","分隔。
3：输入三个点坐标，输出是钝角、直角还是锐角三角形，依次输出三个判断结果（true/false），以一个英文空格分隔，
4：输入五个点坐标，输出前两个点所在的直线与三个点所构成的三角形相交的交点数量，如果交点有两个，则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合，输出"The point is on the edge of the triangle"
5：输入四个点坐标，输出第一个是否在后三个点所构成的三角形的内部（输出in the triangle/outof triangle）。
必须使用射线法，原理：由第一个点往任一方向做一射线，射线与三角形的边的交点（不含点本身）数量如果为1，则在三角形内部。如果交点有两个或0个，则在三角形之外。若点在三角形的某条边上，输出"on the triangle"
输入格式：
基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。
输出格式：
基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
如果输入的三个点无法构成三角形，输出"data error"。
注意：输出的数据若小数点后超过6位，只保留小数点后6位，多余部分采用四舍五入规则进到最低位。小数点后若不足6位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333333，1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合，输出"points coincide"，
代码展示：
package Third;
import java.util.*;
public class Main3 {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
String s = sc.nextLine();
char cc = s.charAt(0);
int i = (int) cc - '0';
if(s.length()<=2)
{
System.out.println("Wrong Format");
return;
}
if(!(i<=5&&i>=1))
{
System.out.println("Wrong Format");
return;
}
if(s.charAt(1)!=':')
{
System.out.println("Wrong Format");
return;
}
String s1 = s.split(":")[1];
String[] s2 = s1.split(" ");
for (String s3 : s2) {
String[] split = s3.split(",");
if (split.length!=2)
{
System.out.println("Wrong Format");
return;
}
for (String s4 : split) {
if(!s4.matches("^[+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?)"))
{
System.out.println("Wrong Format");
return;
}
}
}
switch (cc)
{
case '1':{
if(s2.length!=3){
System.out.println("wrong number of points");
return;
}
point po=new point();
List<Double> list = po.getloaction(s1);
double x1,x2,x3,y1,y2,y3;
x1=list.get(0);
y1=list.get(1);
x2=list.get(2);
y2=list.get(3);
x3=list.get(4);
y3=list.get(5);
if(po.judge(x1,x2,x3,y1,y2,y3)==1)
{
System.out.println("data error");
return;
}
List<Double> length = po.getLength(s1);
if(length==null)
{
return;
}
double res1= length.get(0);
double res2= length.get(1);
double res3= length.get(2);
if(Math.abs(res1-res2)<0.1&&Math.abs(res2-res3)<0.1)
{
System.out.println(true+" "+true);
}
else if((Math.abs(res1-res2)<0.1||Math.abs(res2-res3)<0.1||Math.abs(res1-res3)<0.1))
{
System.out.println(true+" "+false);
}
else {
System.out.println(false+" "+false);
}
break;
}
case '2':{
point po=new point();
List<Double> list = po.getloaction(s1);
double x1,x2,x3,y1,y2,y3;
x1=list.get(0);
y1=list.get(1);
x2=list.get(2);
y2=list.get(3);
x3=list.get(4);
y3=list.get(5);
if(po.judge(x1,x2,x3,y1,y2,y3)==1)
{
System.out.println("data error");
return;
}
List<Double> temp=new ArrayList<>();
List<Double> length = po.getLength(s1);
List<String> result=new ArrayList<>();
if(s2.length!=3){
System.out.println("wrong number of points");
return;
}
if(length==null)
{
return;
}
double res1= length.get(0);
double res2= length.get(1);
double res3= length.get(2);
//计算周长
double len=res1+res2+res3;
//获得三个坐标位置
double p=len/2;
//获得面积
double era =Math.pow((p*(p-res1)*(p-res2)*(p-res3)),0.5);
double focus1=(x1+x2+x3)/3;
//重心x
double focus2=(y1+y2+y3)/3;
//重心y
temp.add(len);
temp.add(era);
temp.add(focus1);
temp.add(focus2);
for (Double aDouble : temp) {
String str=String.valueOf(aDouble);
String substring = str.substring(str.indexOf(".") + 1);
int str_len;
if(substring.length()>6)
{
str_len=6;
}else {
str_len=substring.length();
}
String formats="%."+str_len+"f";
String out=String.format(formats,aDouble);
result.add(out);
}
temp=new ArrayList<>();
for (String s3 : result) {
double v = Double.parseDouble(s3);
temp.add(v);
}
System.out.println(temp.get(0)+" "+temp.get(1)+" "+temp.get(2)+","+temp.get(3));
break;
}
case '3':{
point po=new point();
List<Double> list = po.getloaction(s1);
double x1,x2,x3,y1,y2,y3;
x1=list.get(0);
y1=list.get(1);
x2=list.get(2);
y2=list.get(3);
x3=list.get(4);
y3=list.get(5);
if(po.judge(x1,x2,x3,y1,y2,y3)==1)
{
System.out.println("data error");
return;
}
List<Double> temp=new ArrayList<>();
List<Double> length = po.getLength(s1);
List<String> result=new ArrayList<>();
if(length==null)
{
return;
}
if(s2.length!=3){
System.out.println("wrong number of points");
return;
}
length.sort(new Comparator<Double>() {
@Override
public int compare(Double o1, Double o2) {
if(o1-o2>0)
{
return -1;
}
else
{
return 1;
}
}
});
double res1= length.get(0);
double res2= length.get(1);
double res3= length.get(2);
if(Math.abs((Math.pow(res1,2)-Math.pow(res2,2)-Math.pow(res3,2)))<0.001){
System.out.println(false+" "+true+" "+false);
}
else if((Math.pow(res1,2)-Math.pow(res2,2)-Math.pow(res3,2))>0)
{
System.out.println(true+" "+false+" "+false);
}
else if(Math.pow(res1,2)-Math.pow(res2,2)-Math.pow(res3,2)<0){
System.out.println(false+" "+false+" "+true);
}
break;
}
case '4':{
if(s2.length!=5){
System.out.println("wrong number of points");
return;
}
point po=new point();
List<Double> loaction = po.getloaction(s1);
double x1,x2,x3,x4,x5,y1,y2,y3,y4,y5;
x1=loaction.get(0);
y1=loaction.get(1);
x2=loaction.get(2);
y2=loaction.get(3);
x3=loaction.get(4);
y3=loaction.get(5);
x4=loaction.get(6);
y4=loaction.get(7);
x5=loaction.get(8);
y5=loaction.get(9);
if(x1==x2&&y1==y2)
{
System.out.println("points coincide");
return;
}
if(po.judge(x3,x4,x5,y3,y4,y5)==1)
{
System.out.println("data error");
return;
}
if((po.judge(x3,x4,x1,y3,y4,y1)==1&&po.judge(x3,x4,x2,y3,y4,y2)==1)||(po.judge(x4,x5,x1,y4,y5,y1)==1&&po.judge(x4,x5,x2,y4,y5,y2)==1)||(po.judge(x3,x5,x1,y3,y5,y1)==1&&po.judge(x3,x5,x2,y3,y5,y2)==1))
{
System.out.println("The Third.point is on the edge of the triangle");
return;
}
//判断交点数量，获取截取面积
// 1.判断交点数量
List<Double> in1 = po.intersection(x1, y1, x2, y2, x3, y3, x4, y4);
List<Double> in2 = po.intersection(x1, y1, x2, y2, x3, y3, x5, y5);
List<Double> in3 = po.intersection(x1, y1, x2, y2, x4, y4, x5, y5);
// System.out.println(in1);
// System.out.println(in2);
// System.out.println(in3);
List<List<Double>> in4=new ArrayList<>();
//如果有效交点数量小于2，不需要计算面积，直接输出
boolean com1 = po.confirm(in1.get(0), in1.get(1), x3, y3, x4, y4);
boolean com2 = po.confirm(in2.get(0), in2.get(1), x3, y3, x5, y5);
boolean com3 = po.confirm(in3.get(0), in3.get(1), x4, y4, x5, y5);
// System.out.println(com1);
// System.out.println(com2);
// System.out.println(com3);
//将得到的坐标去重，加入list表中
//如果是三角形三点中的一个，直接加入表中
if((in1.get(0)==(x3)&&in1.get(1)==(y3))||(in1.get(0)==x4&&in1.get(1)==y4)||(in1.get(0)==x5&&in1.get(1)==y5))
{
if(in4.size()!=0)
{
int flag=0;
for (List<Double> doubles : in4) {
Double aDouble = doubles.get(0);
Double aDouble1 = doubles.get(1);
boolean b = (in1.get(0)-aDouble==0) && (in1.get(1)-aDouble1==0);
if(b)
{
flag=1;
break;
}
}
if(flag==0)
{
in4.add(in1);
}
}
else if (in4.size()==0) {
in4.add(in1);
}
}
if((in2.get(0)==x3&&in2.get(1)==y3)||(in2.get(0)==x4&&in2.get(1)==y4)||(in2.get(0)==x5&&in2.get(1)==y5))
{
if(in4.size()!=0)
{
int flag=0;
for (List<Double> doubles : in4) {
Double aDouble = doubles.get(0);
Double aDouble1 = doubles.get(1);
boolean b = (in2.get(0)-aDouble==0) && (in2.get(1)-aDouble1==0);
if(b)
{
flag=1;
break;
}
}
if(flag==0)
{
in4.add(in2);
}
}
else if (in4.size()==0) {
in4.add(in2);
}
}
if((in3.get(0)==x3&&in3.get(1)==y3)||(in3.get(0)==x4&&in3.get(1)==y4)||(in3.get(0)==x5&&in3.get(1)==y5))
{
if(in4.size()!=0)
{
int flag=0;
for (List<Double> doubles : in4) {
Double aDouble = doubles.get(0);
Double aDouble1 = doubles.get(1);
boolean b = (in3.get(0)-aDouble==0) && (in3.get(1)-aDouble1==0);
if(b)
{
flag=1;
break;
}
}
if(flag==0)
{
in4.add(in3);
}
}
else if (in4.size()==0){
in4.add(in3);
}
}
//否则，判断是否在三角形三条边内(不会包含端点)
if(com1)
{
in4.add(in1);
}
if(com2)
{
in4.add(in2);
}
if(com3)
{
in4.add(in3);
}
// System.out.println(in4);
if(in4.size()<2)
{
if(in4.size()==0)
{
System.out.println(0);
return;
}
else if(in4.size()==1)
{
System.out.println(1);
return;
}
}
//两交点的情况0
if(in4.size()==2){
// System.out.println(in4);
//判断三角形三点相对于线段的位置
int judge1 = po.judge(in4.get(0).get(0), in4.get(1).get(0), x3, in4.get(0).get(1), in4.get(1).get(1), y3);
int judge2 = po.judge(in4.get(0).get(0), in4.get(1).get(0), x4, in4.get(0).get(1), in4.get(1).get(1), y4);
int judge3 = po.judge(in4.get(0).get(0), in4.get(1).get(0), x5, in4.get(0).get(1), in4.get(1).get(1), y5);
double area= po.getEra(x3, y3, x4, y4, x5, y5);
// System.out.println("大三角形面积"+area);
List<Double> temp=new ArrayList<>();
List<String> result=new ArrayList<>();
//三角形三个点都没有存在于截线上
// System.out.println(judge1);
// System.out.println(judge2);
// System.out.println(judge3);
if(judge3!=1&&judge1!=1&&judge2!=1)
{
double era=0;
//说明第三点与截线组成三角形
if(judge1==judge2)
{
era = po.getEra(in4.get(0).get(0), in4.get(0).get(1), in4.get(1).get(0), in4.get(1).get(1), x5, y5);
}
//说明第二点与截线组成三角形
else if(judge1==judge3)
{
era = po.getEra(in4.get(0).get(0), in4.get(0).get(1), in4.get(1).get(0), in4.get(1).get(1), x4, y4);
}
//说明第一点与截线组成三角形
else if(judge2==judge3)
{
era = po.getEra(in4.get(0).get(0), in4.get(0).get(1), in4.get(1).get(0), in4.get(1).get(1), x3, y3);
}
double ear2 = area - era;
temp.add(era);
temp.add(ear2);
for (Double aDouble : temp) {
String str=String.valueOf(aDouble);
String substring = str.substring(str.indexOf(".") + 1);
int str_len;
if(substring.length()>6)
{
str_len=6;
}else {
str_len=substring.length();
}
String formats="%."+str_len+"f";
String out=String.format(formats,aDouble);
result.add(out);
}
if(ear2>era)
{
System.out.println(2+" "+Double.parseDouble(result.get(0))+" "+Double.parseDouble(result.get(1)));
}
else{
System.out.println(2+" "+Double.parseDouble(result.get(1))+" "+Double.parseDouble(result.get(0)));
}
}
//截线与三角形中一点相交
else if(judge3==1||judge1==1||judge2==1)
{
double era1=0;
if(judge1==1)
{
era1= po.getEra(in4.get(0).get(0), in4.get(0).get(1), in4.get(1).get(0), in4.get(1).get(1), x4, y4);
}
else if(judge2==1)
{
era1= po.getEra(in4.get(0).get(0), in4.get(0).get(1), in4.get(1).get(0), in4.get(1).get(1), x3, y3);
}
else if(judge3==1)
{
era1= po.getEra(in4.get(0).get(0), in4.get(0).get(1), in4.get(1).get(0), in4.get(1).get(1), x3, y3);
}
double ear2 = area - era1;
temp.add(era1);
temp.add(ear2);
for (Double aDouble : temp) {
String str=String.valueOf(aDouble);
String substring = str.substring(str.indexOf(".") + 1);
int str_len;
if(substring.length()>6)
{
str_len=6;
}else {
str_len=substring.length();
}
String formats="%."+str_len+"f";
String out=String.format(formats,aDouble);
result.add(out);
}
if(ear2>era1)
{
System.out.println(2+" "+Double.parseDouble(result.get(0))+" "+Double.parseDouble(result.get(1)));
}
else{
System.out.println(2+" "+Double.parseDouble(result.get(1))+" "+Double.parseDouble(result.get(0)));
}
}
}
break;
}
case '5':{
point po=new point();
if(s2.length!=4){
System.out.println("wrong number of points");
return;
}
List<Double> loaction = po.getloaction(s1);
double x1,x2,x3,x4,y1,y2,y3,y4;
x1=loaction.get(0);
y1=loaction.get(1);
x2=loaction.get(2);
y2=loaction.get(3);
x3=loaction.get(4);
y3=loaction.get(5);
x4=loaction.get(6);
y4=loaction.get(7);
if(po.judge(x2,x3,x4,y2,y3,y4)==1)
{
System.out.println("data error");
return;
}
if(x1==x2&&y1==y2||x1==x3&&y1==y3||x1==x4&y1==y4)
{
System.out.println("on the triangle");
return;
}
double Era = po.getEra(x2, y2, x3, y3, x4, y4);
double era1 = po.getEra(x1, y1, x3, y3, x4, y4);
double era2= po.getEra(x1, y1, x2, y2, x4, y4);
double era3= po.getEra(x1, y1, x2, y2, x3, y3);
if(Math.abs(era1+era2+era3)-Era>0.01)
{
System.out.println("outof the triangle");
return;
}
else
{
int judge1 = po.judge(x2, x3, x1, y2, y3, y1);
int judge2 = po.judge(x2, x4, x1, y2, y4, y1);
int judge3 = po.judge(x3, x4, x1, y3, y4, y1);
if(judge1==1||judge2==1||judge3==1)
{
System.out.println("on the triangle");
return;
}
else {
System.out.println("in the triangle");
return;
}
}
}
}
}
}
class point {
public List<Double> getloaction(String s)
{
List<Double> list=new ArrayList<>();
Scanner sc= new Scanner(System.in);
String[] splits =null;
splits=s.split(" ");
for (String split : splits) {
String[] split1 = split.split(",");
for (String s1 : split1) {
Double aDouble = Double.valueOf(s1);
list.add(aDouble);
}
}
return list;
}
public List<Double> getLength(String s)
{
List<Double> list=new ArrayList<>();
List<Double> getloaction = getloaction(s);
double a,b,c,d,e,f;
a=getloaction.get(0);
b=getloaction.get(1);
c=getloaction.get(2);
d=getloaction.get(3);
e=getloaction.get(4);
f=getloaction.get(5);
double res1;
double res2;
double res3;
res1=Math.sqrt(Math.pow((a-c),2)+Math.pow((b-d),2));
res2=Math.sqrt(Math.pow((a-e),2)+Math.pow((b-f),2));
res3=Math.sqrt(Math.pow((c-e),2)+Math.pow((d-f),2));
//返回边的长度
list.add(res1);
list.add(res2);
list.add(res3);
return list;
}
//判断三点是否共线
public static int judge(double x1,double x2,double x3,double y1,double y2,double y3){
double k1,b1,c1;
k1 = y2-y1;
b1 = x1-x2;
c1 = x2*y1-x1*y2;
if(k1*x3+b1*y3+c1==0){
return 1;
}
else{
if(k1*x3+b1*y3+c1<0){
return -1;
}
else{
return 0;
}
}
}
//返回交点坐标的集合
public List<Double> intersection(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4)
{
List<Double> list=new ArrayList<>();
double slope1=((y2-y1)/(x2-x1));
double slope2=((y4-y3)/(x4-x3));
if(x1==x2)
{
if(x3==x4)
{
double a=1145;
double b=9999;
list.add(a);
list.add(b);
return list;
}
}
else if(x3!=x4)
{
if(slope1==slope2)
{
double a=1145;
double b=9999;
list.add(a);
list.add(b);
return list;
}
}
double A1,B1,C1,A2,B2,C2;
A1 = y2-y1;
B1 = x1-x2;
C1 = x2*y1 -x1*y2;
A2 = y4-y3;
B2 = x3-x4;
C2 = x4*y3-x3*y4;
double x =((B2*C1-B1*C2) / (A2*B1-A1*B2));
double y = ((A1*C2-A2*C1) / (A2*B1-A1*B2));
list.add(x);
list.add(y);
return list;
}
//判断是否在三角形内，包含端点
public boolean confirm(double res1,double res2,double x3,double y3,double x4,double y4)
{
if(((res1-x3)*(res1-x4))<0||((res2-y3)*(res2-y4))<0)
{
return true;
}
else
{
return false;
}
}
public double getEra(double x3,double y3,double x4,double y4,double x5,double y5)
{
List<Double> lengths = getLengths(x3, y3, x4, y4, x5, y5);
double res1= lengths.get(0);
double res2= lengths.get(1);
double res3= lengths.get(2);
//计算周长
double len=res1+res2+res3;
//获得三个坐标位置
double p=len/2;
//获得面积
double era =Math.pow((p*(p-res1)*(p-res2)*(p-res3)),0.5);
return era;
}
public List<Double> getLengths(double a,double b,double c,double d,double e,double f)
{
List<Double> list=new ArrayList<>();
double res1;
double res2;
double res3;
res1=Math.sqrt(Math.pow((a-c),2)+Math.pow((b-d),2));
res2=Math.sqrt(Math.pow((a-e),2)+Math.pow((b-f),2));
res3=Math.sqrt(Math.pow((c-e),2)+Math.pow((d-f),2));
//返回边的长度
list.add(res1);
list.add(res2);
list.add(res3);
return list;
}
}
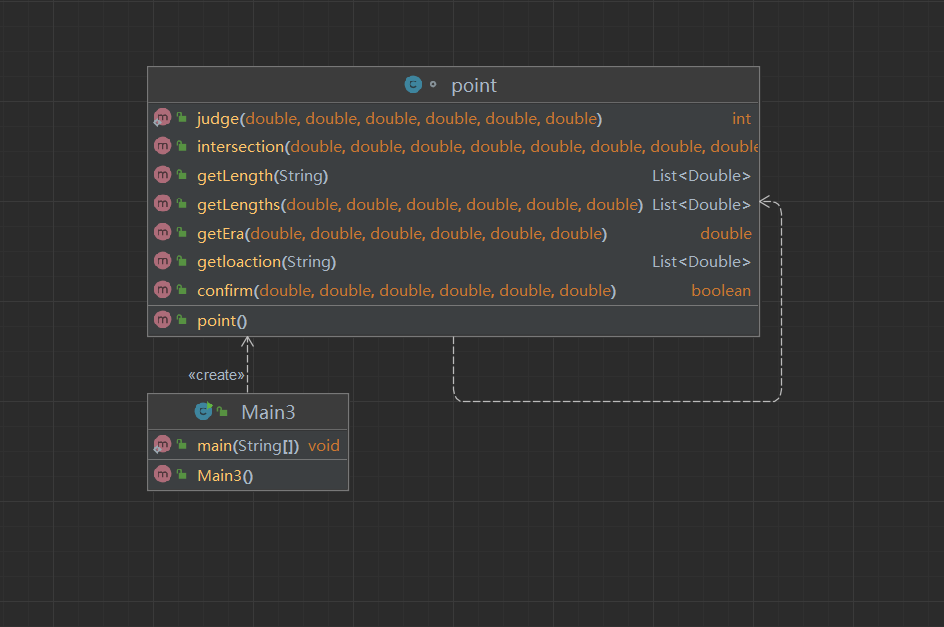
类图如下：
Sou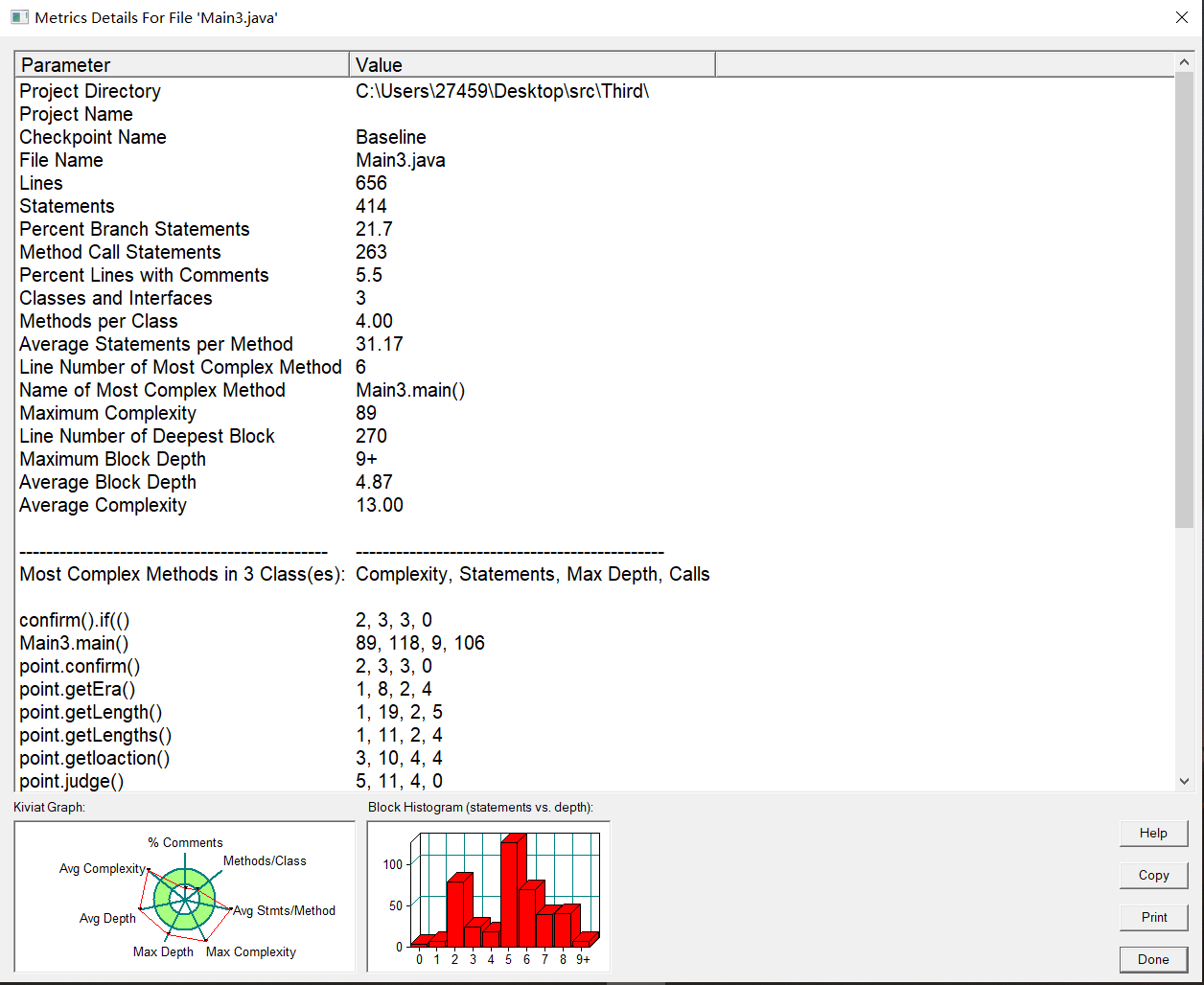
rceMonitor的代码分析图如下：
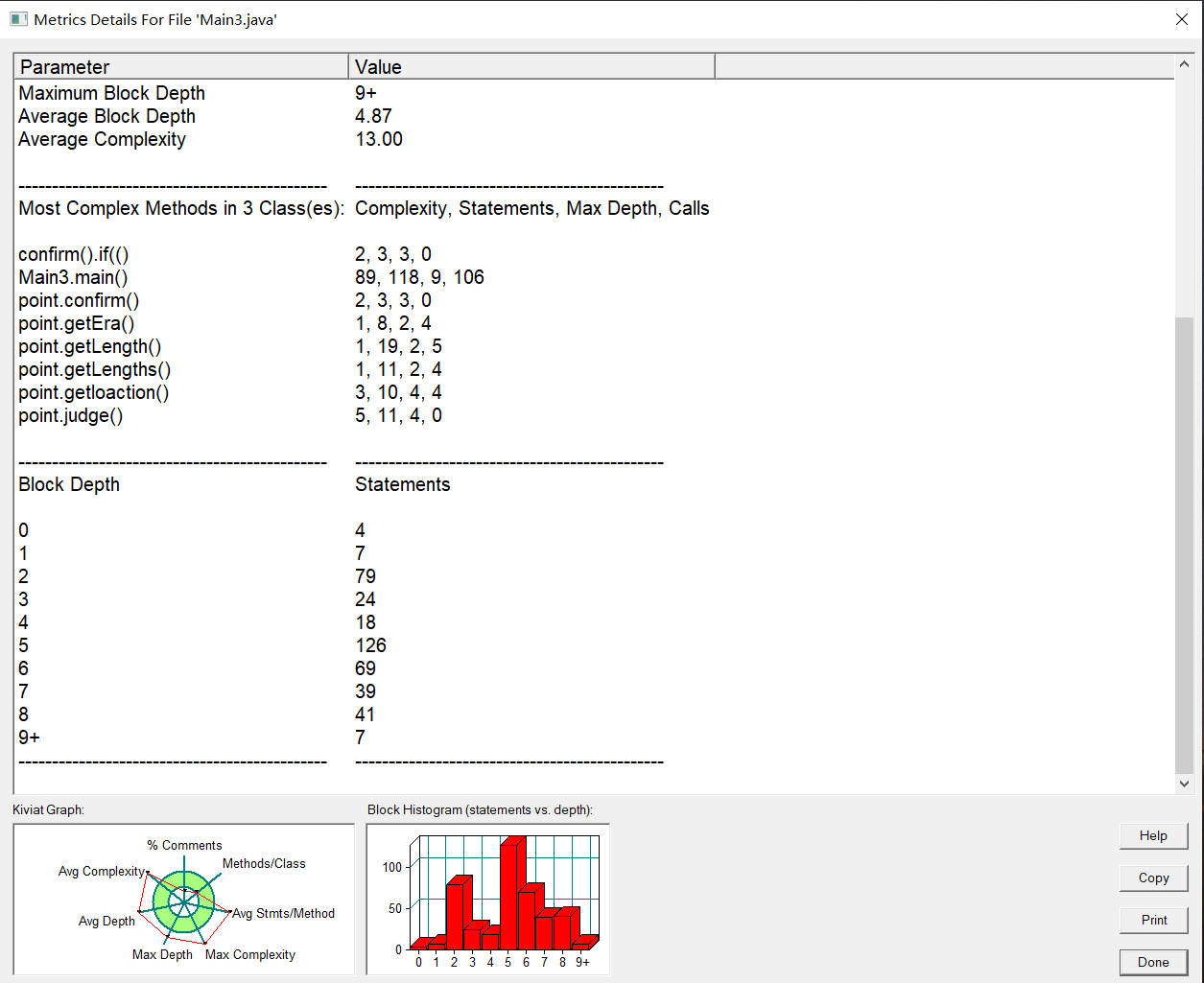
分析如下：
1.本题我是用了另一个类来实现点与点之间的基本操作，包括求两点间距离，求点与直线的距离，求两直线交点坐标等方法，导致代码复用性较好。
2.本次正则表达式可以沿用第二题的正则表达式，基本思想不变，主要是判断每个数字是否符合筛选情况，在进入Switch前先判断格式错误情况，防止格式判断错误。
3.由于情况4的算法判断较为复杂，导致我写了大量的if判断来实现不同情况的筛选，这导致环复杂度较高，希望之后能加以改进。
3.踩坑心得
第二次作业7-2 串口字符解析
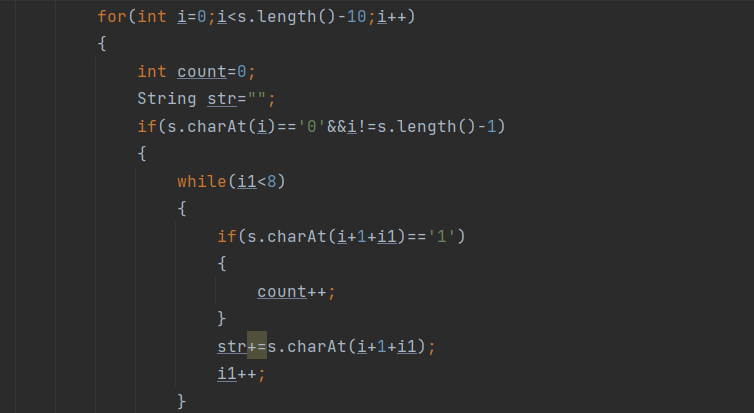
分析：由于要组成1次有效的数据至少需要11位数据，因此如果到了倒数第11位数字仍不为0，则接下来的10位不足以完成数据传输功能，退出循环。一开始编写代码时没有考虑这一问题，导致数组越界，增加跳出循环条件后，代码正常运行。
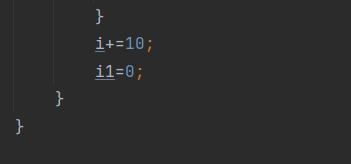
遍历字符串，每次递增10位，因为有可能存在两次有效数字间不存在空闲位的情况，一开始没有考虑到这种情况，导致测试点非0返回。
第三次作业 7-2 点线形系列2-线的计算
由于我使用List
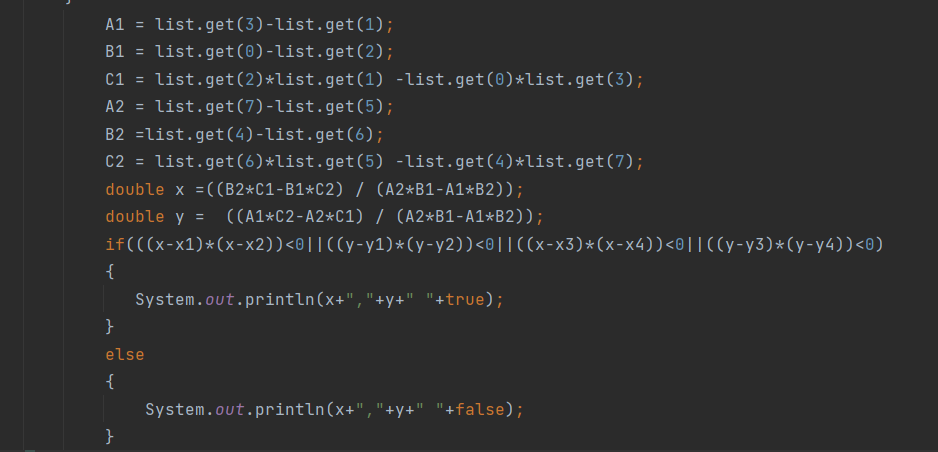
在情况5，判断点是否在线段内时，我一开始使用斜截式求得直线方程，结果由于精度问题，测试点无法通过，后来使用求直线一般式的方法得到直线方程，再判断点与直线两端的相对位置，成功通过测试点。
第三次作业 7-3 点线形系列3-三角形的计算
1.在情况4中，我先求三角形三条边的延伸直线与（x1,y1），（x2，y2）两点组成的直线的交点情况，先判断交点如果是三角形的三个顶点之一，则加入结果数组in4。
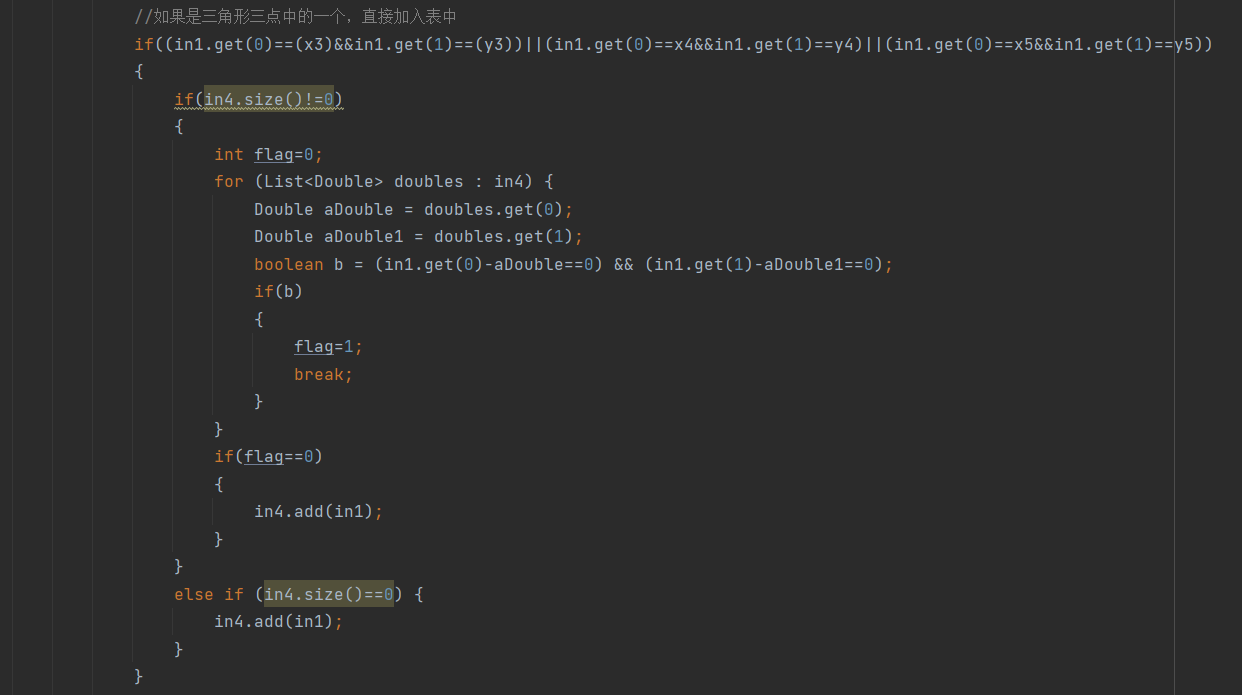
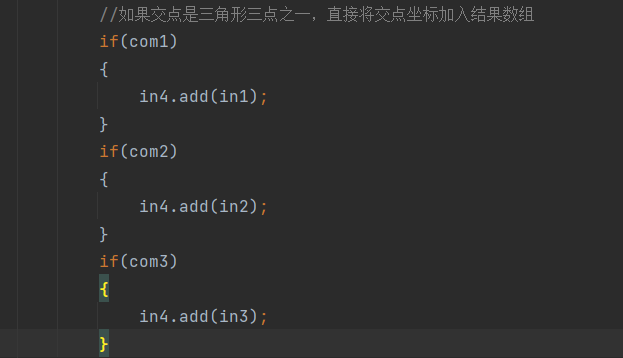
但是我忽略了前置直线有可能经过三角形中的一点，即有可能出现点重复的情况，这将导致后续取截线点时出现两个相同的点，最终导致判断出错，于是我增加了一个判断条件：如果直线与三角形三条边的交点不是三角形的顶点或者结果数组为空，则直接加入结果数组，否则，需要与结果数组已有元素进行对比，确保结果数组没有重复元素存在。
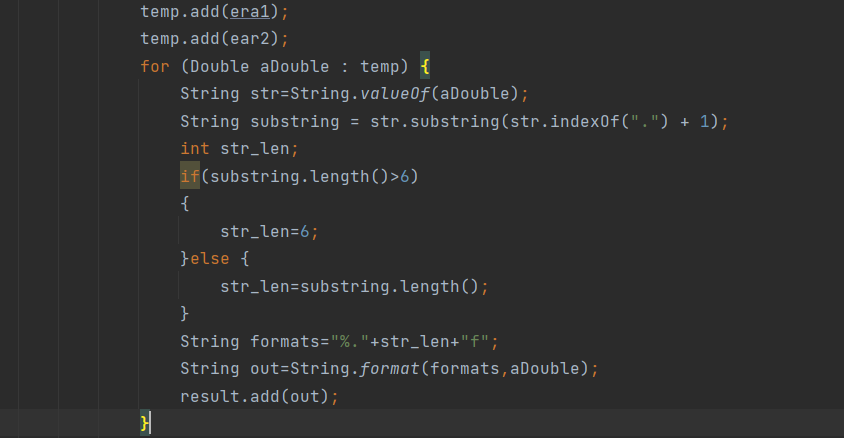
2.在四舍五入输出中，我发现结果有可能出现类似4.0000000000007这种数据结果，如果直接截取6位小数，用Stirng类型输出的话，会得到4.000000，后面多余的0将无法消去，于是我在使用String.format()得到初步转换结果后，再使用Double.parseDouble()将字符串转换回double类型数据，这样就可以避免小数点多余0位过多导致的结果错误问题。
4.代码改进建议
第二次作业 7-2 串口字符解析：将判断整合到工具类的对应方法中，以此增加代码复用性。
第三次作业 7-1 点线形系列1-计算两点之间的距离：可以增加工具类，在工具类方法中存储字符串截取结果，再将结果返回Main中。
第三次作业 7-2 点线形系列2-线的计算：提取公共方法例如计算两点距离，计算点线相对位置到工具类中，用以减少环复杂度和增强代码复用性。
第三次作业 7-3 在原有工具类Point上再进行拆分，将点与点的方法划如一个工具类Point，将点与线的方法划入工具类Point_Line,将线与线的方法划入工具类Line中，用以增强代码复用性。同时优化情况4，减少if判断，用以减少环复杂度。
5.作业总结
通过完成这三次PTA作业，我对字符串处理的基本方法有了更进一步的了解，也复习了正则表达式的基本使用方法。在编写Java代码的过程中，我注意到面向对象思想在优化代码结构，排除冗余代码块的方面所具有的巨大作用，在前期，我的代码仍然偏向于面向过程而非面向对象，这导致了代码的环复杂度相较于期望值更高，代码的复用性也不乐观，在第三次作业的第三题中，我增加了一个工具类来封装基本方法，这使得在主类中我通过调参，就能迅速地获得想要的结果，而非在每个方法中大量的复制粘贴之前写过的方法。虽然我之前就学习过Java，也了解后续的基本学习流程，可是完成本次作业依旧能提醒我注意在编写Java代码时应该时刻面向对象而非面向过程。希望在接下来image.png的学习过程中我能贯彻这一基本原则。
给老师的建议：希望题目能够更加专注于学习面向对象的基本原理，能在题目中体现Java的特性，而不是一昧追求极端测试样例。
