大数库GMP测试

一、任务详情

0. 在openEuler(推荐)或Ubuntu或Windows(不推荐)中完成下面任务
1. 用自己8位学号建两个文件夹xxxxxxxxsrc，xxxxxxxx，到GMP官网https://gmplib.org/下载最新代码到201x1xxxsrc，编译代码并把GMP库安装到201x1xxx文件夹。（5'）
2. 基于GMP的大数库编写测试代码测试大数运算，计算2的N次方，N为你学号的后四位（5‘）20
3. 基于GMP的大数库计算你以及前面5位同学和后面5位同学的8位学号的乘积（5‘）
4. 基于GMP的大数库编写测试代码测试大数运算，计算10000内的素数的乘积（5‘）
5. 提交代码（或代码链接）和运行结果截图

二、安装GMP

GMP 主要函数：https://www.shuzhiduo.com/A/WpdK7x2NdV/

sudo apt-get install m4  //默认没安装，gmp用这个
tar -jvxf gmp-6.2.1.tar.bz2    //解压
cd gmp-6.2.1
./configure --enable-cxx    //开启c++支持
make
make check   //注意必须检测一下，gmp官方特别提醒的
sudo make install

因为课前就完成了gmp下载，所以没有再次重新下载到20201212src和20201212学号文件夹里

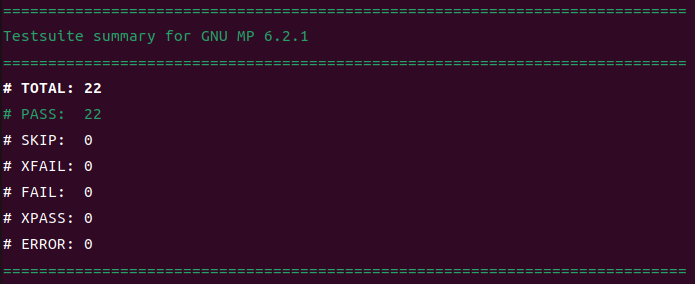
三、计算2的N次方，N为你学号的后四位

1.代码

#include<gmp.h>
#define N 1212
int main()
{
    mpz_t a,c;
    mpz_init(a);
    mpz_init(c);

    mpz_init_set_ui(a, 2);
    mpz_pow_ui(c, a, N);
    gmp_printf("2^%d = %Zd\n", N, c);

    mpz_clear(a);
    mpz_clear(c);
    return 0;
}

2.结果

2^1212 = 70526891853356034531603979043031594940743371757357833919419337999977433871326190057052096664518845125780975284354914663582043862183185043558365634079656826243725326219902938648103648856146145787520889095860455531443591926858713371483719982145691511131075312745428721576814913895557944855745498204068445694181321575408727502406563906376986273529501741633684526596096

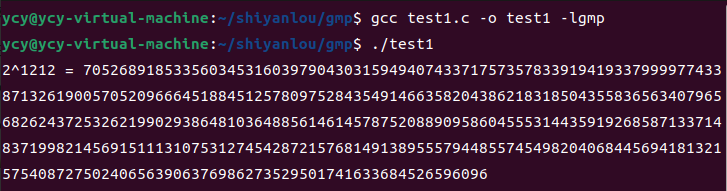
3.验证

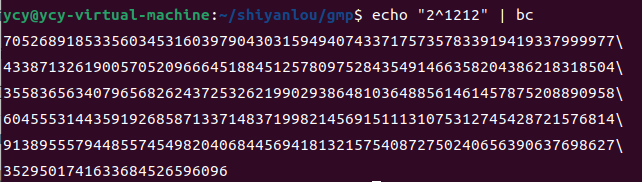
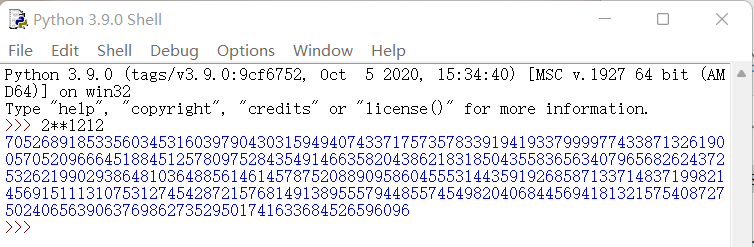
四、计算你以及前面5位同学和后面5位同学的8位学号的乘积

1.代码

#include<gmp.h>
#define N 20201212
int main()
{
    mpz_t a[11], b;
    mpz_init(b);
    mpz_init_set_str(b, "1", 10);

    const  char s[11][9]={"20201207","20201208","20201209","20201210","20201211","20201212","20201213","20201214","20201215","20201216","20201217"};
    int i;
    for(i=0;i<11;i++)
    {
         mpz_init(a[i]);
         mpz_init_set_str(a[i],s[i], 10);
         mpz_mul(b, b, a[i]);
    }

    gmp_printf("%d*%d*%d*%d*%d*%d*%d*%d*%d*%d*%d = \n%Zd\n", N-5, N-4, N-3, N-2, N-1, N, N+1, N+2, N+3, N+4, N+5, b);
    for(i=0;i<11;i++){
    	mpz_clear(a[i]);
    }

    mpz_clear(b);
    return 0;
}

2.结果

20201207×20201208×20201209×20201210×20201211×20201212×20201213×20201214×20201215×20201216×20201217 = 228639725305050118673387300827716832490277099781798350481341724181972362181836800

3.验证

五、基于GMP的大数库编写测试代码测试大数运算，计算10000内的素数的乘积

#include <stdio.h>
#include <stdlib.h>
#include <gmp.h>

int is_prime(mpz_t num)
{
    if (mpz_cmp_ui(num, 2) <= 0)
        return 0;
    else if (mpz_cmp_ui(num, 2) == 0)
        return 1;
    else if (mpz_even_p(num))
        return 0;
    else
    {
        mpz_t i,flag,temp;
        mpz_init(i);
        mpz_init(flag);
        mpz_init(temp);
        mpz_set_ui(i, 3);
        mpz_set_ui(temp, 2);
	mpz_cdiv_q (flag, num, temp);
        while (mpz_cmp(i, flag) <= 0)
        {
            if (mpz_divisible_p(num, i))
            {
                mpz_clear(i);
                return 0;
            }
            mpz_add_ui(i, i, 2);
        }

        mpz_clear(i);
        return 1;
    }
}

int main()
{
    int i;
    mpz_t result, num;
    mpz_init(result);
    mpz_init(num);

    mpz_set_ui(result, 1);

    for (i = 2; i < 10000; i++)
    {
        mpz_set_ui(num, i);
        if (is_prime(num))
            mpz_mul(result, result, num);
    }

    char *result_str = mpz_get_str(NULL, 10, result);
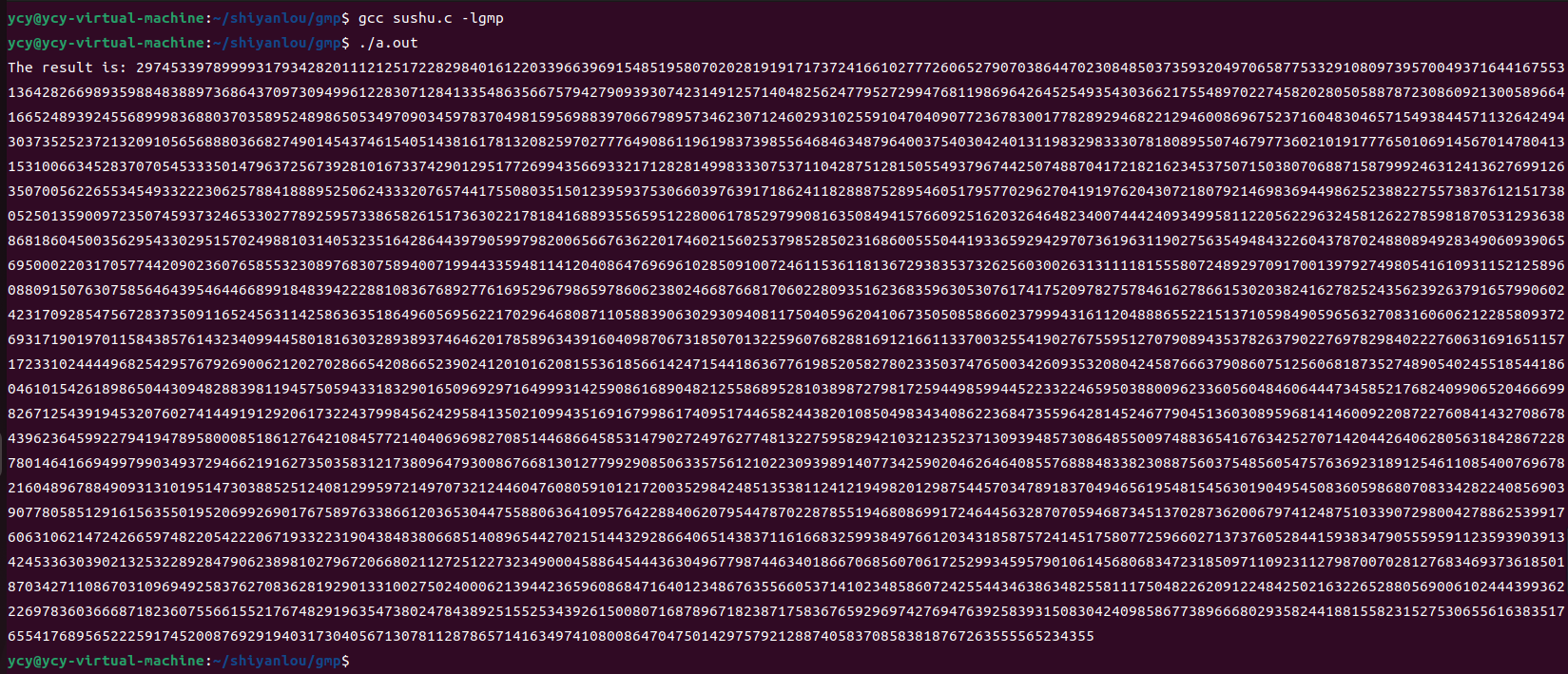
    printf("The result is: %s\n", result_str);

    mpz_clear(result);
    mpz_clear(num);
    free(result_str);

    return 0;
}