《安全编程技术》实验四 随机数生成算法实现及质量测试

一、实验目的与要求：

（一）实验目的

  该实验为设计性实验，实验目的如下：

1. 1. 学会如何采用软件方式设计和实现一个高质量的随机数生成算法。
   2. 掌握常用的随机数质量测试的方法。

（二）实验要求

1. 本实验一人一组，编程语言任选。
2. 要求学生掌握伪随机数的生成原理，了解常用的伪随机数生成算法，并熟练掌握所选的编程语言。
3. 要求学生能够设计一个伪随机数生成算法，并编程实现，具体要求如下：
   • 界面友好，操作方便。
   • 从界面输入需要生成的随机数个数和范围，并从界面输出生成的随机数（十六进制）。
   • 对生成的伪随机数进行统计检验。
4. 实验报告要求：
   • 实验报告要求包括实验目的、实验要求、实验内容（算法的设计）、实验结果（伪随机数质量）分析和实验体会等，重点在于实验内容（算法的设计）和实验结果（伪随机数质量）分析。实验报告要求上传和打印。
   • 理论联系实际，认真分析设计的伪随机数生成算法的优点和缺点。
   • 写出伪随机数生成算法设计和实现过程中的心得和体会，并回答实验中的思考题。
   • 实验报告撰写规范请见附。

 

二、实验内容、步骤及结论

（一）实验内容

1. 设计一个伪随机数生成算法。
2. 对（1）设计的伪随机数生成算法进行编程实现。
3. 对（2）产生的伪随机数进行统计检验

（二）线性同余法

  线性同余方法是目前应用广泛的伪随机数生成算法，其基本思想是通过对前一个数进行线性运算并取模从而得到下一个数。即：  a(i+1)=(a(i)*b+c)mod(m)

  其中b称为乘数，c称为增量，m称为模数，它们均为常数。

  乘数、增量和模数的选取可以多种多样，只要保证产生的随机数有较好的均匀性和随机性即可。

  线性同余法的最大周期是m，但一般情况下会小于m。要使周期达到最大，应该满足以下条件：

(1) c和m互质；

(2) m的所有质因子的积能整除b-1；

(3) 若m是4的倍数，则b-1也是；

(4) b，c，a(0)（初值，一般即种子）都比m小；

(5) b，c是正整数。

1.优势：

线性同余方法速度快，如果对乘数和模数进行适当的选择，可以满足用于评价一个随机数产生器的3 种准则：

(1)这个函数应该是一个完整周期的产生函数。也就是说，这个函数应该在重复之前产生出0 到m之间的所有数；

(2)产生的序列应该看起来是随机的；

(3)这个函数应该用32bit 算术高效实现。

2.不足：

线性同余法不具备不可预测性，因此不可以将线性同余法用于密码技术。

（三）代码

#include<stdio.h>
#include<math.h>
#include<time.h>

#define RANDOM_MAX 0x7FFFFFFF
#define NUM_MAX 10000
static unsigned long rand_seed;

void TenToSixteen(int num);		        //十进制转十六进制 
static long do_rand(unsigned long *value);
int myrand(void);
void mysrand(unsigned long seed);
void Math(int arr[],int len,int a,int b);	//计算平均值、方差、标准差 


int main() 
{
	int a,b,len,i;
	int arr[NUM_MAX];
	printf("请输入产生随机数数量:\n");
	scanf("%d",&len);
	printf("请输入产生随机数范围:\n");
	scanf("%d %d",&a,&b);
	printf("Output %d number between %d and %d:\n",len,a,b);
	mysrand (time (NULL));
	for (i = 0; i < len; i++){
		arr[i]=a+myrand()%(b-a+1);	//设范围区间为（max，min）,那么只需 rand%(max-min+1)+min 即可
		printf("第%d个数： ",i+1); 
		TenToSixteen(arr[i]);
	}
	Math(arr,len,a,b);
	return 0;
}

void TenToSixteen(int num)
{
        char arr[] = "0123456789ABCDEF";
        char hex[16];
        int i = 0;
        int j = 0;
        int a = 0;
        a = num;
        printf("%d ---> ",num);
        while (num)
        {
            hex[i++] = arr[num % 16];   //对十进制数求余并最终与hextable数组中的字符匹配
            num = num / 16;
        }
        printf("0x");
        for (j = i - 1; j >= 0; --j)
            printf("%c", hex[j]);
        printf("\n");
}

static long do_rand(unsigned long *value) {
	long quotient, remainder, t;

	quotient = *value / 127773L;
	remainder = *value % 127773L;
	t = 16807L * remainder - 2836L * quotient;
	if (t <= 0)
		t += 0x7FFFFFFFL;
	return ((*value = t) % ((unsigned long)RANDOM_MAX + 1));
}

int myrand(void) {
	return do_rand(&rand_seed);
}

void mysrand(unsigned long seed) {		//赋初值为种子
	rand_seed = seed;
}

void Math(int arr[],int len,int a,int b)
{
	int i,sum=0;
	int count[4];
	double average = 0;    //求平均数
	double var = 0;        //求方差
	double standard = 0;   //求标准差
	for(i=0;i<len;i++){
		sum+=arr[i];
	}
	average=sum*1.0/len;
	for(i=0;i<4;i++){
		count[i]=0;
	}
	for (i=0;i<len;i++)
    {
    	if(arr[i]<=average/2.0)
    		count[0]++;
    	else if(arr[i]>average/2.0 && arr[i]<=average)
    		count[1]++;
    	else if(arr[i]>average && arr[i]<=average*3.0/2.0)
    		count[2]++;
    	else
    		count[3]++;
        var += pow(arr[i]-average,2);
    }
    var=var/len; 
    standard = pow(var,0.5);//求标准差
    printf("\n平均数为  %.2f\n",average);
    printf("处于 %d — %.2f 之间的数有%d个\n",a,average/2.0,count[0]);
    printf("处于 %.2f — %.2f 之间的数有%d个\n",average/2.0,average*3.0/2.0,count[1]);
    printf("处于 %.2f — %.2f 之间的数有%d个\n",average,average*3.0/2.0,count[2]);
    printf("处于 %.2f — %d 之间的数有%d个\n",average*3.0/2.0,b,count[3]);
    printf("方差为    %.2f\n",var);
    printf("标准差为  %.2f\n",standard);
}

（四）运行

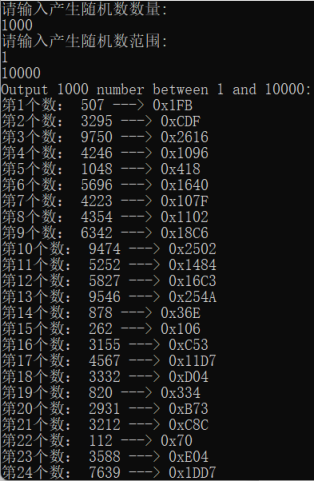
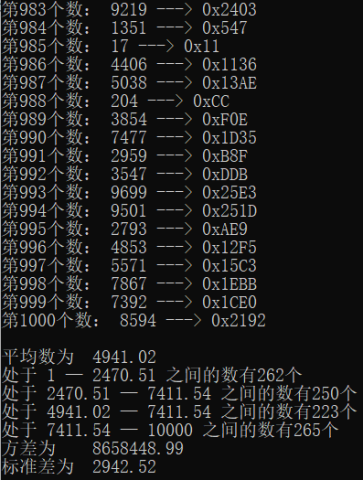
（五）性能分析

1. 参数检验（包括均值、方差或各阶距）

  产生的随机数方差和标准差较大，说明数据分散。

2. 随机数的均匀性

  产生的随机数平均分布在4个区间内，说明具有均匀性。

 

三、实验体会

除了你在实验中所用的方法，对伪随机数进行质量测试的方法还有哪些？

1. 可以利用matlab绘制点阵图观察均匀性、规律性、随机性。
2. 均匀性检验（包括卡方、柯氏和序列检验）
3. 独立性检验（包括相关系数、列联表和游程检验）