常见边缘检测算子极其实现(基于Python和OpenCV)

1.边缘检测类型和基本原理

在图像处理中，图像边缘常包括三种模型

1).台阶模型：相邻两个像素的灰度值快速变化；如：在离散灰度图像中，灰度值为...0,0,255,255,...就可视为台阶模型；

2).斜坡模型：图像中从亮到暗（或暗到亮）呈现一个类似于斜坡，如在离散灰度图像灰度：...,0,50,100,150,200,255,255...;

3).屋顶模型：...0,0,80,160,255,160,80,0,0,0...

如下图所示

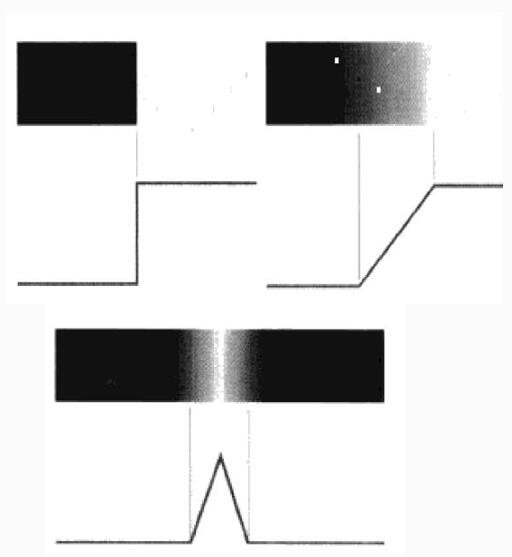
基本原理

边缘检测简单来说，就是对图像进行按模板进行卷积；边缘在图像上一般就表示为明暗交接的地方，从上面的图中看出，若我们将图像看为一个连续可导的函数，那么，对边缘检测，就是求突变的位置，在数学上，我们对这样连续可导图像是通过求导，因此，边缘也是通过同样的原理。但由于图像是离散矩阵形式，求导采用微分的形式。边缘检测中常见的数学方法如下图所示

2.常见的边缘检测算子

2.1Roberts算子

当对对角线方向的边缘感兴趣时，需要一个二维模板，Roberts交叉梯度算子是最早尝试使用这样的具有对角优势的二维算子，具体的函数实现如下

    #传入灰度图像
    #返回处理后图像
    def robert(self,img):
        #获取边界模板
        roberX=roberY=np.zeros((2,2))
        roberX[0][0]=-1;roberX[1][1]=1
        roberY[0][1]=-1;roberY[1][0]=1
        #计算图像大小
        m,n=np.shape(img)
        gx=0
        gy=0
        M=img[:]
        for i in range(m):
            for j in range(n):
                gx=np.sum(img[i:i+2,j:j+2]*roberX)
                gy=np.sum(img[i:i+2,j:j+2]*roberY)
                M[i][j]=abs(gx)+abs(gy)
        return M

2.2Prewitt算子

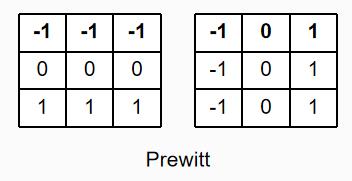
    #传入灰度图像
    #返回处理后图像
    def prewitt(self,img):
        prewitX=[[-1,-1,-1],
                 [0,0,0],
                 [1,1,1]]
        prewitY=[[-1,0,1],
                 [-1,0,1],
                 [-1,0,1]]
        m,n=np.shape(img)
        M=img[:]
        gx=0
        gy=0
        for i in range(m-3):
            for j in range(n-3):
                gx=np.sum(img[i:i+3,j:j+3]*prewitX)
                gy=np.sum(img[i:i+3,j:j+3]*prewitY)
                M[i][j]=abs(gx)+abs(gy)
        return M

2.3Sobel算子

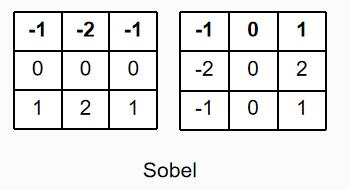
可以看出两个算子计算相差并不大，

    #传入灰度图像
    #返回处理后图像
    def sobel(self,img):
        #计算边界模板
        sobelX=np.array([[-1,-2,-1],
            [0,0,0],
            [1,2,1]])
        sobelY=np.array([[-1,0,1],
                          [-2,0,2],
                          [-1,0,1]])
        m,n=np.shape(img)
        gx=0
        gy=0
        #初始化与原图像相同数组
        M=np.zeros_like(img)
        for i in range(1,m-1):
            for j in range(1,n-1):
                gx=np.sum(img[i-1:i+2,j-1:j+2]*sobelX)
                gy=np.sum(img[i-1:i+2,j-1:j+2]*sobelY)
                M[i][j]=abs(gx)+abs(gy)
        return M

3.LOG算子

LOG边缘检测步骤：

1.先用n*n的高斯进行平滑处理；

2.对平滑后的图像再使用拉普拉斯算子进行边缘检测；

3.再找出图像的零交叉点，进行边界连接。

传统的边缘检测算法，实质就是一些模板（又称为算子）在图像上滑动，LOG算子也不例外，其模板计算公式如下图所示：

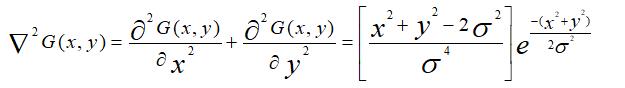
对于参数δ是要输入的参数，因此，对于模板大小n>=6δ原则，以上函数图像如下，因长的像草帽，又叫墨西哥草帽算子。

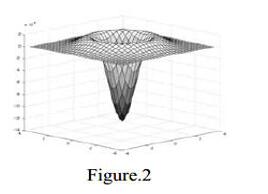
图像零交叉点的查找是该方法的核心部分之一，从上述公式可以看出，这是对原始图像进行二阶导数处理过程。若我们考虑上面提到的边缘检测的斜坡模型，求导数的图像如下所示

最左边的为原始图像，中间部分为一阶导数图像，经过一阶导后，斜坡部分为一个常数，最右边为二级求导后图像，二阶处理后斜坡部分变为0，但其进入斜坡的两个端点处，却不为零，而且方向相反（一正一负）。变化部分如图像中箭头所示。因此。我们可以基于该原理，进行边界提取。即通过3*3模板进行边界查找，判断经过上面模板处理后图像为0像素的上下、左右，两个对角4个方向是否相反，若相反，则标记为边缘。对于台阶模型边缘只需其上下、左右4个方向上符号相反即可。

#MarrHildreth边界检测
class marrHildreth():
    def edgesMarrHildreth(self,img,sigma):
        #动态确定滤波器大小，大于6sigma的奇数
        size=int(2*(np.ceil(3*sigma))+1)
        x,y=np.meshgrid(np.arange(-size/2-1,size/2+1),np.arange(-size/2-1,size/2+1))
        # normal=1/(2.0*np.pi*sigma**2)
        #计算LoG滤波器
        kernel=((x**2+y**2-(2.0*sigma**2))/sigma**4)*np.exp(-(x**2+y**2)/(2.0*sigma**2))
        kern_size=kernel.shape[0]

        m,n=np.shape(img)
        log=np.zeros_like(img,dtype=float)

        t=int(kern_size/2)#定义起始点

        for i in range(t,m-t):
            for j in range(t,n-t):
                window=img[i-t:i+(t+1),j-t:j+(t+1)]*kernel
                log[i,j]=np.sum(window)
        log=log.astype(np.int64,copy=False)
        zero_crossing=np.zeros_like(log)
        #寻找零交叉点
        for i in range(1,log.shape[0]-1):
            for j in range(1,log.shape[1]-1):
                #斜坡型，使用3*3模板，零交叉点处，至少相邻俩个方向二阶导数符号相反，
                #上/下；左/右，两个对角方向
                if log[i][j]==0:
                    if(log[i][j-1] < 0 and log[i][j+1] > 0) \
                            or (log[i][j-1] > 0 and log[i][j+1] < 0) \
                            or (log[i-1][j] < 0 and log[i+1][j] > 0) \
                            or (log[i-1][j] > 0 and log[i+1][j] < 0) \
                            or ((log[i - 1][i - 1] > 0) and (log[i + 1][j + 1] < 0)) \
                            or ((log[i - 1][i - 1] < 0) and (log[i + 1][j + 1] > 0)):
                        zero_crossing[i][j]=255
                #阶梯型，只要两个相邻（4领域）中符号相反
                if log[i][j]<0:
                    if(log[i][j-1]>0)or(log[i][j+1]>0)or(log[i-1][j]>0)or(log[i+1][j]>0):
                        zero_crossing[i][j]=255
        return zero_crossing

可以看出LOG结果并不理想，这应该是程序设计有问题！

4.Canny算子，最经典的一种算子之一

基本步骤

1.用二维高斯平滑图像；由于二维高斯过程计算比较复杂，通常可以将其近似看为沿x，y两个方向上计算；

2.计算图像梯度；

3.非最大抑制；

4.双阈值进行边界提取

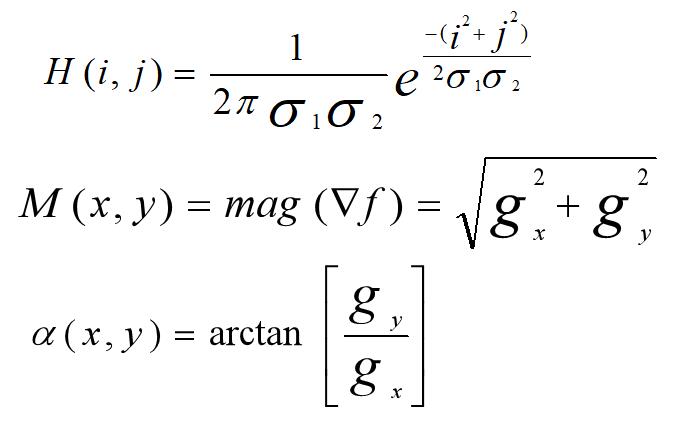
高斯平滑、计算梯度和角度的公式如上所示。这里还有一个重要的性质是梯度的方向和边缘的方向相互垂直。

    #将RGB图像转化为灰度图像
    def gray(self,img_path):
        img=plt.imread(img_path)
        img_rgb=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
        img_gray=np.dot(img_rgb[...,:3],[0.299,0.587,0.114])
        return img_gray

    #高斯滤波平滑图像
    def smooth(self,img_gray,sigmal1=1.4,sigmal2=1.4):
        sigmal1=sigmal1
        sigmal2=sigmal2
        gau_sum=0
        gaussian=np.zeros([5,5])
        for i in range(5):
            for j in range(5):
                gaussian[i,j]=math.exp((-1/(2*sigmal2*sigmal1))*(np.square(i-3)+
                                                               np.square(j-3)))/(2*math.pi*sigmal1*sigmal2)
                gau_sum=gau_sum+gaussian[i,j]
            gaussian=gaussian/gau_sum
            W,H=img_gray.shape
            new_gray=np.zeros([W-5,H-5])
            for i in range(W-5):
                for j in range(H-5):
                    new_gray[i,j]=np.sum(img_gray[i:i+5,j:j+5]*gaussian)
        return new_gray
    #计算dx,dy,M,thana
    def gradients(self,new_gray):
        W,H=new_gray.shape
        dx=np.zeros([W-1,H-1])
        dy=np.ones([W-1,H-1])
        M=np.zeros([W-1,H-1])
        theta=np.zeros([W-1,H-1])
        for i in range(W-1):
            for j in range(H-1):
                dx[i,j]=new_gray[i+1,j]-new_gray[i,j]
                dy[i,j]=new_gray[i,j+1]-new_gray[i,j]
                M[i,j]=np.sqrt(np.square(dx[i,j])+np.square(dy[i,j]))
                theta[i,j]=math.atan(dx[i,j]/(dy[i,j]+0.0000001))
        return dx,dy,M,theta

非最大值抑制：

核心：梯度是有方向矢量，通常在进行非最大抑制时使用3*3模板进行查找该方向线上的两个向量，要求给定像元梯度要大于这两个方向线上的梯度值。

下面介绍两种非最大值抑制的方法

1)基于灰度图像插值的方法

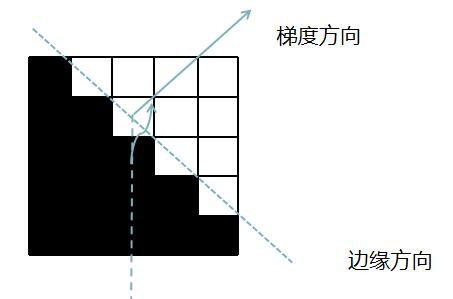
从上图中可以看到，如前面介绍，梯度方向与边缘相互垂直，即，图中短线代表边缘，长的带箭头的表示梯度方向，在图中所示，上面部分在b中，但离a较近；下面部分在g中，但其离h较近，这时，我们不能简单的将上面部分看为b，下半部视为g，因该通过插值的方法通过a、b计算上面部分值，同样通过下半部分g、h计算下面值。

 

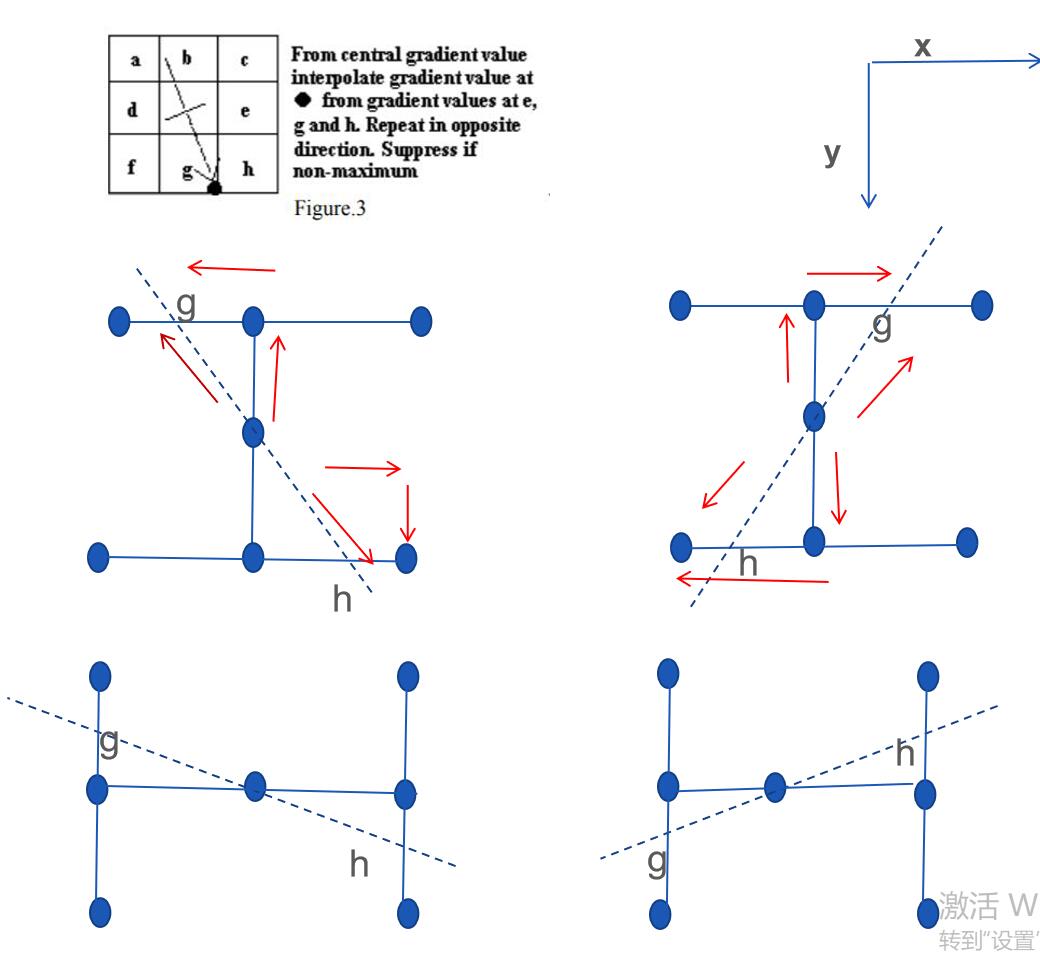
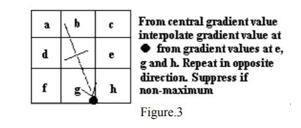
将以上过程简化为上图所示，图中虚线代表梯度方向，中间两个图均有一个共同的性质，即沿y轴方向导数大于沿x轴方向导数。同理，最下面两个图沿x轴方向导数大于沿y方向导数。首先我们要明确我们的目标是插值计算出图中g,h值。以中间的两个图为例，前面介绍了中间两个图沿y轴方向导数大于x轴；那么我们就可以明确在该条件下首先可以获取到上下两个值。之后还要进一步判断，中间两个图中左图：两个方向（x,y）上的梯度相乘大于0（判断方法：梯度有方向，首先假设梯度方向，再看x、y方向）；中间两个图中右图，两个方向相乘小于零。这样就可以判断出要进行插值的另外两个点。

    #非最大抑制方案2
    def NMS(self,M,dx,dy):
        #M:梯度
        #dx:x方向导数
        #dy:y方向导数
        d=np.copy(M)
        W,H=M.shape
        NMS=np.zeros((W,H))
        NMS[0,:]=NMS[W-1,:]=NMS[:,0]=NMS[:,H-1]=0
        for i in range(1,W-1):
            for j in range(1,H-1):
                #找到可能边缘点
                if M[i,j]!=0:
                    #x方向导数
                    gradx=dx[i,j]
                    #y方向导数
                    grady=dy[i,j]
                    #当前梯度
                    gradTemp=M[i,j]
                    #如果 x 方向梯度值比较大，说明导数方向趋向于 x 分量
                    if np.abs(gradx)>np.abs(grady):
                        #权重
                        weight=np.abs(grady)/np.abs(gradx)
                        grad2=M[i-1,j]
                        grad4=M[i+1,j]
                        if gradx*grady>0:
                            # 如果 x, y 方向导数符号一致
                            # 像素点位置关系
                            # g1
                            # g2  c  g4
                            #        g3
                            grad1=M[i-1,j-1]
                            grad3=M[i+1,j+1]
                        else:
                            # 如果 x，y 方向导数符号相反
                            # 像素点位置关系
                            #        g3
                            # g2  c  g4
                            # g1
                            grad1=M[i-1,j+1]
                            grad3=M[i+1,j-1]
                    else:
                        weight=np.abs(gradx)/np.abs(grady)
                        grad2=M[i,j-1]
                        grad4=M[i,j+1]
                        # 如果 x, y 方向导数符号相反
                        # 像素点位置关系
                        #    g2 g1
                        #    c
                        # g3 g4
                        if gradx*grady<0:
                            grad1=M[i+1,j-1]
                            grad3=M[i-1,j+1]
                        # 如果 x，y 方向导数符号一致
                        # 像素点位置关系
                        # g1 g2
                        #    c
                        #    g4  g3
                        else:
                            grad1=M[i-1,j-1]
                            grad3=M[i+1,j+1]
                    #分别计算两个方向的灰度差值
                    gradTemp1=weight*grad2+(1-weight)*grad1
                    gradTemp2=weight*grad4+(1-weight)*grad3
                    #若该梯度均大于差值的灰度值，则保留，否则赋值为零，抑制
                    if gradTemp>=gradTemp1 and gradTemp>=gradTemp2:
                        NMS[i,j]=gradTemp
        return NMS

2)基于角度非最大值抑制方法

前面提到图像边界与梯度方向相互垂直。

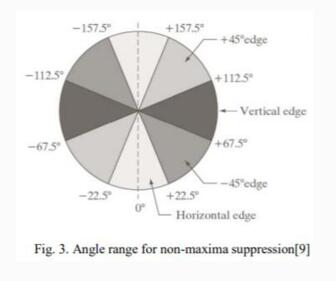
基本流程：

1).令d1、d2、d3、d4分别表示水平、垂直、-45°、+45°角度范围。

2).同样采用3*3模板进行非极大值抑制，但现在使用的是角度。

3).首先根据角度判断是在什么方向。

4).中间像素要大于相邻俩个方向上的值。

    #非最大抑制方案1
    def NMS1(self,M,dx,dy,theta):
        #定义常数，将弧度转化为度
        gree=180.0/math.pi
        W,H=np.shape(M)
        #获取角度值
        d = np.copy(theta)
        NMS=np.zeros((W,H))
        NMS[0,:]=NMS[W-1,:]=NMS[:,0]=NMS[:,H-1]=0
        for i in range(1,W-1):
            for j in range(1,H-1):
                if M[i,j]!=0:
                    gradTemp=d[i][j]*gree
                    #水平边缘
                    if((-157.5<=gradTemp<=157.5) or (-22.5<=gradTemp<=22.5)):
                        if(M[i][j]>M[i-1][j] and M[i][j]>M[i+1][j]):
                            NMS[i][j]=M[i][j]
                    #45°边缘
                    if((112.5<=gradTemp<=157.5) or (-67.5<=gradTemp<=-22.5)):
                        if(M[i][j]>M[i+1][j-1] and(M[i][j]>M[i-1][j+1])):
                            NMS[i][j]=M[i][j]
                    #垂直边缘
                    if((-112.5<=gradTemp<=-67.5) or (67.5<=gradTemp<=122.5)):
                        if(M[i][j]>M[i-1][j]and(M[i][j]>M[i][j+1])):
                            NMS[i][j]=M[i][j]
                    #-45°边缘
                    if((-157.5<=gradTemp<=112.5) or (22.5<=gradTemp<=67.5)):
                        if(M[i][j]>M[i-1][j-1]and(M[i][j]>M[i+1][j+1])):
                            NMS[i][j]=M[i][j]
        return NMS

双阈值边界提取

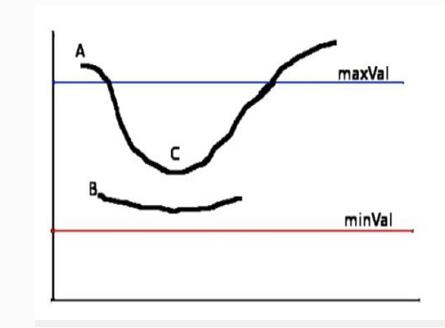
1).Canny算子采用的是高低俩个阈值来进行边界连接，通常高低阈值取值比为2:1或3:1，即TH:TL=2:1(或3:1);

2).高于TH高阈值的点认为是边界点，而低于低阈值点认为不可能为边界点，

3).高于低阈值，低于高阈值间的点，要进行判断（这里采用3*3模板）在该点的8个邻域中是否有高于高阈值(TH)点，若有，则将该点视为边界点

#双阈值处理
    def double_threshold(self,NMS):
        W,H=NMS.shape
        DT=np.zeros([W,H])
        #高低阈值比为：1：3
        TL=0.1*np.max(NMS)
        TH=0.3*np.max(NMS)

        for i in range(1,W-1):
            for j in range(1,H-1):
                #将低于最小阈值都设为0
                if(NMS[i,j]<TL):
                    DT[i,j]=0
                #将大于最高阈值都设为1
                elif(NMS[i,j]>=TH):
                    DT[i,j]=255

                #用8连通方法得到高低阈值间的边缘像素
                elif((NMS[i-1,:]>=TH).any()) or ((NMS[i+1,:]>=TH).any()) or ((NMS[i,[j-1,j+1]]>=TH).any()):
                    DT[i,j]=255
                # elif((NMS[i-1,[j-1,j+1]>TH].any())or((NMS[i+1,[j-1,j+1]]>TH).any())or((NMS[i,[j-1,j+1]]>TH).any())):
                #     DT[i,j]=255
        return DT

Canny算子总代码

#Canny边缘检测
class canny():
    #将RGB图像转化为灰度图像
    def gray(self,img_path):
        img=plt.imread(img_path)
        img_rgb=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
        img_gray=np.dot(img_rgb[...,:3],[0.299,0.587,0.114])
        return img_gray

    #高斯滤波平滑图像
    def smooth(self,img_gray,sigmal1=1.4,sigmal2=1.4):
        sigmal1=sigmal1
        sigmal2=sigmal2
        gau_sum=0
        gaussian=np.zeros([5,5])
        for i in range(5):
            for j in range(5):
                gaussian[i,j]=math.exp((-1/(2*sigmal2*sigmal1))*(np.square(i-3)+
                                                               np.square(j-3)))/(2*math.pi*sigmal1*sigmal2)
                gau_sum=gau_sum+gaussian[i,j]
            gaussian=gaussian/gau_sum
            W,H=img_gray.shape
            new_gray=np.zeros([W-5,H-5])
            for i in range(W-5):
                for j in range(H-5):
                    new_gray[i,j]=np.sum(img_gray[i:i+5,j:j+5]*gaussian)
        return new_gray
    #计算dx,dy,M,thana
    def gradients(self,new_gray):
        W,H=new_gray.shape
        dx=np.zeros([W-1,H-1])
        dy=np.ones([W-1,H-1])
        M=np.zeros([W-1,H-1])
        theta=np.zeros([W-1,H-1])
        for i in range(W-1):
            for j in range(H-1):
                dx[i,j]=new_gray[i+1,j]-new_gray[i,j]
                dy[i,j]=new_gray[i,j+1]-new_gray[i,j]
                M[i,j]=np.sqrt(np.square(dx[i,j])+np.square(dy[i,j]))
                theta[i,j]=math.atan(dx[i,j]/(dy[i,j]+0.0000001))
        return dx,dy,M,theta

    #非最大抑制方案1
    def NMS1(self,M,dx,dy,theta):
        #定义常数，将弧度转化为度
        gree=180.0/math.pi
        W,H=np.shape(M)
        #获取角度值
        d = np.copy(theta)
        NMS=np.zeros((W,H))
        NMS[0,:]=NMS[W-1,:]=NMS[:,0]=NMS[:,H-1]=0
        for i in range(1,W-1):
            for j in range(1,H-1):
                if M[i,j]!=0:
                    gradTemp=d[i][j]*gree
                    #水平边缘
                    if((-157.5<=gradTemp<=157.5) or (-22.5<=gradTemp<=22.5)):
                        if(M[i][j]>M[i-1][j] and M[i][j]>M[i+1][j]):
                            NMS[i][j]=M[i][j]
                    #45°边缘
                    if((112.5<=gradTemp<=157.5) or (-67.5<=gradTemp<=-22.5)):
                        if(M[i][j]>M[i+1][j-1] and(M[i][j]>M[i-1][j+1])):
                            NMS[i][j]=M[i][j]
                    #垂直边缘
                    if((-112.5<=gradTemp<=-67.5) or (67.5<=gradTemp<=122.5)):
                        if(M[i][j]>M[i-1][j]and(M[i][j]>M[i][j+1])):
                            NMS[i][j]=M[i][j]
                    #-45°边缘
                    if((-157.5<=gradTemp<=112.5) or (22.5<=gradTemp<=67.5)):
                        if(M[i][j]>M[i-1][j-1]and(M[i][j]>M[i+1][j+1])):
                            NMS[i][j]=M[i][j]
        return NMS

    #非最大抑制方案2
    def NMS(self,M,dx,dy):
        #M:梯度
        #dx:x方向导数
        #dy:y方向导数
        d=np.copy(M)
        W,H=M.shape
        NMS=np.zeros((W,H))
        NMS[0,:]=NMS[W-1,:]=NMS[:,0]=NMS[:,H-1]=0
        for i in range(1,W-1):
            for j in range(1,H-1):
                #找到可能边缘点
                if M[i,j]!=0:
                    #x方向导数
                    gradx=dx[i,j]
                    #y方向导数
                    grady=dy[i,j]
                    #当前梯度
                    gradTemp=M[i,j]
                    #如果 x 方向梯度值比较大，说明导数方向趋向于 x 分量
                    if np.abs(gradx)>np.abs(grady):
                        #权重
                        weight=np.abs(grady)/np.abs(gradx)
                        grad2=M[i-1,j]
                        grad4=M[i+1,j]
                        if gradx*grady>0:
                            # 如果 x, y 方向导数符号一致
                            # 像素点位置关系
                            # g1
                            # g2  c  g4
                            #        g3
                            grad1=M[i-1,j-1]
                            grad3=M[i+1,j+1]
                        else:
                            # 如果 x，y 方向导数符号相反
                            # 像素点位置关系
                            #        g3
                            # g2  c  g4
                            # g1
                            grad1=M[i-1,j+1]
                            grad3=M[i+1,j-1]
                    else:
                        weight=np.abs(gradx)/np.abs(grady)
                        grad2=M[i,j-1]
                        grad4=M[i,j+1]
                        # 如果 x, y 方向导数符号相反
                        # 像素点位置关系
                        #    g2 g1
                        #    c
                        # g3 g4
                        if gradx*grady<0:
                            grad1=M[i+1,j-1]
                            grad3=M[i-1,j+1]
                        # 如果 x，y 方向导数符号一致
                        # 像素点位置关系
                        # g1 g2
                        #    c
                        #    g4  g3
                        else:
                            grad1=M[i-1,j-1]
                            grad3=M[i+1,j+1]
                    #分别计算两个方向的灰度差值
                    gradTemp1=weight*grad2+(1-weight)*grad1
                    gradTemp2=weight*grad4+(1-weight)*grad3
                    #若该梯度均大于差值的灰度值，则保留，否则赋值为零，抑制
                    if gradTemp>=gradTemp1 and gradTemp>=gradTemp2:
                        NMS[i,j]=gradTemp
        return NMS

    #双阈值处理
    def double_threshold(self,NMS):
        W,H=NMS.shape
        DT=np.zeros([W,H])
        #高低阈值比为：1：3
        TL=0.1*np.max(NMS)
        TH=0.3*np.max(NMS)

        for i in range(1,W-1):
            for j in range(1,H-1):
                #将低于最小阈值都设为0
                if(NMS[i,j]<TL):
                    DT[i,j]=0
                #将大于最高阈值都设为1
                elif(NMS[i,j]>=TH):
                    DT[i,j]=255

                #用8连通方法得到高低阈值间的边缘像素
                elif((NMS[i-1,:]>=TH).any()) or ((NMS[i+1,:]>=TH).any()) or ((NMS[i,[j-1,j+1]]>=TH).any()):
                    DT[i,j]=255
                # elif((NMS[i-1,[j-1,j+1]>TH].any())or((NMS[i+1,[j-1,j+1]]>TH).any())or((NMS[i,[j-1,j+1]]>TH).any())):
                #     DT[i,j]=255
        return DT