201971010245-王亚亚 实验二 个人项目—《D{0-1}背包问题》项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | https://edu.cnblogs.com/campus/xbsf/2019nwnucs |
| 这个作业要求链接 | https://edu.cnblogs.com/campus/xbsf/2019nwnucs/homework/12527 |
| 我的课程学习目标 | 1. 掌握软件项目个人开发流程。 2. 掌握Github发布软件项目的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | 1. 熟悉了软件项目源代码常用集成开发软件工具。 2.了解了Github发布软件项目的操作方法 3.了解个各种代码管理软件的特点与区别。 |
| 项目Github的仓库链接地址 | https://github.com/201971010245/245D0-1 |
实验内容
任务1:阅读教师博客“常用源代码管理工具与开发工具
完成任务1后,对三位同学进行了点评实验点评如下:
| 项目 | 内容 |
|---|---|
| 梁春云同学作业评价链接 | https://www.cnblogs.com/liangchunyun/p/15969570.html |
| 谢雨涵同学作业评价链接 | https://www.cnblogs.com/201971010247xyh/p/15966838.html |
| 孙得弘同学作业评价链接 | https://www.cnblogs.com/sundh1017/p/15954270.html |
任务2:总结详细阅读《构建之法》第1章、第2章,掌握PSP流程
阅读《构建之法》第1章,第2章,第3章总结链接如下:
- 第一章
- 软件构建的过程
构建不仅仅是cc和link命令,以后复杂的软件不但要有合理的软件构架、软件设计与实现,还要有各种文件和数据来描述各个程序文件之间的依赖关系、编译参数、链接参数,等等。
2.软件=程序+软件工程
3.软件企业=软件+商业模式
4.软件的特殊性
- 复杂性
- 不可见性
- 易变性
- 服从性
- 非连续性
- PSP流程如下:
| p | 预估时间 (min) | 实际完成时间(min) |
|---|---|---|
| 计划 | 8 | 9 |
| 开发 | 85 | 90 |
| 需求分析 | 8 | 10 |
| 生成设计文档 | 2 | 5 |
| 设计复审 | 4 | 5 |
| 代码规划 | 2 | 2 |
| 具体设计 | 5 | 5 |
| 具体编码 | 30 | 35 |
| 代码复审 | 10 | 8 |
| 测试 | 4 | 3 |
| 测试报告 | 5 | 5 |
| 计算工作量 | 5 | 5 |
| 事后总结,并提出过程改进计划 | 10 | 10 |
任务3:项目开发
- 任务描述如下:
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
{0-1}KP数据集是研究{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解{0-1}背包问题的经典算法。查阅相关资料,设计一个采用贪心算法、动态规划算法、回溯算法求解{0-1}背包问题的程序 - 需求分析
- 数据集文件进行数据读取;
- 对某一组数据进行可视化,以散点图的方式呈现给用户;
- 将数据按照一定顺序进行排序;
- 通过回溯算法和动态规划算法进行程序实现,将结果存入文件
- 功能设计
1.可正确读入实验数据文件的有效{0-1}KP数据;
2.能够绘制任意一组{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
3.能够对一组{0-1}KP数据按重量比进行非递增排序;
4.用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位);
5.任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。 - 任务分析:
01背包属于找最优解问题,用回溯法需要构造解的子集树。对于每一个物品i,对于该物品只有选与不选2个决策,总共有n个物品,可以顺序依次考虑每个物品,这样就形成了一棵解空间树: 基本思想就是遍历这棵树,以枚举所有情况,最后进行判断,如果重量不超过背包容量,且价值最大的话,该方案就是最后的答案。
在搜索状态空间树时,只要左子节点是可一个可行结点,搜索就进入其左子树。对于右子树时,先计算上界函数,以判断是否将其减去(剪枝)。 - 设计实现
- 利用动态规划算法和回溯算法来实现{0-1}背包问题,可以用一个二维数组来记录背包的状态。假设用value[N][V]来存储中间状态值,value[i][j]表示前i件物品能装入容量为j的背包中的物品价值总和的最大值,则我们最终只需求知value[i=N][j=V]的值。
1) 若w[i]>j,则第i件物品肯定不能装入容量为j的背包,此时value[i][j]=value[i-1][j]
- 若w[i]<=j,则首先明确的是这件物品是可以装入容量为j的背包的,那么如果我们将该物品装入,则有
value[i][j]=value[i-1][j-w[i]]+v[i]
2.流程图
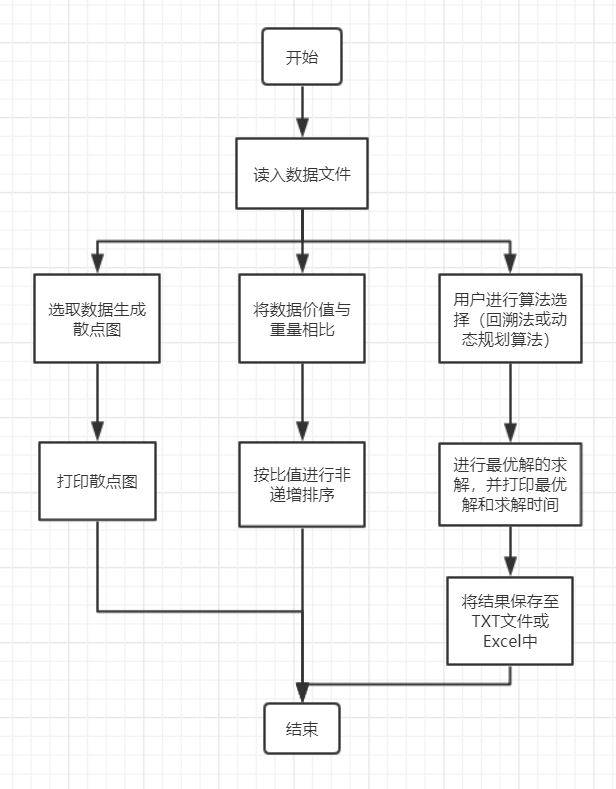
-
测试运行
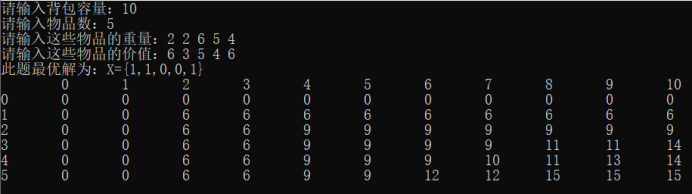
-
代码片段
- 散点图
点击查看代码
x = np.linspace(0.05, 10, 1000)
np.random.seed(22)
y = np.random.randn(1000)
# 图表元素中正常显示中文字符
plt.rcParams['font.sans-serif'] = 'SimHei'
# 坐标轴刻度标签正常显示负号
plt.rcParams['axes.unicode_minus'] = False
plt.scatter(x, y,
s=87, # 标记点大小
marker='*', # 标记点的样式 星号
c='g', # green 绿色
linewidths=0.41,
edgecolor='y', # 边缘颜色
label='scatter figure')
plt.xticks(size=12, color='grey') # x 轴刻度标签
plt.yticks(size=12, color='grey') # y 轴刻度标签
plt.title('散点图', size=14, color='y'); # 添加图表标题
plt.legend() # 添加图例
# 设置坐标轴刻度范围
plt.xlim(-0.5, 10.5)
plt.ylim(-3.5, 3.5);
2.主程序代码块
点击查看代码
if __name__ == '__main__':
fileName = getData()
# 列表中包含若干个子列表,每个子列表包含一组数据的价值信息,每个子列表又包含若干个三元组列表,三元组列表记录了记录了该组数据每个项集
print('数据读入完成!')
print('价值信息:')
for i in profit[0]:
print(i)
# 同价值信息,用于记录重量信息
print('重量信息:')
print(weight)
# 列表包含若干子列表,一个子列表表示一组数据的价值-重量-价值重量比信息,子列表分为若干九元组。九元组记录了改组数据的价值-重量-价值重量比九条信息
print('价值-重量-价值重量比信息:')
print(prowei)
while (True):
x = int(input('请选择:\n1、画散点图\n2、非递增排序\n3、求解\n'))
if x == 1:
n = int(input('请选择对第几条数据做散点图'))
show(n - 1)
continue
elif x == 2:
n = int(input('请选择要对第几条数据进行排序'))
sort(n - 1)
continue
elif x == 3:
n = int(input('请选择算法\n1、回溯法\n2、动态规划算法\n'))
num = int(input('请输入要求解第几组数据'))
maxWeight = int(input('请输入背包容纳的最大重量'))
if n == 1:
profit[num - 1] = [[0, 0, 0]] + profit[num - 1]
weight[num - 1] = [[0, 0, 0]] + weight[num - 1]
for i in profit[0]:
print(i)
time1 = time.time()
huisu(num - 1, maxWeight, 0, 0, 0, 0)
time2 = time.time()
endMax.sort(reverse=True)
print('最大价值:' + str(endMax[0]))
print('运行时间:' + str(time2 - time1) + 's')
for item in range(len(pathList)):
if pathList[item] == endMax[0]:
path(item, num - 1)
elif n == 2:
time1 = time.time()
dp(num - 1, maxWeight)
time2 = time.time()
print(time2 - time1)
x = int(input('请选择:\n1.保存为txt\n2.不保存'))
if x == 1:
saveTxt(fileName, num, maxWeight, endMax[0], time2 - time1)
else:
pass
else:
print('输入有误,请重新输入!')
continue
- 项目总结
此次实验主要是关于背包问题的动态规划法、回溯法求解背包问题,在程序设计过程中,按程序功能进行分块,通过模块化的设计,让我更加理解了软件功能需求,同时也提高了我程序完成的效率。




