一、概述
1.基本工作原理:存在一个带有标签的样本集,即我们知道样本中的每个数据与所属分类的对应关系。输入没有标签的数据,将新数据的每个特征与样本中数据的对应特征进行比较,算法提取最相似样本的分来标签。选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
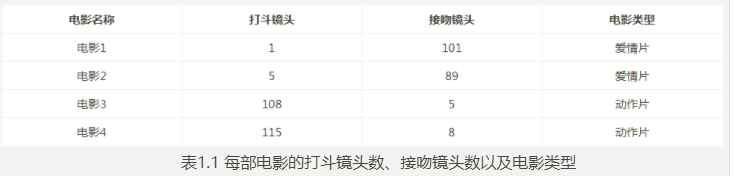
例如上表训练样本集。这个数据集有两个特征,即打斗镜头数和接吻镜头数。分类标签为爱情片和动作片。大致可以观察发现接吻镜头多的是爱情片,打斗镜头多的是动作片。而k-近邻算法可以做到,你告诉它这个电影打斗镜头数为2,接吻镜头数为102,它会依据数据经验告诉你这个是爱情片。但是依据样本数据集k-近邻算法的眼里,电影类型只有爱情片和动作片,它会提取样本集中特征最相似数据(最邻近)的分类标签,得到的结果可能是爱情片,也可能是动作片,但绝不会是"爱情动作片"。当然,这些取决于数据集的大小以及最近邻的判断标准等因素。
2.距离计算

我们可以从散点图大致推断,这个红色圆点标记的电影可能属于动作片,因为距离已知的那两个动作片的圆点更近。k-近邻算法用什么方法进行判断呢?没错,就是距离度量。这个电影分类的例子有2个特征,也就是在2维实数向量空间,可以使用我们高中学过的两点距离公式计算距离,即
通过计算,我们可以得到如下结果:
- 新数据(101,20)距离动作片(108,5)的距离约为16.55
- 新数据(101,20)距离动作片(115,8)的距离约为18.44
- 新数据(101,20)距离爱情片(5,89)的距离约为118.22
- 新数据(101,20)距离爱情片(1,101)的距离约为128.69
通过计算可知,红色圆点标记的电影到动作片 (108,5)的距离最近,为16.55。如果算法直接根据这个结果,判断该红色圆点标记的电影为动作片,这个算法就是最近邻算法,而非k-近邻算法。
k-近邻算法步骤如下:
- 计算已知类别数据集中的点与当前点之间的距离;
- 按照距离递增次序排序;
- 选取与当前点距离最小的k个点;
- 确定前k个点所在类别的出现频率;
- 返回前k个点所出现频率最高的类别作为当前点的预测分类。
比如,现在我这个k值取3,那么在电影例子中,按距离依次排序的三个点分别是动作片(108,5)、动作片(115,8)、爱情片(5,89)。在这三个点中,动作片出现的频率为三分之二,爱情片出现的频率为三分之一,所以该红色圆点标记的电影为动作片。这个判别过程就是k-近邻算法。
但是,电影例子中的特征是2维的,这样的距离度量可以用两点距离公式计算,但是如果是更高维的呢?我们可以用欧氏距离(也称欧几里德度量),我们高中所学的两点距离公式就是欧氏距离在二维空间上的公式,也就是欧氏距离的n的值为2的情况。
应该还有其他计算距离的方法,待补充.....切比雪夫距离、马氏距离 巴氏距离等
二、算法
k-近邻算法
三、使用
上面学习了简单的k-近邻算法的实现方法,但是这并不是完整的k-近邻算法流程,k-近邻算法的一般流程:
1.收集数据:可以使用爬虫进行数据的收集,也可以使用第三方提供的免费或收费的数据。一般来讲,数据放在txt文本文件中,按照一定的格式进行存储,便于解析及处理。
2.准备数据:使用Python解析、预处理数据。
3.分析数据:可以使用很多方法对数据进行分析,例如使用Matplotlib将数据可视化。
4.测试算法:计算错误率。
5.使用算法:错误率在可接受范围内,就可以运行k-近邻算法进行分类。
6.代码实现:待补充
四、参数
KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)
KNneighborsClassifier参数说明:
- n_neighbors:默认为5,就是k-NN的k的值,选取最近的k个点。
- weights:默认是uniform,参数可以是uniform、distance,也可以是用户自己定义的函数。uniform是均等的权重,就说所有的邻近点的权重都是相等的。distance是不均等的权重,距离近的点比距离远的点的影响大。用户自定义的函数,接收距离的数组,返回一组维数相同的权重。
- algorithm:快速k近邻搜索算法,默认参数为auto,可以理解为算法自己决定合适的搜索算法。除此之外,用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索,brute是蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时。kd_tree,构造kd树存储数据以便对其进行快速检索的树形数据结构,kd树也就是数据结构中的二叉树,关于algorithm参数kd_tree的原理,可以查看《统计学方法 李航》书中的讲解。以中值切分构造的树,每个结点是一个超矩形,在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的,其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体。
- leaf_size:默认是30,这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度,同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
- metric:用于距离度量,默认度量是minkowski,也就是p=2的欧氏距离(欧几里德度量)。
- p:距离度量公式。在上小结,我们使用欧氏距离公式进行距离度量。除此之外,还有其他的度量方法,例如曼哈顿距离。这个参数默认为2,也就是默认使用欧式距离公式进行距离度量。也可以设置为1,使用曼哈顿距离公式进行距离度量。
- metric_params:距离公式的其他关键参数,这个可以不管,使用默认的None即可。
- n_jobs:并行处理设置。默认为1,临近点搜索并行工作数。如果为-1,那么CPU的所有cores都用于并行工作。
五、特别之处
优点
- 简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;
- 可用于数值型数据和离散型数据;
- 训练时间复杂度为O(n);无数据输入假定;
- 对异常值不敏感
缺点
- 计算复杂性高;空间复杂性高;
- 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
- 一般数值很大的时候不用这个,计算量太大。但是单个样本又不能太少,否则容易发生误分。
- 最大的缺点是无法给出数据的内在含义。
参考资料:
1.机器学习实战教程(一):K-近邻算法(史诗级干货长文) | Jack Cui
2.《机器学习实战》。
3.《统计学习方法 李航》。



