图论二：图的存储

一、邻接矩阵：就是一个二维数组

特点：对称（矩阵有对称性），空间代价大（空间需求为O(|v|^2)），适用于稠密图，否则空间浪费较大。

 

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = 120;
const int INF = 0x3fff;
int a[maxn][maxn],n;
void Init()
{
    int i,j;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
        a[i][j]=INF;
}
void Print()
{
    int i,j;
    for(i=1;i<=n;i++)
    {
        cout<<i<<"的邻接点有："; 
        for(j=1;j<=n;j++)
            if(a[i][j]!=INF) cout<<"a["<<i<<"]["<<j<<"]="<<a[i][j]<<" ";
        cout<<endl;
    }
}
int main(void)
{
    int i,j,x,m,y,z;
    cin>>n>>m;
    Init();
    for(i=0;i<m;i++)
    {
        cin>>x>>y>>z;
        a[x][y]=a[y][x]=z;
    }
    Print();
    return 0;
}
/*
测试数据：
5 4
1 2 1
2 3 4
4 5 7 
4 3 9
*/

 

二、邻接矩阵：散列表或者多重表

特点：适用于稀疏矩阵，存储空间较小为O(2*|E|)。

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

struct Node{
    int data,dis;
    struct Node *next;
};

struct LNode{
    struct Node *First;
    struct LNode *NEXT;
};

typedef struct LNode *Lin;
int vis[120],m,n;

Lin Find(int x,Lin T)
{
    Lin p=T;
    while(p!=NULL)
    {
        if(p->First->data==x) break;
        p=p->NEXT;
    }
    return p;
}

void Insert(int x,int dis,struct Node* T)
{
    struct Node* tp=T;
    while(tp->next!=NULL) tp=tp->next;
    struct Node* p=(struct Node*)malloc(sizeof(struct Node));
    p->data=x;
    p->dis=dis;
    p->next=tp->next;
    tp->next=p;
    //return T;
}

void dfs(Lin T,int fa,int dis)
{
    if(T==NULL) return ;
    if(fa) printf("深搜遍历图的一条边：(%d->%d)，边的长度为： %d\n",fa,T->First->data,dis);
    fa=T->First->data;
    for(struct Node* p=T->First->next;p!=NULL;p=p->next)
    {
        Lin tp=Find(p->data,T);
        if(vis[p->data]==0)
        {
            vis[p->data]=1;
            dfs(tp,fa,p->dis);
            vis[p->data]=0;
        }
    }
}

int main(void)
{
    int i,j,x,y,dis;
    Lin T,p,tp;
    T=(Lin)malloc(sizeof(struct LNode));
    T->NEXT=NULL;
    p=T;
    printf("请输入图的顶点数和边数：\n");
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
    {
        tp=(Lin)malloc(sizeof(struct LNode));
        tp->First=(struct Node*)malloc(sizeof(struct Node));
        tp->First->data=i;
        tp->First->next=NULL;
        tp->NEXT=p->NEXT;
        p->NEXT=tp;
        p=p->NEXT;
    }
    
    printf("请输入图的边：\n");
    for(i=0;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&dis);
        p=Find(x,T);
        Insert(y,dis,p->First);
        p=Find(y,T);
        Insert(x,dis,p->First);
    }
    memset(vis,0,sizeof(vis));
    dfs(T->NEXT,0,0);
    return 0;
}

/*
测试样例： 
5 5
1 2 34
2 3 45
3 4 13
1 4 66
5 1 29
*/

 

三、十字链表（适用于有向图）

 1、定义：是一种链式存储结构，可以视为邻接表和逆邻接表的结合，既可以求入度，也可以求出度，十分方便。

 解释：

（1）普通的邻接表可以求出入度，普通的逆邻接表可以求出出度，而十字链表可以求出入度+出度。

（2）十字链表对于有向图来说还是非常方便的既可以正向遍历节点，也可以反向进行，类似于双向链表。

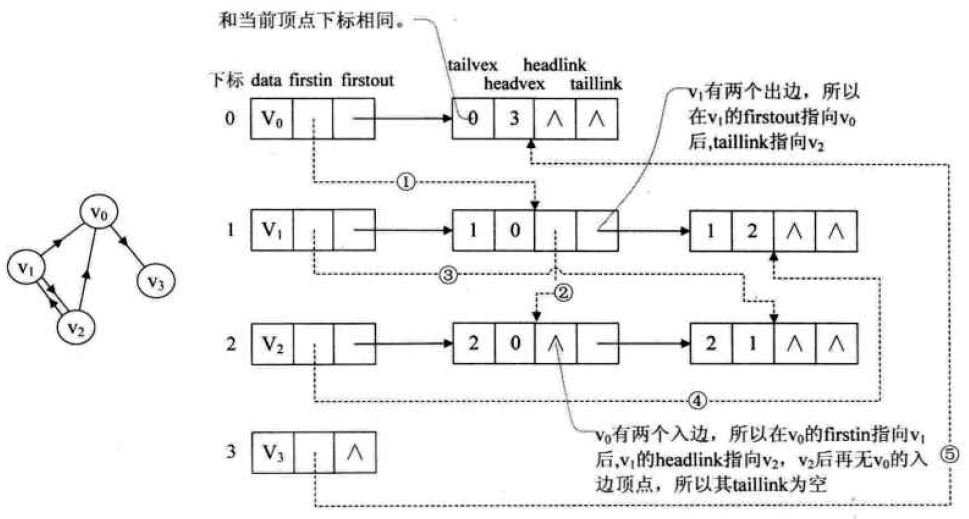
2、存储结构：

（1）边节点：每个边界点存储4个变量：tailvex（一条边起点的ID），headvex（一条边终点的ID），taillink（一条边入边的指针），

headlink（一条边出边的指针）。（还可以有存储边的权值的数据）。

（2）点节点：有两个指针：First_IN（表示第一个入度的节点），First_Out（表示第一个出度的节点），data（表示这个节点的编号）。

每个顶点的信息，作为边之间传值的中转站，可以从一条边跑到另一条边。

（3）图结构：VertexNum（点的数量），EdgeNum（边的数量），cur数组（记录图中每个节点的信息）。

 

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
const int maxn = 1200;

struct EdgeNode{ //边结构体 
    int tailvex,headvex;
    struct EdgeNode *taillink,*headlink;
};
typedef struct EdgeNode* Edge;

struct VertexNode{ //点结构体 
    int data;
    Edge First_IN,First_OUT;
}; 
typedef struct VertexNode* Vertex;

struct GraphNode{ //图的总结构 
    int VertexNum,EdgeNum; 
    struct VertexNode cur[maxn];
};
typedef struct GraphNode* Graph;

void Create_Graph(Graph &G) //构造一个图 
{
    int i,x,y,z;
    G=(Graph)malloc(sizeof(struct GraphNode));
    scanf("%d%d",&G->VertexNum,&G->EdgeNum);
    for(i=1;i<=G->VertexNum;i++)
    {
        G->cur[i].data=i;
        G->cur[i].First_IN=NULL;
        G->cur[i].First_OUT=NULL;
    }
    
    for(i=1;i<=G->EdgeNum;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        Edge e=(Edge)malloc(sizeof(struct EdgeNode));
        e->tailvex=x;  //out是出度 ，构建邻接表 
        e->taillink=G->cur[x].First_OUT;
        G->cur[x].First_OUT=e;
        
        e->headvex=y; //in是入度，构建逆邻接表 
        e->headlink=G->cur[y].First_IN;
        G->cur[y].First_IN=e; 
    }
}

void Show(Graph G) //展示图的入度和出度。 
{
    int i,num;
    Edge e;
    for(i=1;i<=G->VertexNum;i++)
    {
        printf("%d节点的:",G->cur[i].data);
        num=0;
        e=G->cur[i].First_IN;
        while(e!=NULL)
        {
            num++;
            e=e->headlink;
        }
        printf("入度是：%d\t",num);
        
        num=0;
        e=G->cur[i].First_OUT;
        while(e!=NULL)
        {
            num++;
            e=e->taillink;
        }
        printf("出度是：%d\n",num); 
    }
}

int main(void)
{
    Graph G;
    Create_Graph(G);
    Show(G);
    return 0;
}

/*
测试数据： 
5 4
1 2 3
2 3 2
3 4 1
4 5 5
*/

 

四、邻接多重表

参考文章：http://www.cnblogs.com/Trojan00/p/8964609.html

 思路：邻接多重表主要用于存储无向图，每条边的边界点分别在以该边所依附的两个顶点为头结点的链表中，对于已经找到过的边要做标记。

 

 

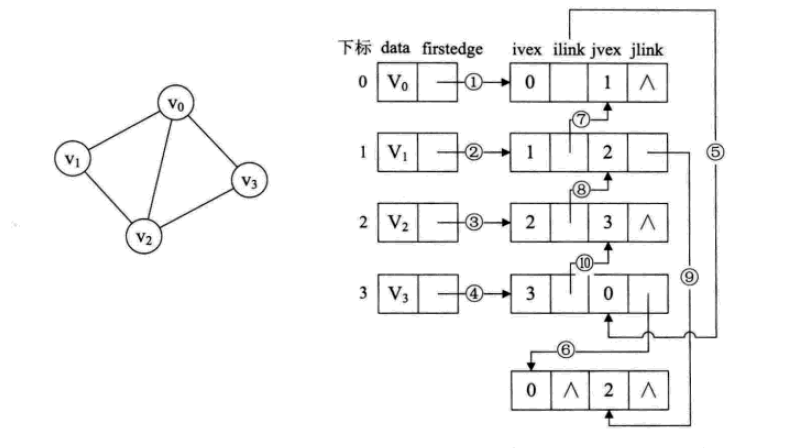
代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
const int maxn = 1200;
int vis[maxn]={0};
struct EdgeNode{ //图的边结构 
    int weight,mark;
    int ivec,jvex;
    struct EdgeNode *ilink,*jlink; 
};
typedef struct EdgeNode* Edge;

struct VertexNode{ //图的点结构 
    int id;
    Edge Firstarc;
};
typedef struct VertexNode* Vertex;

struct GraphNode{ //图的结构 
    VertexNode cur[maxn];
    int VertexNum,EdgeNum;
};
typedef struct GraphNode *Graph;

int Locate(Graph G,int pos)
{
    for(int i=1;i<=G->VertexNum;i++)
    if(G->cur[i].id==pos) return i;
    return -1;
}
 
Graph Create()
{
    int i,x,y,z;
    Graph G=(Graph)malloc(sizeof(struct GraphNode));
    cout<<"请输入图的节点数目和边的数目："<<endl; 
    cin>>G->VertexNum>>G->EdgeNum;
    
    for(i=1;i<=G->VertexNum;i++) //初始化图的每一个节点 
    {
        G->cur[i].id=i;
        //G->cur[i].Firstarc=(Edge)malloc(sizeof(struct EdgeNode));
        G->cur[i].Firstarc=NULL;
    }
    
    for(i=1;i<=G->EdgeNum;i++)
    {
        cin>>x>>y>>z;
        int t1=Locate(G,x);
        int t2=Locate(G,y);
        if(t1<0||t2<0) printf("ERROR\n");
        Edge tp=(Edge)malloc(sizeof(struct EdgeNode));
        tp->ivec=t1;
        tp->jvex=t2;
        tp->weight=z;
        
        tp->mark=0;
        tp->ilink=G->cur[t1].Firstarc;
        tp->jlink=G->cur[t2].Firstarc;
        G->cur[t1].Firstarc=tp;
        G->cur[t2].Firstarc=tp;
    }
    return G;
}

void Dfs(Graph G,int x)
{
    cout<<G->cur[x].id<<" ";
    Edge p=G->cur[x].Firstarc;
    vis[x]=1;
    while(p!=NULL)
    {
        int i=(p->ivec==x?p->jvex:p->ivec);
        if(!vis[i]) Dfs(G,i);
        p=(p->ivec==x?p->jlink:p->ilink);
    }
}

int main(void)
{
    Graph G=Create();
    Dfs(G,1);
    return 0;
}

/*
4 5
1 2 1
2 3 1
3 4 2
2 4 3
1 4 2

*/