各种模拟
此帖功利心过强,弃更
全站最高浏览量,全是本人反省时刷的
2019/7/16

rank 20/51
嗯嗯,确实比较接近noip的难度了,第一次体验到自己想到正解的快感。然而成绩不尽人意.
T1:概率DP,显然,犯难,日常不会概率DP。(题目讲的辣莫短,我系不系理解错了?猜题意,昂,能同时取两件吗?不忘看一眼数据范围,N<=20,状压好像只能开到15,emmm,果断放弃状压[其实能开到20].)哈哈,把T2搞定,T3打完后,我又回来了,我是来拿那10%的,打个处理N==1的暴搜,心里美滋滋。
结果下来,脸都黑了,期望暴搜,精度不会卡,而且N==1,输出(1/P[1])就可以啦???!!!!

1 #include<cstdio>
2 #include<iostream>
3 #define MAXN 25
4 #define reg register int
5 using namespace std;
6 int N;
7 int W[MAXN];
8 double P[MAXN];
9 double ans;
10 void dfs(int pos,int gl){
11 double lin=(pos+1)*P[1]*gl;
12 ans+=lin;
13 lin=(pos+1)*(1-P[1])*gl;
14 if(lin>=0.0001){
15 dfs(pos+1,gl*(1-P[1]));
16 }
17 }
18 int sum;
19 int main(){
20 scanf("%d",&N);
21 for(reg i=1;i<=N;++i){
22 scanf("%lf%d",&P[i],&W[i]);
23 sum+=W[i];
24 }
25 if(N==1){
26 printf("%d\n",W[1]);
27 dfs(0,1);
28 printf("%.3lf\n",ans);
29 return 0;
30 }
31 printf("%d\n",sum);
32 if(N==3){
33 puts("12.167");
34 return 0;
35 }
36 puts("24.123");
37 return 0;
38 }
39 /*
40 N=1 emmm...
41 */
T2:昂?出题人玩b站?追番? 问路径最小费用,!!!!!,终于考图论了,我板子码的不赖(老泪纵横)。相互之间无费用,显然缩点,sb题,问整体,索完点跑克鲁斯卡尔就行了(信誓旦旦)。30min后,输样例,秒过,kx得一批。先看第三题,对拍先不打了。10min后,不对劲,第一次考水题,我要是没A岂不是很没面子,而且排名也高不了。恩,自信的码了10分的特判,昂,还要清零,检查数据范围。沉思ing,Kru不对,这是有向图,完呐,完呐,用topu保证考虑到最小权值,搞贪心。先啐一口,然后码topu,幸好老子机智,我都考虑这么多,一定能A掉。QAQ,90?,特判没清零,我真想锤死自己。

1 #include<queue>
2 #include<cstdio>
3 #include<cstring>
4 #include<iostream>
5 #include<vector>
6 #include<algorithm>
7 #define MD 50010
8 #define ME 100010
9 #define ll long long
10 #define reg register int
11 using namespace std;
12 inline int minn(int a,int b){
13 return a<b?a:b;
14 }
15 inline int read(){
16 int s=0;
17 char ch=getchar();
18 while(ch<'0'||ch>'9')ch=getchar();
19 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
20 return s;
21 }
22 ll ans;
23 struct rr{
24 int inext,to;
25 int w;
26 }bl[ME],tbl[ME];
27 int thead[MD],ttot,head[MD],itot;
28 void add(int x,int y,int z){
29 bl[++itot].w=z;
30 bl[itot].to=y;
31 bl[itot].inext=head[x];
32 head[x]=itot;
33 }
34 void tadd(int x,int y,int z){
35 tbl[++ttot].w=z;
36 tbl[ttot].to=y;
37 tbl[ttot].inext=thead[x];
38 thead[x]=ttot;
39 }
40 int N,M;
41 int root=1;
42 int dfn[MD],low[MD],num;
43 int stack[MD],top;
44 bool instack[MD];
45 int tot,belong[MD];
46 void tarjan(int u){
47 low[u]=dfn[u]=++num;
48 stack[++top]=u;//
49 instack[u]=true;
50 int tto;
51 for(reg i=head[u];i;i=bl[i].inext){
52 if(!dfn[tto=bl[i].to]){
53 tarjan(tto);
54 low[u]=minn(low[u],low[tto]);
55 }
56 else if(instack[tto])
57 low[u]=minn(low[u],dfn[tto]);
58 }
59 if(dfn[u]==low[u]){
60 int tan=stack[top];
61 ++tot;
62 while(tan!=u){
63 belong[tan]=tot;
64 instack[tan]=false;
65 tan=stack[--top];
66 }
67 --top;
68 belong[u]=tot;
69 instack[u]=false;
70 }
71 }
72 int ru[MD];
73 void init(){
74 int x,y;
75 for(int i=1;i<=N;++i){
76 x=belong[i];
77 // printf("orz belong[%d]=%d\n",i,x);
78 for(reg j=head[i];j;j=bl[j].inext){
79 y=belong[bl[j].to];
80 if(x==y)continue;
81 tadd(x,y,bl[j].w);
82 ++ru[y];
83 }
84 }
85 }
86 queue<int >dd;
87 int zui[MD];
88 void topu(){
89 int tto;
90 dd.push(belong[root]);
91 zui[belong[root]]=0;
92 while(!dd.empty()){
93 int ltop=dd.front();dd.pop();
94 for(reg i=thead[ltop];i;i=tbl[i].inext){
95 tto=tbl[i].to;
96 --ru[tto];
97 zui[tto]=minn(zui[tto],tbl[i].w);
98 if(!ru[tto])
99 dd.push(tto);
100 }
101 }
102 }
103 void shan(){
104 ttot=tot=num=itot=0;
105 ans=0;
106 memset(thead,0,sizeof(thead));
107 memset(head,0,sizeof(head));
108 // memset(belong,0,sizeof(belong));
109 // memset(ru,0,sizeof(ru));
110 memset(zui,0x7f,sizeof(zui));
111 memset(low,0,sizeof(low));
112 memset(dfn,0,sizeof(dfn));
113 }
114 int main(){
115 // freopen("da.in","r",stdin);///!!!!!!
116 while(1){
117 // printf("orz tiao _____________\n");
118 N=read();M=read();
119 if(N+M==0)break;
120 int xi,yi,ci;
121 if(M==N-1){
122 for(reg i=1;i<=M;++i){
123 read();read();ci=read();
124 ans+=1ll*ci;
125 }
126 printf("%lld\n",ans);
127 continue;
128 }
129 shan();
130 for(reg i=1;i<=M;++i){
131 xi=read()+1;yi=read()+1;ci=read();
132 add(xi,yi,ci);
133 }
134 tarjan(1);
135 init();
136 topu();
137 for(reg i=1;i<=tot;++i)
138 ans+=1ll*zui[i];
139 printf("%lld\n",ans);
140 }
141 return 0;
142 }
143 /*
144 clear
145 10% 树,无环,ans=sum(edge)
146 tarjan+Kru kru=wrong
147 topu=defen
148 */
T3:第一眼,区间DP,搞一下,woc,N到50000,失败,还是搞暴力吧,N<=5000,区间和,N>5000,lower_bound(),贼爽。在扫一眼题目,每行每列只有一只军队,状压?,5000也开不了啊。emmm...莫不是bitset(学长昨天刚讲)。无限yy中。看到wd等大神搞了64,zkt也优化成了55,emmm...,我优化都不会打,QAQ。正解是处理成序列问题,妙啊。

1 #include<cstdio>
2 #include<iostream>
3 #include<vector>
4 #include<algorithm>
5 #define MAXN 50010
6 #define reg register int
7 using namespace std;
8 inline int read(){
9 int s=0;
10 char ch=getchar();
11 while(ch<'0'||ch>'9')ch=getchar();
12 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
13 return s;
14 }
15 int N;
16 vector<int >hh[MAXN];
17 int heng[MAXN],zong[MAXN];
18 int ans;
19 int qsum[5010][5010];
20 bool cmp(int a,int b){
21 return a<b;
22 }
23 void tong(int h,int z,int len){
24 if(h+len-1>N)return ;
25 if(z+len-1>N)return ;
26 int zuo=z,you=z+len-1;
27 int l1,l2;
28 int sum=0;
29 for(reg i=h;i<=h+len-1;++i){
30 l1=lower_bound(hh[i].begin(),hh[i].end(),zuo)-hh[i].begin();
31 l2=upper_bound(hh[i].begin(),hh[i].end(),you)-hh[i].begin();
32 sum+=l2-l1;
33 }
34 if(sum==len)
35 ++ans;
36 }
37 void tong1(int h,int z,int len){
38 if(h+len-1>N)return ;
39 if(z+len-1>N)return ;
40 int zuo=z,you=z+len-1;
41 int sum=0;
42 for(reg i=h;i<=h+len-1;++i){
43 sum+=qsum[i][you]-qsum[i][zuo-1];
44 }
45 if(sum==len)
46 ++ans;
47 }
48 int main(){
49 // freopen("da.in","r",stdin);
50 ans=N=read();
51 ++ans;
52 for(reg i=1;i<=N;++i){
53 heng[i]=read();zong[i]=read();
54 hh[heng[i]].push_back(zong[i]);
55 }
56 if(N<=5000){
57 for(reg i=1;i<=N;++i)
58 if(!hh[i].empty()){
59 sort(hh[i].begin(),hh[i].end(),cmp);
60 for(reg k=0;k<hh[i].size();++k){
61 qsum[i][hh[i][k]]=1;
62 }
63 for(reg k=1;k<=N;++k)
64 qsum[i][k]=qsum[i][k]+qsum[i][k-1];
65 }
66 for(reg len=2;len<N;++len)
67 for(reg i=1;i<=N-len+1;++i)
68 for(reg j=1;j<=N-len+1;++j)
69 tong1(i,j,len);
70 printf("%d\n",ans);
71 return 0;
72 }
73 for(reg i=1;i<=N;++i)
74 if(!hh[i].empty())
75 sort(hh[i].begin(),hh[i].end(),cmp);
76 for(reg len=2;len<N;++len)
77 for(reg i=1;i<=N-len+1;++i)
78 for(reg j=1;j<=N-len+1;++j)
79 tong(i,j,len);
80 printf("%d\n",ans);
81 return 0;
82 }
83 /*
84 er chazhao+baoli
85 qian zhui he youhua
86 */
该骗到的分没骗到,优化意识不强。不够认真。
2019/7/18

rank 38/55
T1:先扫了所有题,T1和T3有些莫名的相似,估计和组合数有关系,(emmm还真和组合数有关系)。然而其实没任何思路,暴搜也不太会码,直接跳过。考场下来,得知是欧拉路时,挺懊悔自己概念不清,无意识。但当我现在过掉时,短短40行代码,就在朦胧的睡眼中A掉了。交流发现自己对于这种题方法完全免疫,(其实就是找规律)。姑且不说,学dfs序版lca时自己嗑了一顿欧拉序,whs大神画了几张图就粗来了???但是他带我水过太鼓达人 时(01序列找规律),我并没有认真思考这种题的心路历程,这是平时做的不到位...

1 #include<cstdio>
2 #include<iostream>
3 #define MAXN 100010
4 #define ll long long
5 using namespace std;
6 inline int read(){
7 int s=0;
8 char ch=getchar();
9 while(ch<'0'||ch>'9')ch=getchar();
10 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
11 return s;
12 }
13 struct rr{
14 int inext,to;
15 }bl[MAXN<<1];int head[MAXN],itot;
16 void add(int x,int y){
17 bl[++itot].to=y;
18 bl[itot].inext=head[x];
19 head[x]=itot;
20 }
21 int n,m;
22 ll ans;
23 short bian[MAXN<<1];
24 int lim;
25 void dfs(int u,int js){
26 // printf("u=%d js=%d\n",u,js);
27 bool ok=0;
28 for(int i=head[u];i;i=bl[i].inext){
29 if(bian[i]==2)continue;
30 if(!bian[i]){
31 ++bian[i];++bian[i^1];
32 ok=1;
33 dfs(bl[i].to,js);
34 --bian[i];--bian[i^1];
35 }
36 else{
37 if(js<lim){
38 ++bian[i];++bian[i^1];
39 ok=1;
40 dfs(bl[i].to,js+1);
41 --bian[i];--bian[i^1];
42 }
43 }
44 }
45 if(!ok)++ans;
46 return ;
47 }
48 int main(){
49 // freopen("da1.in","r",stdin);
50 itot=1;
51 n=read();m=read();
52 lim=m-2;
53 for(int i=1,a,b;i<=m;++i){
54 a=read();b=read();
55 add(a,b);add(b,a);
56 }
57 dfs(1,0);
58 printf("%lld\n",ans/(n-1));
59 }
60 /*
61 20% zhuang ya?
62 hai shi baosou ba ,
63 sha dou bu hui ma
64 */
以后做图论题,先手模数据找性质.
T2:种在序列上,线段树?区间查询?我想的是把每个点初始化成负权值,然后可以区间修改,区间查询。然鹅发现可以二分,二分竟然是错的。确实不满足单调性。k<=1?不会码,自己好垃圾。最终只拿了20分(好吧,r的初始值也没想对)。正解是数论分块,听起来很高大上,但其实就是分段函数。神犇的soul竟然AK了,%一波。其实要是拍一波,感脚自己还是可以发现问题的。

1 #include<cstdio>
2 #include<iostream>
3 #define MAXN 110
4 #define ll long long
5 using namespace std;
6 inline ll read(){
7 ll s=0;
8 char ch=getchar();
9 while(ch<'0'||ch>'9')ch=getchar();
10 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
11 return s;
12 }
13 inline ll maxn(ll a,ll b){
14 return a>b?a:b;
15 }
16 ll l,r;
17 ll n,k;
18 ll rn[MAXN];
19 inline ll xs(ll a,ll b){
20 ll lin=a/b;
21 if(lin*b==a)return lin;
22 else return lin+1;
23 }
24 bool pd(ll d){
25 // printf("orz d=%d\n",d);
26 ll js=k;
27 for(int i=1;i<=n;++i){
28 // printf("QAQ i=%d\n",i);
29 // printf("x=%d duo=%d\n",xs(rn[i],d),xs(rn[i],d)*d-rn[i]);
30 js-=xs(rn[i],d)*d-rn[i];
31 if(js<0)return false;
32 }
33 if(js<0)return false;
34 return true;
35 }
36 int main(){
37 // freopen("da.in","r",stdin);//!!!!!!!!!!!shan
38 n=read();k=read();
39 for(int i=1;i<=n;++i){
40 rn[i]=read();
41 r=maxn(rn[i],r);
42 // printf("rn[%d]=%d\n",i,rn[i]);
43 }
44 l=1;
45 while(r-l>1){
46 ll mid=l+r>>1;
47 if(pd(mid))l=mid;
48 else r=mid;
49 // printf("l=%d r=%d\n",l,r);
50 }
51 if(pd(r))printf("%lld\n",r);
52 else printf("%lld\n",l);
53 }
54 /*
55 wan na kai ll
56 gaodu bu di yu!!!!!
57 zhi hou zhe ke shu miao bu zai zhang gao???
58 20% k<=1
59 qi ta erfen ?
60 */
对拍可以解决低错,还有特殊情况,要重视
T3:超级树?无限懵比,考虑暴搜,建图就要画不少时间。尽管优化了两层循环,但是k==6仍然跑不粗来。而且考试中取模去错了,毒瘤出题人竟然造了1%1的数据,天!正解DP很神,为了保证不相交,状态自带BUFF,三层循环就跑粗来了!!!不过情况很多,真让人头大。wd orz,让我看懂了题解,受益匪浅。

1 #include<cstdio>
2 #include<vector>
3 #include<iostream>
4 #include<cstring>
5 #define ll long long
6 using namespace std;
7 inline int read(){
8 int s=0;
9 char ch=getchar();
10 while(ch<'0'||ch>'9')ch=getchar();
11 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
12 return s;
13 }
14 vector<int >bl[1<<11|1];
15 int k,mod,root;
16 ll ans;
17 int MOD(int a){
18 return a<mod?a:(a-mod);
19 }
20 bool fw[1<<11|1];
21 int sum;
22 void dfs(int u,int len){
23 // printf("u=%d len=%d\n",u,len);
24 if(len==(1<<k)){
25 return ;
26 }
27 sum=(sum+1)%mod;
28 fw[u]=true;
29 for(int k=0;k<bl[u].size();++k){
30 if(fw[bl[u][k]])continue;
31 dfs(bl[u][k],len+1);
32 }
33 fw[u]=false;
34 return ;
35 }
36 int hai[101],ncnt[101];
37 void init(int u,int sd){
38 ++ncnt[sd];
39 hai[sd]=u;
40 if(sd==k)return ;
41 init((u<<1),sd+1);
42 init((u<<1|1),sd+1);
43 for(int k=0;k<bl[u<<1].size();++k){
44 bl[u].push_back(bl[u<<1][k]);
45 bl[bl[u<<1][k]].push_back(u);
46 }
47 for(int k=0;k<bl[u<<1|1].size();++k){
48 bl[u].push_back(bl[u<<1|1][k]);
49 bl[bl[u<<1|1][k]].push_back(u);
50 }
51 bl[u].push_back(u<<1);bl[u].push_back(u<<1|1);
52 bl[u<<1].push_back(u);bl[u<<1|1].push_back(u);
53 return ;
54 }
55 int cc;
56 int main(){
57 // freopen("da.in","r",stdin);
58 k=read();mod=read();
59 if(k==1){
60 printf("%d\n",1);
61 return 0;
62 }
63 if(k==2){
64 printf("%d\n",(11%mod));
65 return 0;
66 }
67 if(k==3){
68 printf("%d\n",(353%mod));
69 return 0;
70 }
71 if(k==4){
72 printf("%d\n",(185623%mod));
73 return 0;
74 }
75 if(k==5){
76 printf("%d\n",(464391539%mod));
77 return 0;
78 }
79 ans=((1<<k)-1)*1ll;
80 init(root=1,1);
81 for(int sd=1;sd<=k;++sd){
82 dfs(hai[sd],0);
83 ans=(ans+sum*ncnt[sd]%mod)%mod;
84 sum=0;
85 // printf("%lld\n",ans);
86 }
87 printf("%lld\n",ans%mod);
88 }
89 /*
90 wa na wa na da biao=fail
91 40% k<=10 da biao
92 fa xian tongyi shendu de tong yi len de xianranxiang tong
93 */
其实像这种题,保证卡完送分点就可以弃掉了,除非T1,T2也很难。
2019/7/22
rank42/56
考自闭了,只谈谈注意事项吧
T1:没有考虑清楚所有可特判的情况,exgcd的理解不透,板子会码,然而不明白算出来的不是最小解。
T2:交了个CE!!!!!暴搜思路对了,尚不清楚哪里出错了
T3:没时间了,emmm,没有注意墙可以反弹...
心态爆炸,考试中途一小时gedit白了,????,被迫用了guide,总之这次比较失败。相信这次失误下次不再犯。
希望下次能Burning like a fire gone wild on Saturday.
2019/7/25
rank47/56
emmm,这回题挺水的,但,我脑子抽了,一心认为自己能刚掉第二题,赌注不能押啊,第一题基本全A,我竟然跳了!!!
反思,反思,反思
2019/7/27

rank7/56
T1:刚开始模样例,其实是发现了样例有问题的,但出于往昔大量刷题自己样例经常模错的经验,没有勇敢的去询问。(其实这种事值得反思,姑且不说早点问清能多留时间骗几分,这是一种天将降大任于斯人的责任感),试想,如果这是在正式比赛,因一个样例弃掉几分该有多么可惜。第一题的问题还不只这些,其实无脑QJ是可以搞到20分的,然鹅(没时间,还是刚才的锅)没有想到先把n个数取mod再计算,导致没看出来mod==2的送分数据。
T2:至少能想到的骗分方法都搞了,还可以,但是v=u+1的数据不知道为啥没苟到。但做这题的问题在于没往DP上想!!!!DP意识仍然不够,感觉自己O(n^2)预处理高斯消元就可以了,自己还是太LJ了。
T3:留给这道题的时间不足,导致没AK,而且忘了输样例和rand数了。输样例还真得了5分!!!!0情况,原题,1情况,卡特兰数(bb老师所说的考试出的卡特兰,没想到这么水,卡特兰专题没咋刷的我hhh)2情况,因时间不够,总感觉只要一个式子就搞出来了,也就没在最后10分钟里将就DP。3情况,还是卡特兰。
UPD:T3情况2的dp,考试时想的是如果往上走再回来,只考虑一次,emmm,显然是错的。可以来回好几次的,考虑dp[i]表示走了i步会原点的方案数。dp[i]=4×sigma(dp[i-j]*ktl(j/2-1))(j&1==0)。解释一下,减少一维表示第几次回原点(比较像背包)。中间分配(j/2-1)步去走1点的卡特兰数,这样才能不算重。因为坐标轴有四个方向,乘四。
只是题水,侥幸拿了好名次,希望后天能Guess won't be coming to church on Sunday.
2019/7/29

rank24/55
考试心态爆炸,前两个小时基本没拿到分,第二题暴力挂了,第一题暴力没码
T1:氢键?又是大模拟题,估计又是什么桶啥的。于是乎,在手玩了几组数据后发现所有氢键都可以表示成斜率为+1,-1的直线的贡献,斜率为正负一,等等,这不就是<光>吗,开vector存(x+y)和(x-y)。贼开心,以为自己是正解,开开心心的码,码着码着,发现坐标范围1e9,昂?????!!!!!这怎么开得了,沉思,一定是有什么奇技淫巧的办法优化,我应该过一会就能想出来了,然后跳了。emmm,最后永远的弃了。考完发现7个dalaoA掉了,就是n^2模拟!!!!没注意n的范围,不应该啊。
T2:这题很像雨天的尾巴,再扫一眼,嗯,连lca都不用求了。动态开点码了一半,发现不对劲,直接差分好像行不通,因为节点存的个数限制,差分需要考虑change的时间顺序。这估计到正解了吧~~花了半个小时码完,死活調不粗来,开了下时间还有40分钟,随便丢了个能过大样例的暴力上去,结果WA10 QwQ
T3:还剩40分钟,发现前两个小时基本没捞到分,心中暗想,就靠T3了,读错了四遍题,最后发现还挺好推的,但是方案数是暴搜出来的,容斥最后十分钟死活搞不粗来,太没出息了,别人都95,我55,下来问了zzyy,发现这么简单,(i^k-(i-1)^k)就是减去不合法的最后的方案数了,唉,还是太菜。。。
T2接近正解,T3正解不会容斥,这都是很可惜的,代码能力仍需提高,希望Tuesday I was through hoping.
2019/8/1
rank38/52
炸了,这次题比较难,三个暴力就能rank7,问题主要是暴力码不对
T1:10min打完快排,又码了个归并(明明都是O(n*logn)),桶排也没能跑得飞快,正解桶排+线段树优化还是很棒的。
T2:20分暴力没拿到,还白白浪费一个多小时,出题人根本没给清题干,导致样例模不过去。正解dp+奇袭的序列问题思想,该反思的是很像奇袭一题离得每列至多有一个1的思想没有想到,说明考试反思分析不太够。%%wjnAK了这道题。
UPD:mblj的dp,先%lnc,主要是dp的状态很神,在保证左区间合法性的同时维护右区间。
#include<cstdio>
#include<iostream>
#define MAXN 3010
#define int long long
using namespace std;
const int mod=998244353;
int dp[MAXN][MAXN];
int lsm[MAXN],rsm[MAXN];
int n,m;
int MOD(int a){
return a<mod?a:(a-mod);
}
int inv[MAXN],inv_jc[MAXN],jc[MAXN];
void init(){
inv[1]=inv_jc[1]=jc[1]=1ll;
inv_jc[0]=jc[0]=1ll;
for(int i=2;i<=m;++i){
jc[i]=jc[i-1]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
inv_jc[i]=inv_jc[i-1]*inv[i]%mod;
//cout<<jc[i]<<" "<<inv[i]<<" "<<inv_jc[i]<<endl;
}
}
int A(int n,int m){
if(m>n)return 0;
return jc[n]*inv_jc[n-m]%mod;
}
signed main(){
// freopen("da.in","r",stdin);
scanf("%lld%lld",&n,&m);
for(int i=1,a,b;i<=n;++i){
scanf("%lld%lld",&a,&b);
++lsm[a];++rsm[b];
}
init();
for(int i=1;i<=m;++i)lsm[i]+=lsm[i-1];
for(int i=1;i<=m;++i)rsm[i]+=rsm[i-1];
int base;
dp[1][0]=1;
dp[1][1]=rsm[1];
for(int i=1;i<m;++i){
for(int j=0;j<=i;++j){
base=A(i-j-lsm[i-1],lsm[i]-lsm[i-1]);
if(!base)continue;
dp[i+1][j]=(dp[i+1][j]+dp[i][j]*base%mod)%mod;
dp[i+1][j+1]=(dp[i+1][j+1]+dp[i][j]*(rsm[i+1]-j)%mod*base%mod)%mod;
}
}
/*for(int i=1;i<=m;++i)
for(int j=1;j<=m;++j)
printf("dp[%lld][%lld]=%lld\n",i,j,dp[i][j]);*/
printf("%lld\n",dp[m][n]%mod);
}
T3:暴力40,我拿了30,原因是竟然有0 0的数据,然而我的程序默认a[1]=read(),emmm...题中给的一坨操作就是逻辑左移(不会,我没脸)。逻辑左移就是先左移一位,高位去掉补成0位。
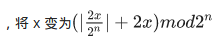
分析一下为什么,2*x就是左移一位,(2*x/2^n)就是最高位,两个相加再mod2^n去掉了最高位。妙~啊~
于是问题实质对手的操作就是使x和qsm[i]都左移,再异或后缀和。转化成把[0,2^n)中的数(因为逻辑左移后仍然属于这个区间),异或给m+1个数。可以考虑开trie,贪心。当节点u只有一个儿子,我们有办法把它变成1,而对手只能干看着。如果有两个节点,那么,我们虽然有办法使其为1,但无论怎样对手都能让它为0,值不改变,但两个方向都要跑一遍。O(n*m)
#include<cstdio>
#include<iostream>
#define MAXN 100010
#define int long long
using namespace std;
inline int read(){
int s=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s;
}
#define kd (read())
int n,m;
int ans=-1,cnt;
int qsm[MAXN];
int bin[31];
struct trie{
trie *tr[2];
}*root;
trie *nwt(){
trie *tmp=new trie;
for(int i=0;i<2;++i)tmp->tr[i]=NULL;
return tmp;
}
void insert(int a){
trie *tmp=root;
for(int i=n-1;i>=0;--i){
int idx=((a&bin[i])!=0);
if(tmp->tr[idx]==NULL)tmp->tr[idx]=nwt();
tmp=tmp->tr[idx];
}
}
void dfs(trie *tmp,int res,int base){
if(!base){
if(res>ans)ans=res,cnt=1;
else if(res==ans)++cnt;
return ;
}
bool k1,k2;
k1=(tmp->tr[0]!=NULL);
k2=(tmp->tr[1]!=NULL);
if(k1&&k2){dfs(tmp->tr[0],res,base>>1);dfs(tmp->tr[1],res,base>>1); }
else if(k1)dfs(tmp->tr[0],res+base,base>>1);
else if(k2)dfs(tmp->tr[1],res+base,base>>1);
return ;
}
signed main(){
// freopen("da.in","r",stdin);
bin[0]=1;
n=kd;m=kd;
for(int i=1;i<=n;++i)
bin[i]=bin[i-1]<<1;
for(int i=1,a;i<=m;++i){
a=kd;
qsm[i]=qsm[i-1]^a;
}
root=nwt();
int lres;
for(int i=0;i<=m;++i){
lres=(qsm[i]<<1)%bin[n]+(qsm[i]>>(n-1));
lres^=qsm[m]^qsm[i];
insert(lres);
}
dfs(root,0,bin[n-1]);
printf("%lld\n%lld\n",ans,cnt);
}
低错需要避免,暴力需要走心。。。
2019/8/3

rank48/64
原地爆炸。。。
T1:很明显的性质,考场上画了几个图就搞出来了,瞬间脑抽,感觉硬扫不行(你明明都没算),去搞连数组都开不下的树上倍增,结果就是硬扫。实质上是时间复杂度没有计算。达到10^12的费波那契为60,我们找到的性质是此点减去最大的比他小的费波那契为他的直接祖先。那么其实不用建图,n询问,一次最多60×log60,为O(n*60*log60),小得很好吗!!(竟然还有sb码完正解去加个树上倍增雾)1s大概跑1e8。。。clock()1s为1e6
T2:本来以为是分块原题,发现问的不太一样,想瞎搞一个动态开点的桶线段树,但就是感觉开不下,然后把正解做法弃了!!去码带修莫队,没学过,码的莫队骗分,脑子乱了。正解的vector比较强(高级数据结构真TM学傻了),直接开桶vector排序,二分查找。可能会对修改有疑惑,考虑a[x]==a[x+1],无影响。a[x]!=a[x+1],在桶中的排序无影响,只该对应位置即可,O(n*logn),加STL,小常数跑得飞快。
T3:10min码了个printf("1\n\n")骗了4分,实在没时间了。正解贪心+二分图判定。首先可证明贪心是正确的。倒序枚举能和前面合并就合并,因为和前面枚举的合并不吃亏,但和后面枚举的合并可能会有负贡献。能保证m最小,字典序最小。K=1的情况就解决了,K=2时,考虑判断条件改变,因为可以分两组(和关押罪犯很像),有矛盾的一定要分开,那么不合法的情况为a与b有矛盾,b与c有矛盾,c与a有矛盾。实质是判二分图,染色和并差集都可以,但特判挺坑人的(在代码里标记了)
#include<bits/stdc++.h>
#define MAXN 600000
#define int long long
using namespace std;
inline int maxn(int a,int b){return a>b?a:b; }
inline int read(){
int s=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s;
}
#define kd (read())
int n,K;
int a[MAXN];
int sc[MAXN];
int mp[MAXN];
int zmx,ad;
int fat[MAXN];
int find(int x){
if(!fat[x]||fat[x]==x)return x;
return fat[x]=find(fat[x]);
}
inline void merge(int x,int y){
fat[find(x)]=find(y);
return ;
}
void case_1(){
int m=0;
++m;
mp[a[n]]=1;
sc[++sc[0]]=n;
for(int i=n-1;i>=1;--i){
bool ok=0;
for(int x=zmx;x*x>=a[i];--x)
if(mp[x*x-a[i]]){ok=1;break;}
if(ok){
++m;
sc[++sc[0]]=i;
for(int j=i+1;j<=sc[sc[0]-1];++j)mp[a[j]]=0;
mp[a[i]]=1;
continue;
}
mp[a[i]]=1;
}
printf("%lld\n",m);
for(int i=sc[0];i>=2;--i)printf("%lld ",sc[i]);
puts("");
}
int dd[MAXN];
bool vis[MAXN];
bool gen[MAXN];
void case_2(){
for(int i=2;i<=512;++i)/////////
if(!((i*i)&1))gen[i*i/2]=1;//////////
int m=0;
++m;
mp[a[n]]=1;
sc[++sc[0]]=n;
for(int i=n-1;i>=1;--i){
bool ok=0;
int tmp;
for(int x=zmx;x*x>=a[i];--x)
if(mp[tmp=x*x-a[i]]){
if(tmp==a[i]){
if(mp[a[i]]==2){ok=1;break; }///////
if(vis[a[i]]){ok=1;break; }/////////
merge(a[i],a[i]+ad);
continue;
}
if(tmp!=a[i]){
vis[a[i]]=1;
if(gen[a[i]]&&mp[a[i]]==2){ok=1;break; }//////
if(gen[tmp]&&mp[tmp]==2){ok=1;break; }////////
merge(a[i],tmp+ad);//////
merge(a[i]+ad,tmp);//////
if(find(a[i])==find(a[i]+ad)||find(tmp)==find(tmp+ad)){ok=1;break; }////
continue;
}
}
//if(mp[a[i]]>=3)ok=1;
if(ok){
++m;
sc[++sc[0]]=i;
for(int j=i;j<=sc[sc[0]-1];++j){mp[a[j]]=fat[a[j]]=fat[a[j]+ad]=vis[a[j]]=0;}
mp[a[i]]=1;//////////
continue;
}
++mp[a[i]];//////
}
printf("%lld\n",m);
for(int i=sc[0];i>=2;--i)printf("%lld ",sc[i]);
puts("");
}
signed main(){
//freopen("division23.in","r",stdin);
//freopen("1.out","w",stdout);
n=kd;K=kd;
for(int i=1;i<=n;++i)a[i]=kd,zmx=maxn(zmx,a[i]);
ad=zmx*2;
zmx=sqrt(zmx*2);
if(K==1){case_1();return 0; }
if(n==2){printf("1\n\n");return 0; }
else case_2();
return 0;
}
只希望先到正解的题能AK,话说tkjTQL。
2019/8/5

rank18/63
最近考试总是没自信啊~~,七次考试结束了,不出所料的没进第一机房,回顾之前考试,加上能拿到的分名次还是可以的。时间分配也不行,好几次T3的暴力都码不完。
2019/8/7

rank22/62
咕了
2019/8/9

rank40/56
不知为何,一有送分题就要崩
T1:一眼容斥,其实容斥不会,推了一个至少不符合的天为s个队的不合法情况,不对啊!!正解是至少有s天不符合,而不去管怎样不符合。
有C(n,i)*C(m-i*k-1,n-1),本身只是挡板法,减去i×k是钦定了谁一定为不符合。本来码了70%暴力,细节下标为负处理不当,WA30,考试过程中思路趋向了用倍增优化,但时间复杂度显然不是优化。。。
T2:sb题,题意不明。就不诉苦错误思路了。正解是缩点+最长链,因为一个联通图一轮最多一个爆炸,所以最长链是能覆盖所有其他链的答案,因此为最长链。
T3:好难,概率DP真糟心,暴力不太会码。。。
总感觉T1可A,于是刚了一整场考试,人不能太固执。
2019/8/11

rank16/51
太弱了,这是第几次贪心看不出来,桶想不出来,好虚啊~~
T1:n^4的暴力很好想,能拿75分,方向找对,正解也不难,我们可以利用取模的性质,当两个数在模m的意义下同余,那么两个数做差即可整除m。考虑如何运用到大模拟中,我们可以发现冗余的部分时在不同的矩形中,相同的位置可能重复计算,而且不能产生贡献的矩阵的信息直接扔掉了。此时可以利用这些看似无用的信息来得出其他有用的答案。此时可以枚举行的上边界和下边界,列从1一层层扩展,记录每个(i1,1,i2,j)的矩阵模k的余数,放在桶里,统计答案查相同的余数(相当于作差的操作)。从++到+=tong[],为O(n^2*m)

1 #include<cstdio>
2 #include<iostream>
3 #include<vector>
4 #include<cstring>
5 #define reg register
6 #define MAXN 1010
7 #define ll long long
8 using namespace std;
9 inline ll read(){
10 ll s=0;char ch=getchar();
11 while(ch<'0'||ch>'9')ch=getchar();
12 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
13 return s;
14 }
15 #define kd (read())
16 ll n,m,k;
17 ll qsm[MAXN][MAXN];
18 ll jz[MAXN][MAXN];
19 ll tong[1000100];
20 vector<int >dd;
21 bool pd[1000100];
22 void case_1(){
23 if(!(jz[1][1]%k)){
24 ll ans=0;
25 for(reg ll i=1;i<=n;++i)
26 for(reg ll j=1;j<=m;++j)
27 ans+=(1ll*(n-i+1)*(m-j+1));
28 printf("%lld\n",ans);
29 return ;
30 }
31 ll ans=0;
32 for(reg ll i=1;i<=n;++i)
33 for(reg ll j=1;j<=m;++j)
34 if((1ll*i*j*jz[1][1])%k==0)
35 ans+=(1ll*(n-i+1)*(m-j+1));
36 printf("%lld\n",ans);
37 return ;
38 }
39 ll cal(int i1,int j1,int i2,int j2){
40 return qsm[i2][j2]-qsm[i2][j1-1]-qsm[i1-1][j2]+qsm[i1-1][j1-1];
41 }
42 int main(){
43 //freopen("da.in","r",stdin);
44 n=kd;m=kd;k=kd;
45 ll rn;
46 bool pd_same=1;
47 for(reg ll i=n;i>=1;--i)
48 for(reg ll j=1;j<=m;++j){
49 jz[i][j]=kd;
50 if(i==n&&j==1)continue;
51 if(j>1&&jz[i][j]!=jz[i][j-1])pd_same=0;
52 else if(j==1&&jz[i][1]!=jz[i+1][m])pd_same=0;
53 }
54 for(reg ll i=1;i<=n;++i)
55 for(reg ll j=1;j<=m;++j)
56 qsm[i][j]=qsm[i][j-1]+qsm[i-1][j]-qsm[i-1][j-1]+jz[i][j];
57 if(pd_same){
58 case_1();
59 return 0;
60 }
61 ll ans=0;
62 /*for(reg ll il=1;il<=n;++il)
63 for(reg ll jl=1;jl<=m;++jl)
64 for(reg ll i=il;i<=n;++i)
65 for(reg ll j=jl;j<=m;++j)
66 if(!cal(il,jl,i,j))
67 ++ans;*/
68 for(reg ll i1=1;i1<=n;++i1)
69 for(reg ll i2=i1;i2<=n;++i2){
70 for(reg ll j=1;j<=m;++j){
71 ll tt=cal(i1,1,i2,j)%k;
72 //cout<<i1<<" "<<1<<" "<<i2<<" "<<j<<endl;
73 //cout<<tt<<endl;
74 if(tt==0)++ans;
75 ans+=tong[tt];
76 ++tong[tt];
77 if(pd[tt])continue;
78 pd[tt]=1;
79 dd.push_back(tt);
80 }
81 while(!dd.empty()){
82 pd[dd[dd.size()-1]]=0;
83 tong[dd[dd.size()-1]]=0;
84 dd.pop_back();
85 }
86 //memset(tong,0,sizeof(tong));
87 }
88 printf("%lld\n",ans);
89 }
T2:码了k==1的dp+一堆特判(dp码错了),正解就是个贪心!!!还很好证,水题都做不粗来了,QAQ555。具体操作是将节点塞到堆里,按深度排序,每次取堆顶,在它的K级父亲点亮。
伪证明:对于一个叶子来说,点亮叶子一定会比点亮它的父亲要劣,点亮它的祖先随着深度减小,决策是单调不下降的,而且距离叶子越近,浪费的长度越多。

1 #include<cstdio>
2 #include<iostream>
3 #include<vector>
4 #include<cstdlib>
5 #include<queue>
6 #define MAXN 200100
7 #define reg register
8 #define INF (1<<30)
9 using namespace std;
10 inline int maxn(int a,int b){return a>b?a:b; }
11 inline int minn(int a,int b){return a<b?a:b; }
12 inline int read(){
13 int s=0;char ch=getchar();
14 while(ch<'0'||ch>'9')ch=getchar();
15 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
16 return s;
17 }
18 #define kd (read())
19 struct rr{
20 int nt,to;
21 }bl[MAXN<<1];int hd[MAXN],itot;
22 void add(int x,int y){
23 bl[++itot].to=y;
24 bl[itot].nt=hd[x];
25 hd[x]=itot;
26 }
27 int n,k,t;
28 priority_queue<pair<int ,int > >dd;
29 int fat[MAXN];
30 bool fg[MAXN];
31 void _dfs(int u,int fa,int sd){
32 dd.push(make_pair(sd,u));
33 fat[u]=fa;
34 for(reg int i=hd[u];i;i=bl[i].nt){
35 if(bl[i].to==fa)continue;
36 _dfs(bl[i].to,u,sd+1);
37 }
38 }
39 int ans=0;
40 bool vis[MAXN];
41 void _work(int u,int cnt,int _sn){
42 if(vis[u])return ;
43 if(!u||!cnt)return ;
44 fg[u]=1;
45 //cout<<u<<" "<<cnt<<" "<<endl;
46 vis[u]=1;
47 _work(fat[u],cnt-1,u);
48 for(reg int i=hd[u];i;i=bl[i].nt)
49 if(bl[i].to!=fat[u]&&bl[i].to!=_sn)
50 _work(bl[i].to,cnt-1,0);
51 vis[u]=0;
52 }
53 int zhao(int u,int cnt){
54 while(u&&cnt){
55 u=fat[u];
56 --cnt;
57 }
58 return u;
59 }
60 int main(){
61 //freopen("da.in","r",stdin);
62 n=kd;k=kd;t=kd;
63 for(reg int i=1,u,v;i<n;++i){
64 u=kd;v=kd;
65 add(u,v);add(v,u);
66 }
67 _dfs(1,0,1);
68 while(!dd.empty()){
69 while(!dd.empty()&&fg[dd.top().second])dd.pop();
70 if(dd.empty())break;
71 //cout<<zhao(dd.top().second,k)<<endl;
72 _work(zhao(dd.top().second,k),k+1,0);
73 dd.pop();
74 ++ans;
75 }
76 printf("%d\n",ans);
77 }
T3:假贪心暴搜骗了20分,其实特判送了不少分。这题有点意思,差分+状压dp
沾个唯一看懂的题解

1 考虑正解:
2
3 首先我们知道异或满足差分的性质:可逆性
4
5 从本质上来说,异或就是取反的过程,所以正过来可以,反过去也是可以了
6
7 这样就把一段区间取反转化为端点取反了。
8
9 问题转化为:
10 给定一个长度为n的0-1序列,最多包含2k个1,每次可以把间隔一定长度的两个位置取反,求最少多少次把序列全部变成0
11
12 然后我们发现,肯定是要对1操作的,不可能平白无故地把两个0取反(尽管最后的结果与操作顺序无关,但这里考虑下操作顺序)
13
14 如果是1和0的话,就可以看成1转移到了0的位置并花费了一次操作的代价
15
16 如果是1和1的话,就可以看成1转移到了另一个1的位置,然后两个1都消去了并花费了一次操作的代价
17
18 这样问题转化为:
19 给定一个长度为n的0-1序列,最多包含2k个1,每次可以把1转移到相距一定长度的位置,如果两个1在同一位置就会消去,求最少多少次把序列全部变成0
20
21 进一步转化为:
22 给定一个n个节点的图,其中最多2k的节点有物品,每次可以把一件物品转移到相距一定长度的位置,如果一个节点出现两个物品就会消去,求最少多少次把物品全部消除
23
24 我们可以用2k次bfs处理出每个物品与另外所有物品消去的代价,
25
26 这样问题转化为:
27 给定2k个物品,其中每2个物品消去都会消耗一定的代价,求把所有物品消去的最小代价
28
29 这样就是状压dp了,可以用SPFA来解决
差分以优秀的O(1)解决了区间修改,注意考虑范围,k很小是突破口,差分序列1和1撞在一起抵消很神

1 #include<bits/stdc++.h>
2 #define INF (1<<30)
3 using namespace std;
4 inline int minn(int a,int b){return a<b?a:b; }
5 inline int read(){
6 int s=0;char ch=getchar();
7 while(ch<'0'||ch>'9')ch=getchar();
8 while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
9 return s;
10 }
11 #define kd (read())
12 int n,k,m;
13 int num;
14 int ys[40010];
15 bool pd[40010];
16 int cost[20][20];
17 int dp[1<<17];
18 int cz[40010];
19 vector<int >dd;
20 bool vis[40010];
21 queue<pair<int ,int > >td;
22 void bfs(int x){
23 while(!td.empty())td.pop();
24 memset(vis,0,sizeof(vis));
25 td.push(make_pair(x,0));
26 //vis[x]=1;
27 int tto;
28 int js=num;
29 while(!td.empty()&&js){
30 int ltop=td.front().first,base=td.front().second;td.pop();
31 for(int i=1;i<=m;++i){
32 tto=cz[i]+ltop;
33 if(tto<=n+1&&!vis[tto]){
34 if(ys[tto]){
35 cost[ys[x]][ys[tto]]=base+1;
36 --js;
37 }
38 vis[tto]=1;
39 td.push(make_pair(tto,base+1));
40 }
41 tto=ltop-cz[i];
42 if(tto>=1&&!vis[tto]){
43 if(ys[tto]){
44 cost[ys[x]][ys[tto]]=base+1;
45 --js;
46 }
47 vis[tto]=1;
48 td.push(make_pair(tto,base+1));
49 }
50 }
51 }
52 }
53 int main(){
54 //freopen("da.in","r",stdin);
55 memset(cost,-1,sizeof(cost));
56 n=kd;k=kd;m=kd;
57 for(int i=1,a;i<=k;++i){
58 a=kd;
59 /*ys[a]=++num;
60 dd.push_back(a);
61 ys[a+1]=++num,dd.push_back(a+1);*/
62 pd[a]^=1;pd[a+1]^=1;
63 }
64 for(int i=1;i<=n+1;++i)
65 if(pd[i]){
66 ys[i]=++num;
67 dd.push_back(i);
68 }
69 for(int i=1;i<=m;++i)
70 cz[i]=kd;
71 //sort(cz+1,cz+m+1);
72 for(int k=0;k<dd.size();++k){
73 bfs(dd[k]);
74 //cout<<dd[k]<<" "<<ys[dd[k]]<<endl;
75 }
76 /*for(int i=1;i<=num;++i)
77 for(int j=1;j<=num;++j)
78 cout<<i<<" "<<j<<" "<<cost[i][j]<<endl;*/
79 int lim=(1<<num)-1;
80 for(int st=lim-1;st>=0;--st)
81 dp[st]=INF;
82 dp[lim]=0;
83 for(int st=lim;st>=1;--st){
84 if(dp[st]==INF)continue;
85 for(int w1=0;w1<num;++w1)
86 if((1<<w1)&st)
87 for(int w2=0;w2<num;++w2)
88 if(w1!=w2&&((1<<w2)&st)&&cost[w1+1][w2+1]!=-1)
89 dp[st^(1<<w2)^(1<<w1)]=minn(dp[st^(1<<w2)^(1<<w1)],dp[st]+cost[w1+1][w2+1]);
90 }
91 printf("%d\n",dp[0]);
92 return 0;
93 }
我好菜啊,找准自己的位置不意味着低下头地承认自己的位置。
2019/8/12

rank47/50
2019/8/13AM

rank18/50
2019/8/13PM
rank35/56
2018/8/14

rank34/58
2018/8/15
rank14/49
我告诉你,你是输过几次,但你还能东山再起
2019/8/16
rank9/52
T1:中等水,不算太水
T2:暴力分很足,正解优化思想
T3:没时间草草码了暴力,过了样例就扔上去了,然而其实可以过掉50分,正解的容斥不算太难
清醒,清醒
2019/8/17

rank26/54
其实名次不怎么好,题难点,分差不大,但oi是看名次的,暴力依旧没能打满。。。
————————————————————————————————
分A,B卷了,B卷做得gou_sei一样
2019/8/18
rank31/36
2019/8/19
rank16/36
2019/8/20
rank7/46
2019/8/21
rank10/42
2019/8/22
rank8/30
2019/8/23AM
rank27/30(爆零了,B卷爆零)
2019/8/23PM
rank9/45
2019/8/28
rank9/45
莫名其妙地苟到了一机房,惊!!!!问题暴露很充分,B卷基本没满意过,还爆零一回,也就是靠着统一卷并不难的BUFF拿了几次前十,正解基本没怎么想到过,全是暴力打满。还是要多思考,再不想正解,留退役后再想吗?
2019/8/29
rank11/45

不太妙,T1 1e12 qpow卡掉了10分,T2 10分忘码了,T3纯粹骗分,T2,T3都是好题
注意脚下
2019/9/1
rank10/45
2019/9/2
rank19/45

2019/9/3
rank3/45
获得成就,人生中第一个小绿框,第一次进前三。
没啥可说的,题并不难,拿到这个成绩靠了很大运气,不奢求保持,只希望之后考试心态继续保持
Sunset Juses,don"t let me down.



