【论文学习3】Local Differential Privacy for Deep Learning
Local Differential Privacy for Deep Learning
0.ABSTRACT
-
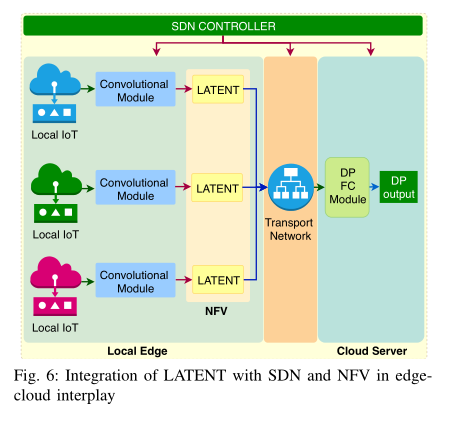
物联网平台创新包括边缘云交互中的软件定义网络(SDN)和网络功能虚拟化(NFV)的融合
-
深度学习因其在使用大量数据进行训练时具有显著的准确性而越来越受欢迎。然而,当使用高度敏感的众包数据(如医疗数据)进行训练时,DL算法往往会泄露隐私。
-
我们提出了一种新的局部差异私有(LDP)算法,称为LATENT算法,重新设计了训练过程。LATENT允许数据所有者在数据离开设备之前添加随机化层.卷积神经网络的结构被划分为:(1)卷积模块(2)随机化模块(3)全连接层。随机化模块可以作为NFV隐私保护服务运行。
-
随机化模块中采用了一种新的LDP协议,称为效用增强随机化(utility enhanced randomization),与现有的LDP协议相比,它允许潜在用户保持较高的效用。我们对潜在卷积深度神经网络的实验评估表明,即使在低隐私预算(例如,ε=0.5)下,具有高模型质量的优良精度。
1.introdution
在论文中,我们:
- examine the privacy issues of deep learning
- develop a distributed privacy-preserving mechanism using DP to control and limit privacy leaks in deep learning
contribution(a distributed LDP mechanism with a new LDP protocol )
- 提出的新算法(LATENT)应用了随机响应的属性——LDP设置和算法的层结构可以使得在不同层级进行隐私保护交流
- 设计了一种新的协议,称为效用增强随机化(UER)
(1)首先对优化的一元编码协议(OUE)进行了改进,提出了一种新的LDP协议modified OUE(MOUE),增强了二进制字符串随机化的灵活性。
(2)OUE是一个LDP协议,遵循随机1和0的不同直觉,以提高效用。
(3)MOUE通过引入一个额外的系数α(隐私预算系数)来实现改进的灵活性,该系数在选择随机化概率时提高了灵活性。 - 然后我们遵循MOUE背后的动机,提出了在高灵敏度的长二进制字符串随机化过程中保持效用的UER。
2.background
2.1 Differential Privacy
DP定义了在数据集中可能被泄露给对手的信息界限,ε (epsilon) and δ (delta) 被用来表示这些界限。
1)Privacy budget / privacy loss (ε)
隐私损失ε可以观察DP算法中的隐私泄露。ε越高,隐私泄露越多。
2)Probability to fail / probability of error (δ)
δ用来计算可能导致高隐私损失的事件。δ是输出显示特定个体身份的概率,可能会发生δn次(n为记录数)。为了最小化隐私损失,δn必须保持一个最小值。
3)Definition of differential privacy

2.2 Global vs. Local Differential Privacy
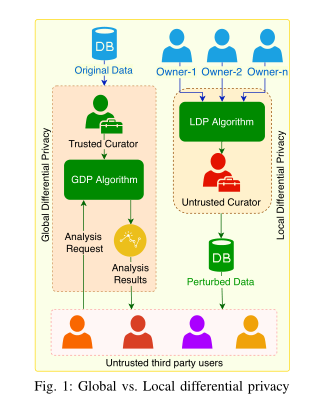
GDP需要一个可信第三方来对真实结果加噪音然后返回给请求者,最常用的机制是Laplace机制和Gaussian机制
LDP不需要可信第三方,数据在传给第三方之前就已经进行随机化

2.3 Random Response(随机响应)
随机响应通过随机化结果“是”或“否”的回答来消除逃避型的答案偏差。通常是用硬币来决定的,如果是正面朝上,回答真实结果;如果翻面朝上,就回答相反结果。提供真实结果的概率为p,当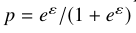 满足ε—differentital privacy
满足ε—differentital privacy
2.4 Sensitivity, Privacy Budget (ε), and Determination of the Probability (p) of Randomization
为了量化传输比特串的LDP过程中的随机化概率p,我们可以使用随机聚合隐私保护顺序响应RAPPOR,这是google提出的LDP算法。RAPPOR是从离散数据字典中估计字符串的客户端分布。
灵敏度定义为单个个体对查询结果的最大影响。任意函数f,灵敏度∆f为:

RAPPOR是一个LDP算法。在全局灵敏度定义中,x和y为相邻输入。在RAPPOR算法中,任何输入vi都被编码成d比特的向量,每个d比特向量都包含d-1个0和1个1,所以∆f的最大值为2比特。换句话说,RAPPOR的灵敏度f为2.

2.5Properties of Differential Privacy
- Postprocessing invariance/robustness(后处理不变形/稳健性)
在差分隐私算法中会有一些额外的计算,但这些计算并不会削弱隐私保证,对ε—DP的额外计算结果仍满足ε—DP。
- quantifiability(可量化性)
可量化性是指在随机化过程中计算精确扰动提供透明度的能力。因此,数据提供者可以看到数据扰动之后的隐私水平
- composition(可组合性)
ε1—DP和ε2—DP应用在相同或重叠的数据集上,结果满足(ε1+ε2)—DP。DP算法越多,隐私损失越大。
DP算法可以分为:基本算法和派生算法——差分隐私本身包含基本算法,派生算法是从现有方法中应用可组合性和后处理不变形推导出来的。
2.6 Deep Learning Using Convolutional Neural Networks
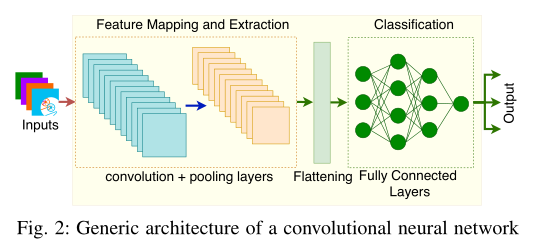
CNN通常被训练识别图像的基本特征。如上图所示,卷积层堆栈之后是一个池的中见功能,用来减少上一层的维度到下一维度。从最后一个卷积层产生的最终池输出产生一个相当大的1维向量,然后利用这些输入向量全连接人工神经网络(ANN),对输入图像进行预测(分类)。
当训练精度明显高于测试精度时,会发生过拟合。正则化、图像增强和超参数调整用来防止过拟合。
(1)正则化是对学习算法进行改变来减少泛化误差,正则化可以通过dropout实现,,即在每个训练周期中随机一定百分比的神经元,来避免过度拟合。
(2)图像增强是一种数据准备技术,对输入的图像使用不同的转化方法,例如反射,透明和旋转进行操作来产生很多更改的版本。
(3)dropout百分比、批处理大小、激活函数,神经元数、epoch数和优化器在不同训练阶段进行更改以产生更好的结果。
批处理大小是在一次向前/向后传播中的训练示例数。
激活函数定义特定神经元的输出,给定一组输入,有相应的权重,将非线性属性引入网络。
神经元是人工神经网络中的主要组成部分。
通过神经元向前/向后传递整个数据集的单程称为epoch
优化器被用来更新模型参数,例如权重和偏差值。
2.7 Amalgamation of SDN and NFV in Edge-Cloud Interplay
SDN和NFV是两种可编程基础设施,用来提高网络的可用性。这两种技术都基于创建网络功能虚拟实例的概念,SDN虚拟控制方面,NFV虚拟化重要的网络功能,例如加密通道。SDN和NFV的融合可以在复杂性、效率和服务质量方面带来很多先进功能。SDN控制NFV可以引入一系列有利于边缘云的虚拟化,从而提高本地设备和云服务的安全性和通讯质量。
3.APPROACH:LATENT
这部分讨论差分隐私算法机制应用在深度学习的LATENT中。LATENT可以被分类为派生的差分隐私算法基于随机响应技术。在应用差分隐私机制时,LATENT使用了差分隐私的两种属性:后处理不变性和可组合性;在随机化过程中,LATENT使用正则化、图像增强、超参数调整来优化性能。
3.1 引入中间层(LATENT)将差分隐私注入到CNN架构
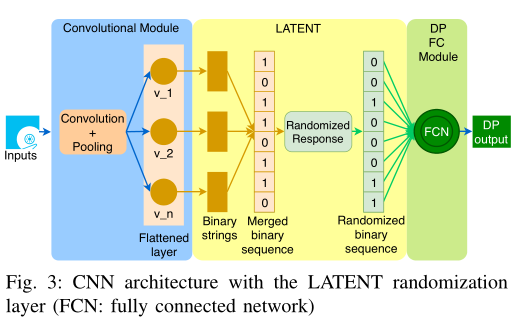
我们在卷积模块和FC模块之间插入了一个LATENT随机化模块。初始,使用卷积层和池层对输入特征进行降维处理,最终池层的输出是一个单一维数组。
(1)apply z-score normalization to LATENT’s input values
在随机化之前,LATENT将输入值转化为二进制值。输入值可能有不同范围。转化大值或小值为二进制可能设计大量的位。这可能对算法引入不同的复杂性。为了避免这种复杂性,我们对1维向量进行z—score标准化。
z-score 标准化
经过处理的数据符合标准正态分布,即均值为0,标准差为1。
其转化函数为:x* = (x - μ ) / σ, 其中μ为所有样本数据的均值,σ为所有样本数据的标准差。
z-score标准化方法适用于属性A的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。该种标准化方式要求原始数据的分布可以近似为高斯分布,否则效果会变得很糟糕。
标准化的公式很简单,步骤如下:
1.求出各变量(指标)的算术平均值(数学期望)xi和标准差si ;
2.进行标准化处理:
zij=(xij-xi)/si
其中:zij为标准化后的变量值;xij为实际变量值。
3.将逆指标前的正负号对调。
标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。
def z_score(x, axis):
x = np.array(x).astype(float)
xr = np.rollaxis(x, axis=axis)
xr -= np.mean(x, axis=axis)
xr /= np.std(x, axis=axis)
# print(x)
return x
(2)Define the bounds (lengths of the segments) for the binary conversion(定义二进制的界限)

特定的输入需对上界和下界进行初步估计。上图显示显示z-score标准化输入的二进制转换的位的排列。二进制字符串有三个主要段。第一位表示输入的符号(1表示负,0表示正),另两位分别是整数部分和小数部分。选择整数位取决于整数的最大值,由于z-score标准化,表示整数所需的比特位很小;表示小数位的比特数取决于精度,为了获取更高的精度,小数部分需要使用更多的位。
(3)Convert each value of the flattened layer to binary using the bounds
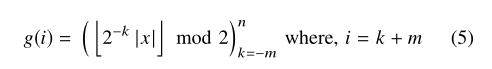
图4显示了整数/浮点数与二进制的直接映射。二进制表示可以根据图5生成,n代表整数部分的二进制位数,m代表小数部分的二进制位数,x为原始输入,g(i)表示二进制字符串的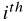 位,当k=-m时,表示最低有效位。
位,当k=-m时,表示最低有效位。
(4)Merge the binary strings to reduce the privacy loss(合并二进制字符串以减少隐私损失)
如果我们对r个二进制字符串分别进行随机化,将会产生r*ε隐私损失。
LATENT对合并的二进制进行随机化,隐私损失为输入值ε。
(5)Define the probability of randomization (p) in terms of ε
在随机响应中,相邻输入的差为d,则灵敏度为d。
在LATENT中,二进制字符串的长度L=(n+m+1),因此合并后的二进制字符串长度为l*r,r为卷积层输出的数目。
两个连续输入的差别最多为l×r,因此,灵敏度为l×r,随机化概率为:
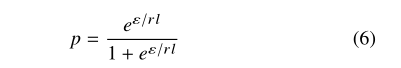
(6)Modifying optimized unary encoding to improve utility(修改优化一元编码来提高效用)
 可能会引入不可靠的随机化,我们使用优化一元编码(OUE),OUE分别扰动0和1来减少扰动0到1 (p0→1)的概率,因为输入二进制字符串很长时,需要0比1多。我们提出了一个新的方法。
可能会引入不可靠的随机化,我们使用优化一元编码(OUE),OUE分别扰动0和1来减少扰动0到1 (p0→1)的概率,因为输入二进制字符串很长时,需要0比1多。我们提出了一个新的方法。
-
UE
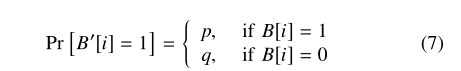
UE满足ε-LDP:
 sensitivity = 2
sensitivity = 2 -
OUE
OUE满足ε-LDP:
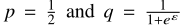 sensitivity = 2
sensitivity = 2
我们提出了新的方法:
- 在UB机制中加入了系数(α, the privacy budget coefficient)

- Modified OUE (MOUE)


(7)Improving the utility of randomized binary strings

(8)Conduct UER on the bits of the merged binary strings
(9)Generate a differentially private classification model using the FC module
3.2 Algorithm for Generating a Differentially Private CNN

7.8步骤不是很懂
3.3 The LDP Settings for LATENT
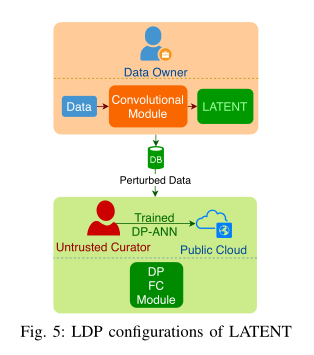
3.4 Integrating LATENT in the Amalgamation of SDN and NFV in Edge-Cloud Interplay