[ZJOI2006]碗的叠放（枚举）

Description

小H有n个碗需要放进橱柜，她希望将他们叠起来放置。你知道每个碗都是规则的圆柱体，并且都是上宽下窄，你已经测量出了每个碗的两个半径及高，请你帮小H找出一种叠放顺序，使得叠放出来的碗堆的高度尽量小，比如：

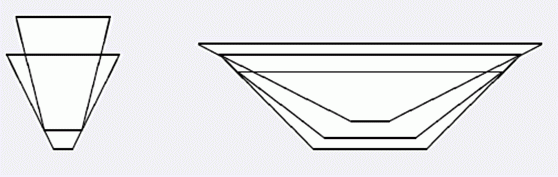
Input

第一行一个整数n，表示碗的数目。以下n行，每行三个整数h，r1，r2。分别表示碗高及两个半径。

Output

仅一个数，表示最小的高度。答案四舍五入取整。

Sample Input

3
50 30 80
35 25 70
40 10 90

Sample Output

55

HINT

数据范围：100%数据满足n < = 9。所有输入的数绝对值不超过1000。

n<=9，直接想一下暴力枚举每一种放置顺序，求最小的答案即可。

那我们怎么求一种排序方案的高度呢？

分几种情况讨论：

最简单的两种：

1.如果上面的碗的碗底半径比下面的碗的碗口半径还要大（或者等于），直接卡住。

2.如果上面的碗的碗口半径比下面的碗的碗口半径还要小（或等于），可以放进去，但有可能在下底面卡住。

如果这两种情况都不是，那只能看一下碗壁的斜率了。

1.下面的碗壁大于上面的碗壁的斜率

算出在哪里是卡住的，再加上即可。

2.下面的碗壁小于等于上面的碗壁的斜率

同理。

但是有一个小情况：有可能放完碗后中间是凹下去的，这时要取得是外面的碗高。

#include<bits/stdc++.h>
using namespace std;
struct data
{
	double a,b,c,d;
}a[21],b[21];
int n,c[21];
double x,y,z;
data putin(double a,double b,double c,double d)
{
	data aa;
	aa.a=a;
	aa.b=b;
	aa.c=c;
	aa.d=d;
	return aa;
}
double getxl(data a)
{
	return (a.d-a.b)/(a.c-a.a);
}
double work(data a,data b)//两个碗放置的高度 
{
	double p=a.b;
	if(b.a>=a.c)
	{
		return a.d;
	}
	a.b=0;
	a.d-=p;
	if(getxl(a)>getxl(b))
	{
		if(b.c>=a.c)
		{
			double k=a.d-(a.c-b.a)*getxl(b);
			return p+max(k,0.0);
		}
		double k=a.d-b.d-(a.c-b.c)*getxl(a);
		return p+max(k,0.0);
	}else{
		if(a.a>b.a)
		{
			return p;
		}
		double k=a.d-(a.c-b.a)*getxl(a);
		return p+max(k,0.0);
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lf%lf%lf",&x,&y,&z);
		a[i]=putin(y,0.0,z,x);
	}
	for(int i=1;i<=n;i++)
	{
		c[i]=i;
	}
	double minn=1e9;
	while(1)//计算每种排列的总高度 
	{
		b[0]=putin(1e9,0.0,1e9,0.0);
		for(int i=1;i<=n;i++)
		{
			double maxn=0;
			for(int j=0;j<i;j++)
			{
				maxn=max(maxn,work(b[j],a[c[i]]));
			}
			b[i]=putin(a[c[i]].a,a[c[i]].b+maxn,a[c[i]].c,a[c[i]].d+maxn);//放好的碗 
		}
		double maxn=0;
		for(int i=1;i<=n;i++)
		{
			maxn=max(maxn,b[i].d);
		}
		minn=min(minn,maxn);
		if(!next_permutation(c+1,c+n+1))//下一种排列 
		{
			break;
		} 
	}
	printf("%.0lf\n",minn);
	return 0;
}