Quoit Design (HDU 1007)平面的最近点对
题目大意：
给定平面上的 n 个点，求距离最近的两个点的距离的一半。 n <= 10^5.
晕乎乎的度过了一上午。。。
总之来学习下分治吧233
分治就是把大问题拆成小问题，然后根据对小问题处理出的结果合并成大问题的答案
比如说这道题，如果我们按照X坐标把所有的点分成两组：
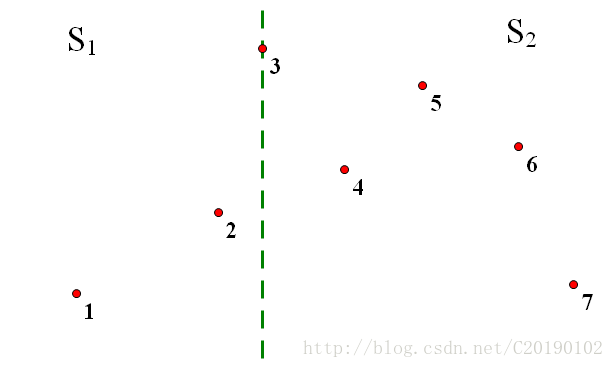
（木哈哈请叫我盗图狂魔○( ＾皿＾)っHiahiahia…
像上面我们把点分成了集合S1，S2
点对对应的被划分成3种：S1内，S2内，跨S1.S2
那假若我们分别处理出了S1，S2内的答案，再取个min叫做d
那么跨过分界线的点对就不能超过d，这是一个很有用的条件！不信？我们来看看
我们管分界线的X坐标叫x0
首先要知道，所有距离x0超过d的点都不用考虑
其次，这些点之间y的相对距离超过d的也不用考虑
这就把对一个点而言需要考虑的另一个点们限制在了一个小矩形里
再加上d是我们左右分治出来的答案
结论就是对于一个点我们最多只需要考虑6个点就可以了
你可以自己画画？这六个点都分布在矩形的顶点上
而具体实现其实就简单暴力了
具体就看码吧~
1 #include<cmath> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 int n,cnt; 6 struct point{ 7 double x,y; 8 }p[100005]; 9 int mk[100005]; 10 bool cmpx(point A,point B){return A.x<B.x;} 11 bool cmpy(int A,int B){return p[A].y<p[B].y;} 12 double dis(int x,int y){return sqrt((p[x].x-p[y].x)*(p[x].x-p[y].x)+(p[x].y-p[y].y)*(p[x].y-p[y].y));} 13 double solve(int l,int r){ 14 if(l==r)return 1e18; 15 if(l+1==r)return dis(l,r); 16 int mid=(l+r)>>1; 17 double x0=(p[mid].x+p[mid+1].x)/2.0; 18 double d=min(solve(l,mid),solve(mid+1,r)); 19 cnt=0; 20 for(int i=l;i<=r;i++) 21 if(p[i].x-x0<=d&&p[i].x-x0>=-d) 22 mk[++cnt]=i; 23 sort(mk+1,mk+1+cnt,cmpy); 24 for(int i=1;i<=cnt;i++) 25 for(int j=i-1;j>=1;j--) 26 if(p[mk[i]].y-p[mk[j]].y>d)break; 27 else d=min(d,dis(mk[i],mk[j])); 28 return d; 29 } 30 int main(){ 31 scanf("%d",&n); 32 for(int i=1;i<=n;i++)scanf("%lf%lf",&p[i].x,&p[i].y); 33 sort(p+1,p+1+n,cmpx); 34 printf("%.4lf",solve(1,n)); 35 return 0; 36 }
