20172325 2018-2019-2 《Java程序设计》第六周学习总结
20172325 2018-2019-2 《Java程序设计》第六周学习总结
教材学习内容总结
本周学习第十章——树
1.什么是树
(1)树是一种数据结构,与之前学过的栈、队列和列表这些线性数据结构不同,树是一种非线性数据结构,其元素被组织成了一个层次结构。
(2)树由一个包含结点和边的集合构成,“结点”就像“果实”,“边”就像“树枝”,其中的元素被储存在这些结点中,边则将一个结点和拎一个结点连接起来。一棵树只有一个根,根就是那个位于该树顶层的唯一结点。
(3)树的相关术语
- 结点的子树的根称为结点的孩子,相应的,该结点称为孩子的双亲;
- 同一个双亲的孩子之间互称兄弟;
- 结点的祖先是从根到该结点所经分支上的所有结点。;
- 以某结点为根的子树中的任意结点都称为该结点的子孙;
- 结点的层也就是从根结点到该结点的路径长度;
- 树的高度指从根到叶子之间最远路径的长度。
(4)树的图解
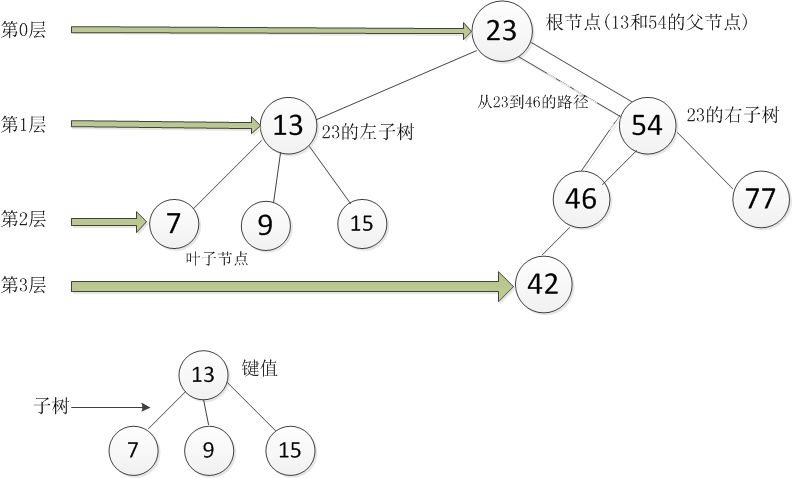
树的图解就和高中生物中的遗传示意图类似,可以帮助理解。
2.树的分类
(1)最重要的标准是树中任一结点可以具有的最大孩子数目,这个值称为该树的度。在这种分类标准下,将每一结点限制为不超过n个孩子的树称为一棵n元树,对结点所含有的孩子数目无限制的数称为广义树。
n元树特别重要。结点最多具有两个孩子的树称为二叉树,这种树在大多数情况下有用。
(2)按照该树是否平衡分为平衡树与非平衡树。平衡的粗略定义:树的所有叶子是否都位于同一层或者彼此之间是否相差不超过一个层,是则为平衡,否则为非平衡。
(3)完全树:如果某数是平衡的,且底层所有的叶子都位于左边,则认为该树是完全的。
(4)满树:如果一棵n元树的所有叶子都位于同一层且每一结点要么是一片叶子要么正好具有n个孩子,则称树是满的。
3.实现树的策略
- 计算策略:对某些特定类型的树,特别是二叉树而言,二叉树的存储设从0开始,左子树为(2n+1),右子树为(2n+2).。但是该实现方法存在缺陷,它会给不包含数据的树位置分配空间,这就浪费了大量的储存空间。
- 模拟链接策略:每一个结点存储的将是每一个孩子(可能还有双亲)的数组索引,而不是指向其孩子(可能还有双亲)的指针对象的引用变量,但是该方式增加了删除树中元素的成本。
- 树的分析:树是实现其他集合的有用而且高效的方式,一般而言,一棵含有m个元素的平衡n元树具有的高度为log n(m),随着n的增加,树的效率就会越发引人入目。
4.树的遍历
遍历四棵树有四种基本方法:

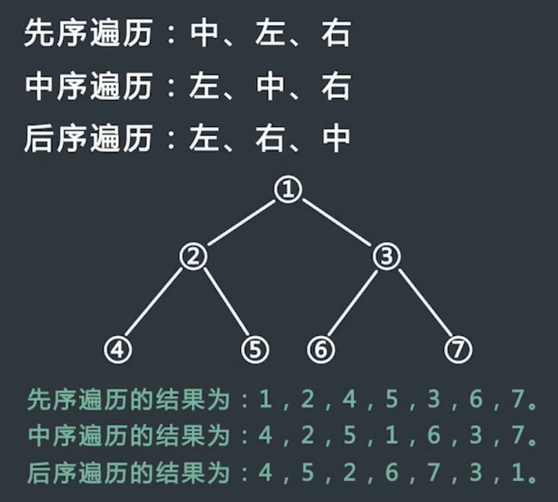
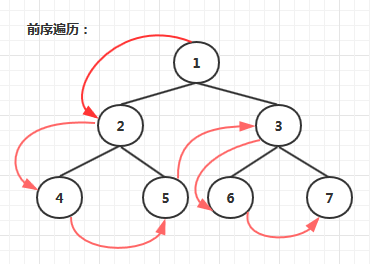
前序遍历:从根结点开始访问每一结点极其孩子。
Visit node
Traverse(left child)
Traverse(right child)
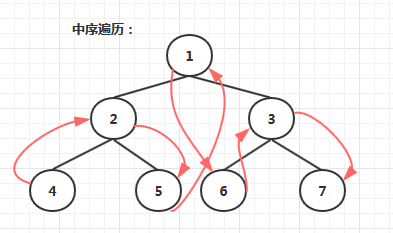
中序遍历:从根节点开始,访问结点的左孩子,然后是该结点,再然后是任何剩余结点。
Traverse(left child)
Visit node
Traverse(right child)
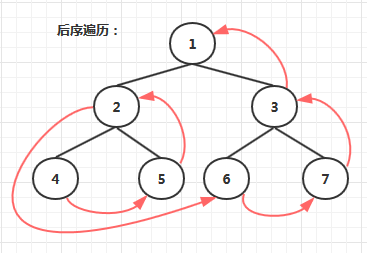
后序遍历:从根结点开始,访问结点的孩子,然后是该结点。
Traverse(left child)
Traverse(right child)
Visit node
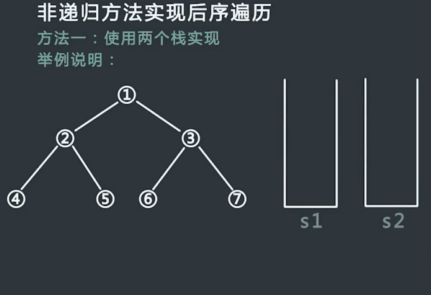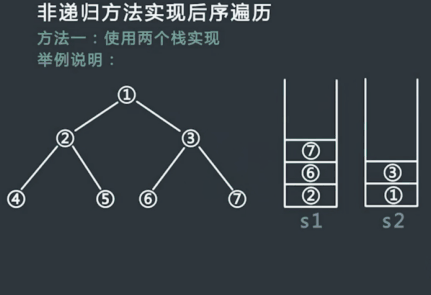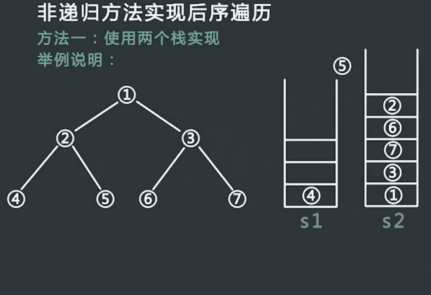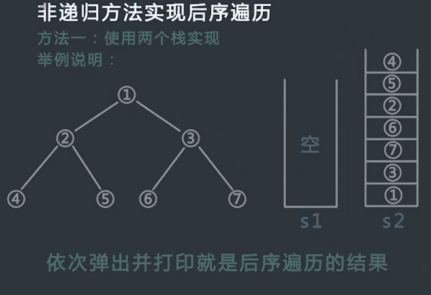
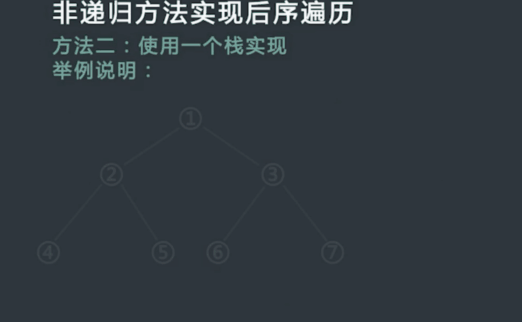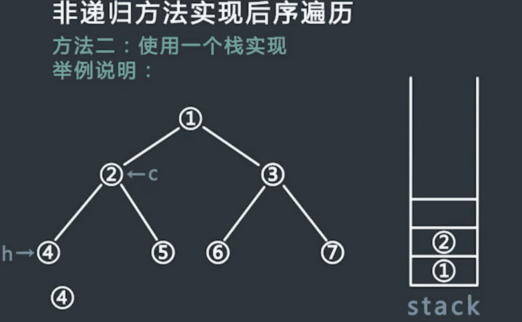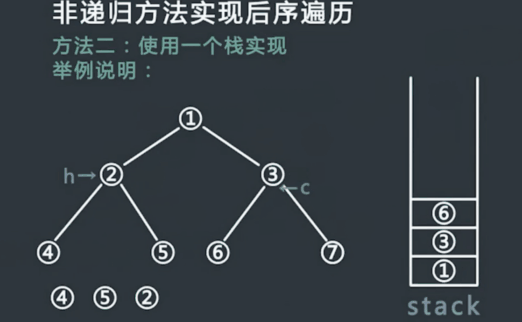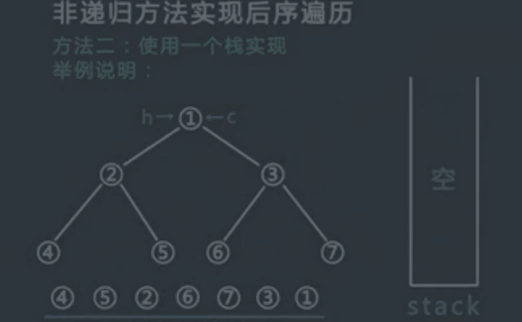
层序遍历:从根结点开始,访问每一层的所有结点,一层一层。
Create a queue called nodes
Create an unordered list called results
Enqueue the root onto the nodes queue
While the nodes queue is not empty
{
Dequeue the first element from the nodes queue
If that element is not null
Add that element to the rear of the results list
Enqueue the children of the element on the nodes queue
Else
Add null on the result list
}
Return an iterator for the result list
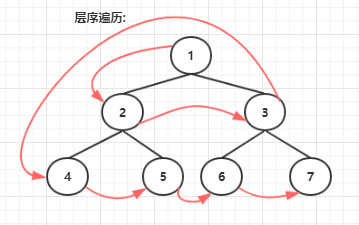
二叉树
1.二叉树的定义
二叉树是n(n≥0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
2.二叉树的特点
(1)每个结点最多有两颗子树,所以二叉树中不存在大于2的结点。注意是最多有2棵子树。没有子树或者有一颗子树都是可以的。
(2)左子树和右子树是有顺序的,次序不能颠倒。就像左右手。
(3)即使树中某结点只有一棵子树,也要区分是左子树还是右子树。
3.二叉树具有五种基本形态:
- 空二叉树
- 只有一个根节点
- 根节点只有左子树
- 根节点只有右子树
- 根节点既有左子树又有右子树
4.二叉树的基本性质
-
性质1:在二叉树的第i层上至多有2^(i - 1)个结点(i ≥ 1)
-
性质2:深度为k的二叉树至多有2^k - 1个结点(k ≥ 1) 。这里要和看清楚,是2^k后再减去1。
-
性质3:对任何一个二叉树,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
-
性质4:具有n个结点的完全二叉树的深度为[log2n] + 1( [x]表示不大于x的最大整数 )。
-
性质5:如果对一棵有n个结点的完全二叉树(其深度为[log2n] + 1)的结点按层序编号(从第i层到第[log2n] + 1层,每层从左到右),对任一结点i(1 ≤ i ≤ n)有:
(1)如果i = 1,则结点i是二叉树的根,无双亲; 如果i > 1,则其双亲结点是 [i / 2]。
(2)如果2i > n,则结点i无左孩子(结点i为叶子节点);否则其左孩子是结点2i
(3)如果2i + 1 > n,则结点无右孩子;否则其右孩子是结点2i + 1。
教材学习中的问题和解决过程
-
问题1:在学习第二种树的分类的时候,对于平衡的定义模糊搞不清楚,尤其是对课本上仅有的一个示例图一知半解。
-
问题1解决方案:查阅了多种平衡以及不平衡树的例子,在总结中发现了规律。对于平衡树的理解关键点在于“所有叶子处于同一层或者彼此相差不超过一层”,其中所有和彼此是关键,判断时需要考虑到所有的叶子,彼此指的是所有叶子两两之间。下面给出多种自己判断核对过得平衡树与非平衡树。
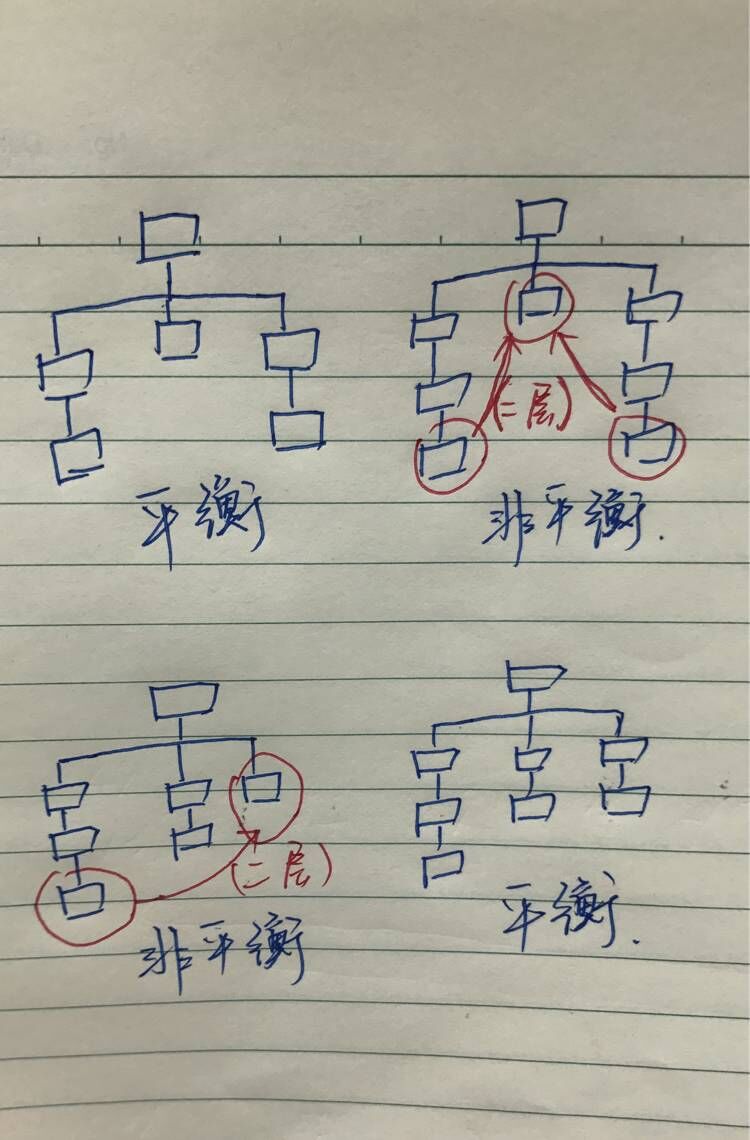
-
问题2:如果是有三个结点的树,有几种形态?如果是有三个结点的二叉树,又有几种形态?
-
问题2解决方案:
1.如果是无序的数,只有两种,一种是一个根节点,下面2个子树。
2.另一种是一个根节点有一个子树,这个子树还有一个子树。 -
问题3:在判断完全二叉树的时候不熟练
-
问题3解决方案:查找资料,总结了一部分完全二叉树的特点。

-
问题4:上课时王老师说孩子兄弟表示法很重要,但是不太明白具体的意思和理解,尤其是觉得如果一个结点有三个孩子,那么除了结点和第二个孩子,第三个孩子如何查找?
-
问题4解决方案:任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此节点的右兄弟。 这种表示法,给查找某个结点的孩子带来了方便,只需要通过firstchild找到此节点的长子,然后通过长子结点的rightsib找到它的二弟,接着一直下去,直到找到具体的孩子。
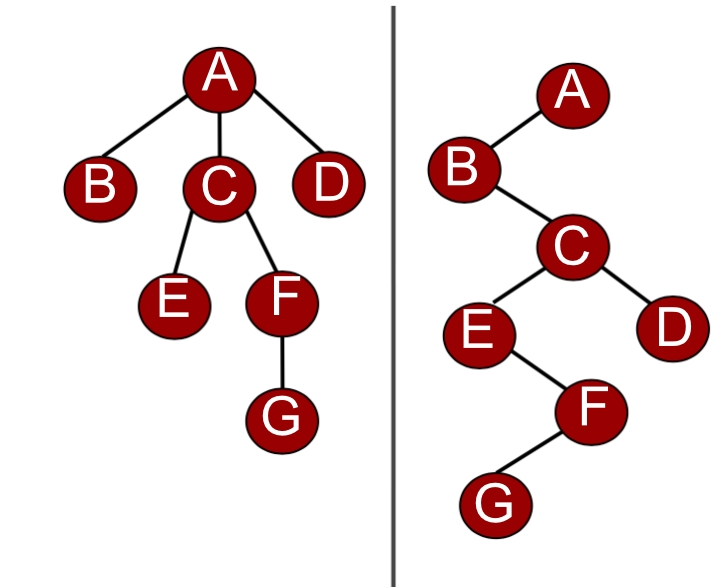
当然如果想要找某个结点的双亲,这个表示法也是有缺陷的,那么怎么办呢?如果真的有必要,完全可以再增加一个parent指针域来解决快速查找双亲的问题。其实这个表示法的最大好处就是把它一棵复杂的树变成了一棵二叉树,这样就可以充分利用二叉树的特性和算法来处理这棵树了。
代码调试中的问题和解决过程
-
问题1:运行PostfixTester时,没有出现应该出现的树和数字。
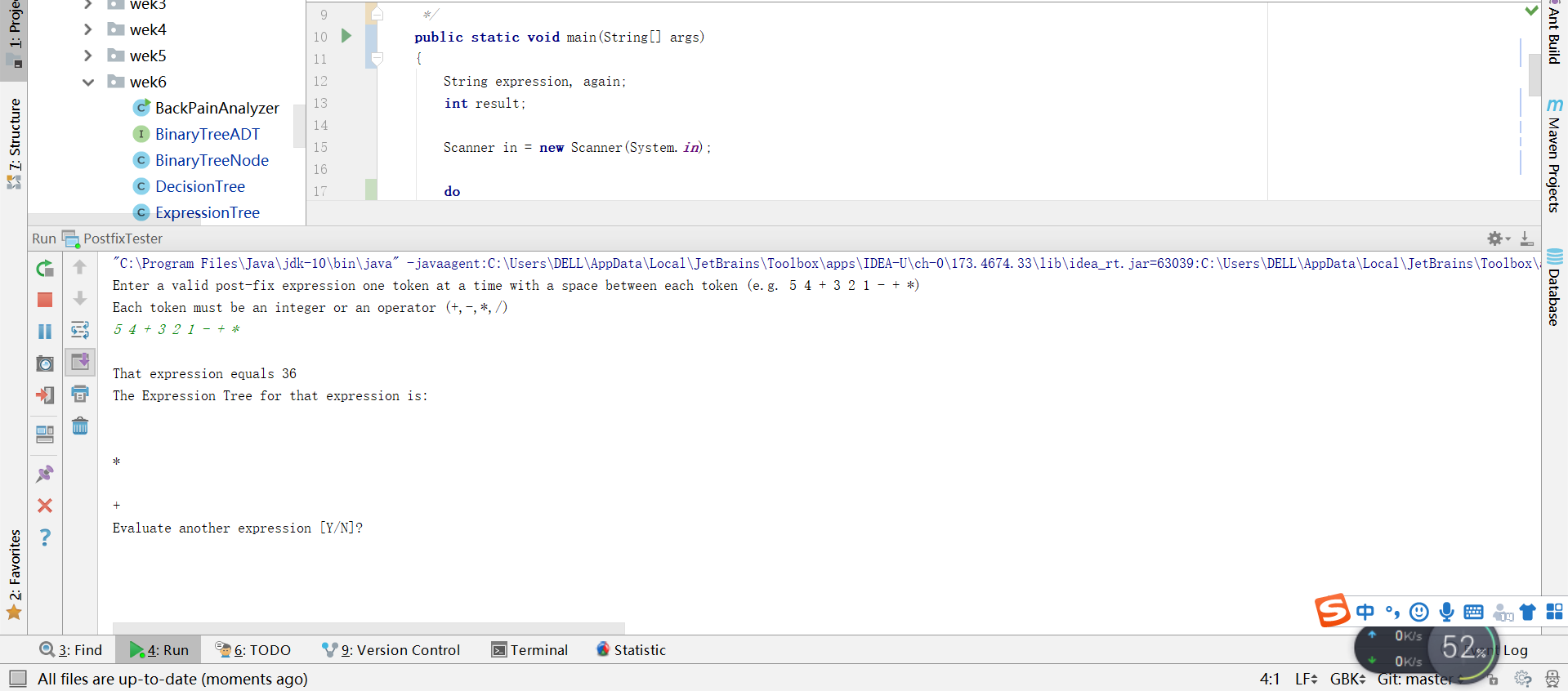
-
问题1解决方案:LinkedBinaryTree.java文件中的方法发生了错误,于是进行了调试,之后发现GetRight和GetLeft的返回值是错误的,是没有编写成功height()方法。
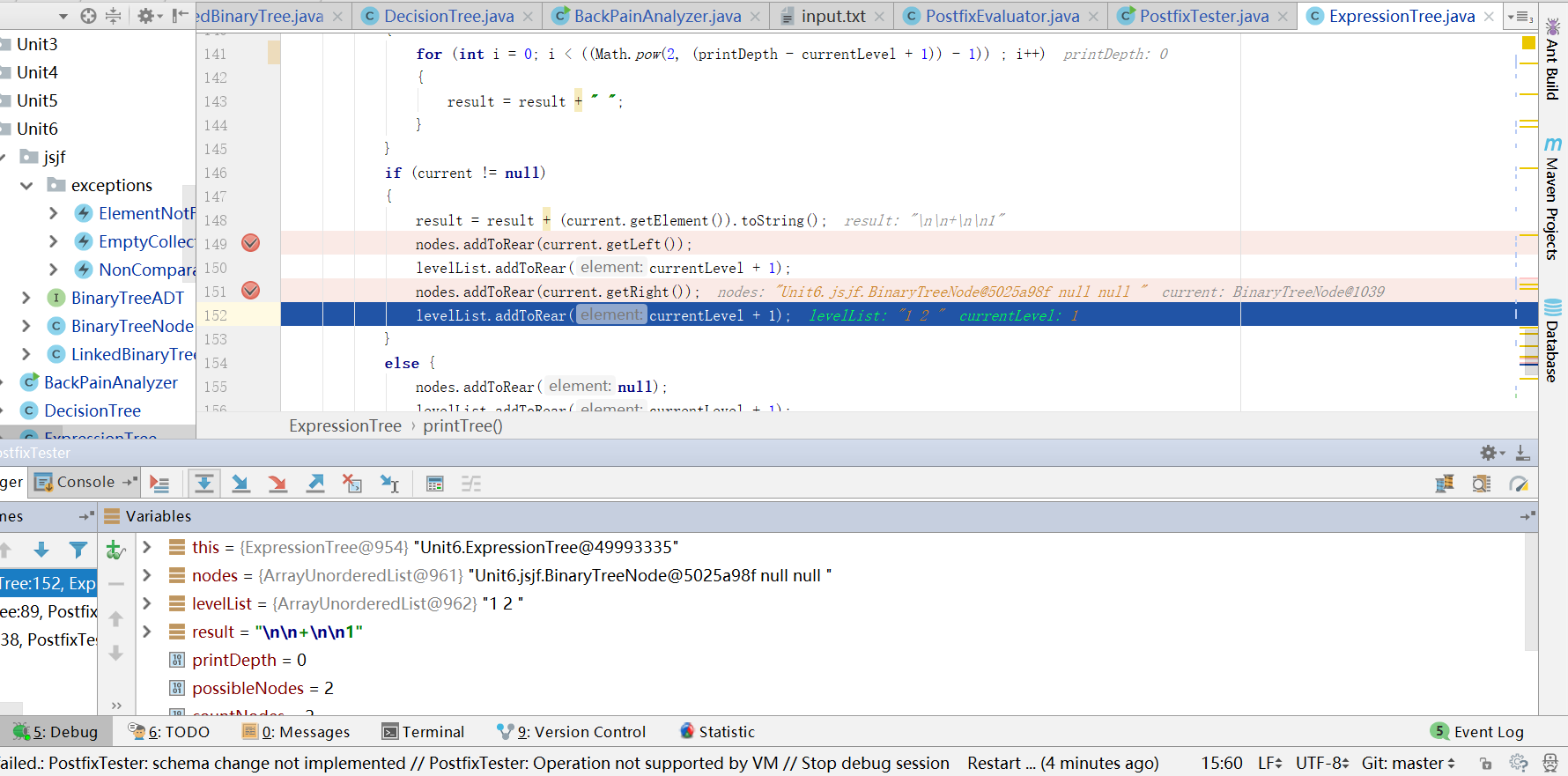

代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
上周未测试
结对及互评
点评过的同学博客和代码
- 本周结对学习情况
- 20172306
- 结对学习内容
- 第十章内容
- 第十章代码问题
其他(感悟、思考等,可选)
有时候人是需要压力和教训的,在经历上次没有安排好时间的问题之后,通过自己的调整,学习任务一步一步向着高质量的方向完成,本周对第十章的掌握程度自己觉得比上一次又有了些许进步,果真进步都是在困难中历练出来的,迎难而上,继续加油。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 20/20 | |
| 第二周 | 941/8481 | 1/2 | 18/20 | |
| 第三周 | 653/9134 | 1/3 | 22/20 | |
| 第四周 | 1728/4385 | 2/5 | 8/28 | |
| 第五周 | 933/5318 | 1/6 | 18/20 | |
| 第六周 | 1082/5877 | 1/7 | 20/18 |




