20172325 2018-2019-1 蓝墨云班课实验--哈夫曼树的编码
20172325 2018-2019-1 蓝墨云班课实验--哈夫曼树的编码
一、测试要求
-
设有字符集:S={a,b,c,d,e,f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。
给定一个包含26个英文字母的文件,统计每个字符出现的概率,根据计算的概率构造一颗哈夫曼树。
并完成对英文文件的编码和解码。 -
要求:
(1)准备一个包含26个英文字母的英文文件(可以不包含标点符号等),统计各个字符的概率
(2)构造哈夫曼树
(3)对英文文件进行编码,输出一个编码后的文件
(4)对编码文件进行解码,输出一个解码后的文件
(5)撰写博客记录实验的设计和实现过程,并将源代码传到码云
(6)把实验结果截图上传到云班课
二、哈夫曼树编译步骤
哈夫曼编码是有贪心算法来构造的最优前缀码。哈夫曼编码是通过二叉树的形式构造表示的,其中构造出的二叉树一定是一颗满二叉树。
下面简述哈夫曼编码的构造过程:
1、由给定的m个权值{w(1),w(2),w(3),...,w(m)},构造m课由空二叉树扩充得到的扩充二叉树{T(1),T(2),....T(m)}。每个T(i)(1<= i <= m)只有一个外部节点(也是根节点),它的权值置为m(i)。概括一下就是把原先的节点封装成二叉树结点的形式。
2、在已经构造的所有扩充二叉树中,选取根结点的权值最小和次最小的两棵,将他们作为左右子树,构造成一棵新的扩充二叉树,它的根结点(新建立的内部结点)的权值置为其左、右子树根结点权值之和。
3、重复执行步骤(2),每次都使扩充二叉树的个数减少一,当只剩下一棵扩充二叉树时,它便是所要构造的哈夫曼树。
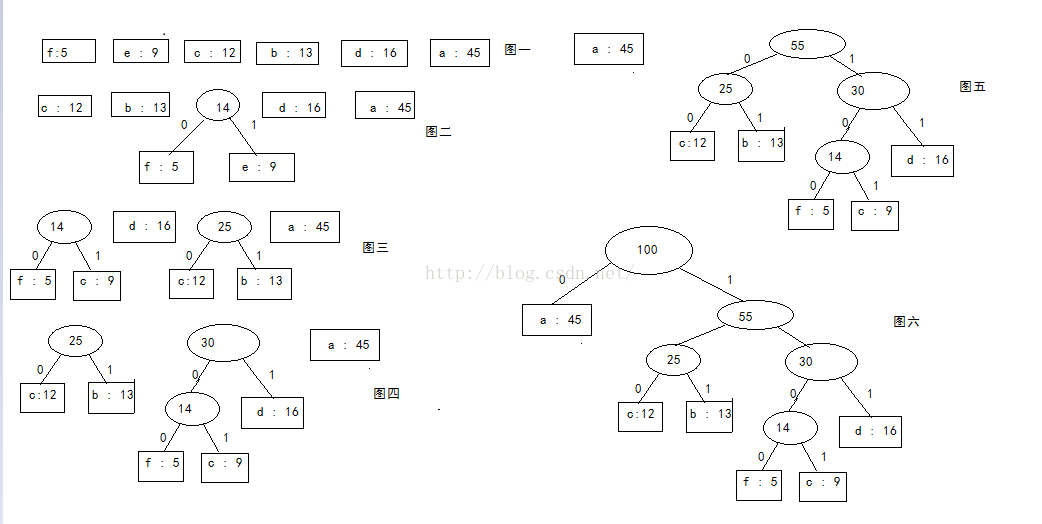
从图中可以看出,每次选择两个最小的结点,生成新的二叉树之后,新二叉树的根结点重新加入到原结点序列中。
三、测试过程
- 1.定义TreeNode节点
private static class TreeNode implements Comparable<TreeNode>{
TreeNode left;
TreeNode right;
int weight;
char ch;
String code;
public TreeNode(int weight,TreeNode left,TreeNode right) {
this.weight = weight;
this.left = left;
this.right = right;
this.code = "";
}
@Override
public int compareTo(TreeNode o) {
if (this.weight > o.weight) {
return 1;
}else if (this.weight < o.weight) {
return -1;
}else {
return 0;
}
}
}
ch保存相应字符。code保存0或1,方便打印字符编码。
2.实现核心算法
这里用了一个TreeSet的容器装节点,因为它自带排序功能。(前提是对象为Comparable的子类)
public static TreeNode huffman(TreeMap<Integer, Character> data) {
TreeSet<TreeNode> tNodes = new TreeSet<>();
Set<Integer> weights = data.keySet();
Iterator<Integer> iterator = weights.iterator();
while (iterator.hasNext()) {
int weight = iterator.next();
TreeNode tmp = new TreeNode(weight, null, null);
tmp.ch = data.get(weight);
tNodes.add(tmp);
}
while (tNodes.size() > 1) {
TreeNode leftNode = tNodes.pollFirst();
leftNode.code = "0";
TreeNode rightNode = tNodes.pollFirst();
rightNode.code = "1";
TreeNode newNode = new TreeNode(leftNode.weight+rightNode.weight,
leftNode, rightNode);
tNodes.add(newNode);
}
return tNodes.first();
}
3.得到字符编码
private static void code(TreeNode t) {
if (t.left != null) {
t.left.code = t.code + t.left.code;
code(t.left);
}
if (t.right != null) {
t.right.code = t.code + t.right.code;
code(t.right);
}
}
4.打印字符编码结果
public static void print(TreeNode root) {
if (root != null) {
if (root.left == null && root.right == null) {
System.out.println(root.ch + " 编码:" + root.code);
}else {
print(root.left);
print(root.right);
}
}
}
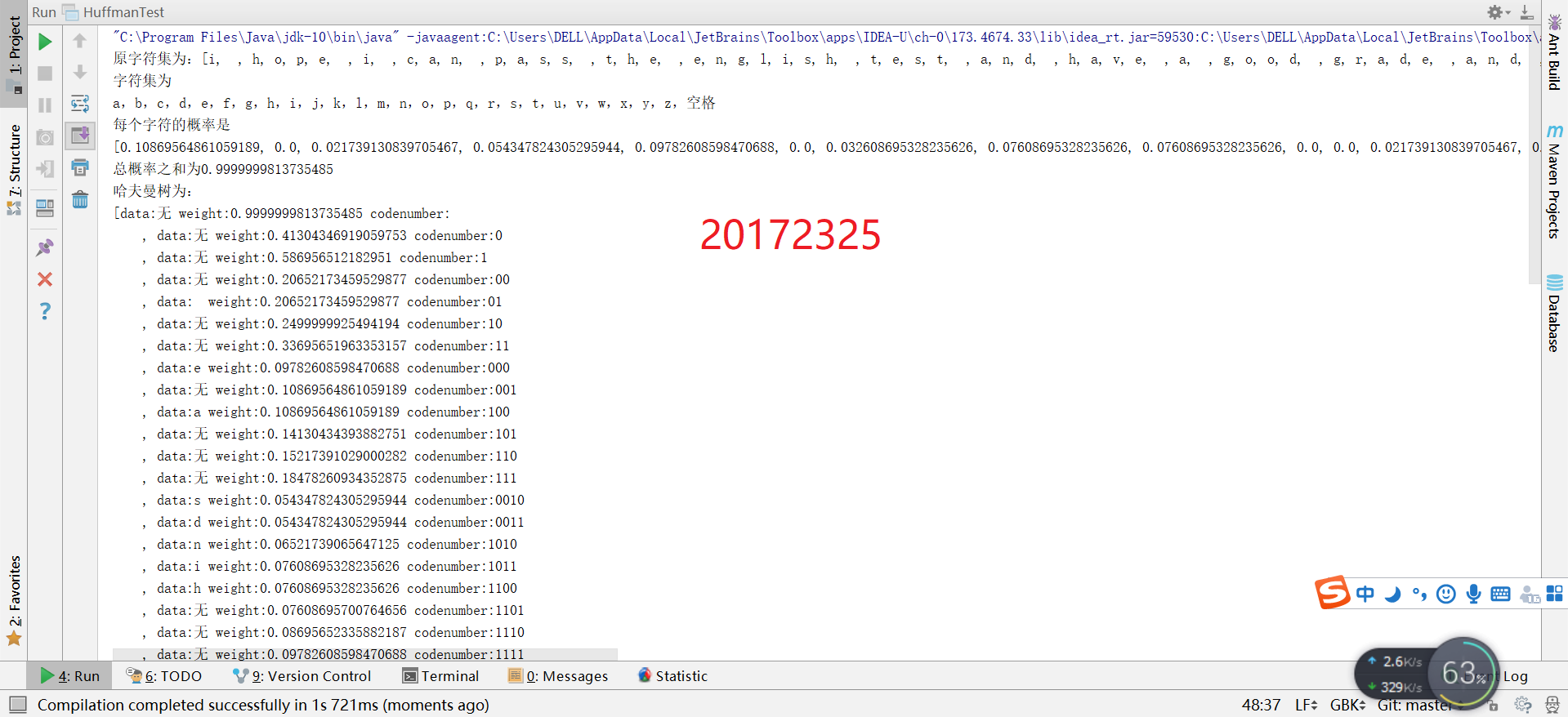
四、测试结果