数据结构 第六章 图 -- 基本概念
图:
实现数据的多对多的关系
分类: 有向图、 无向图
搜索: 广度优先搜索(BFS)、深度优先搜索(DFS)
表示: G=(V,E) V是顶点集 E 为边集
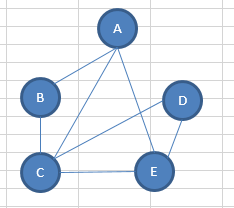
V = {A,B,C,E,D}
E = {(A B),(A C),(A E),(B C),(C D),(C E),(E D)}
V阶= |V| = 5
E阶=|E|=6 边的个数
struct E{
startPoint; // 开始顶点 弧尾
endPoint; // 结束顶点 弧头
}
flag; 0 -有向图 无向图
* 线性表 树都可以为空,但是图不能为空,没有空图的概念。
* 有向图 无向图

边全为有向边的图 称为 有向图,边全为无向边的图 为无向图
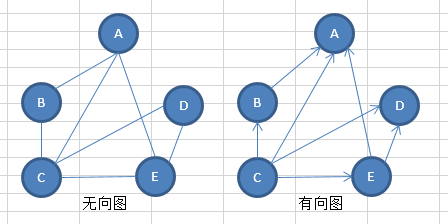
有向图的边集也称为 弧集 / 类似数学中的向量集
E = { <B,A>, <C,A>, <C,B>,<C,D>,<C,E>,<E,D>}
<B,A>称为 B邻接到A 或者 A邻接自A ----> 邻接矩阵法
简单图:
无重复边,不存在结点到自身的边

重复图:【仅作了解】
存在重复边,或存在结点到自身的边
完全图:边是满的图形
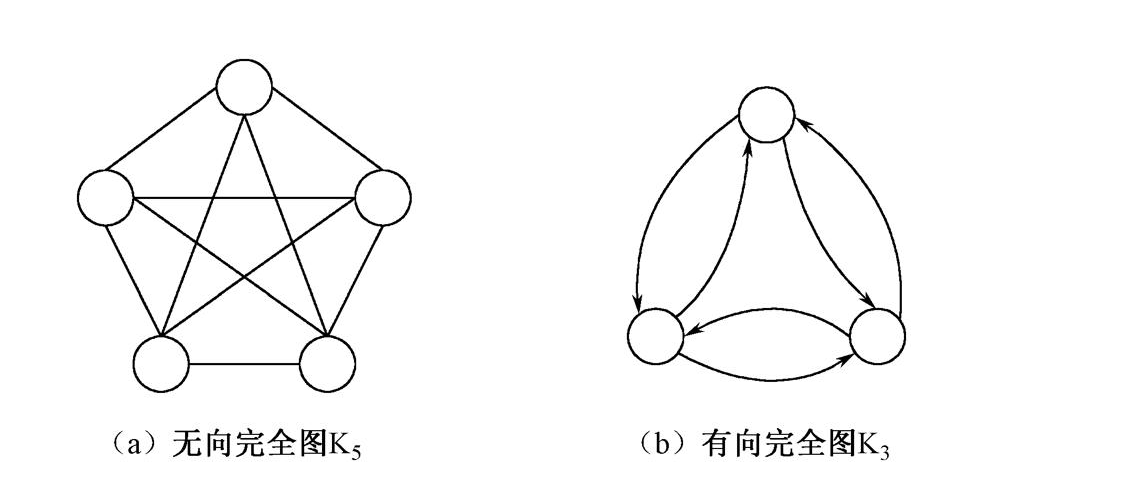
无向完全图n个顶点的边的个数:
n-1 + n-1+....+0 = n(n-1) / 2
有向完全图n个顶点边的个数:
n-1 +n-1 + ... + n-1 = n(n-1)
子图:图G = (V,E) 图G1=(V1,E1),其中 V1 包含于V && E1 包含于 E,则 G1是G的子图
G1是G的子图的前提下,V1=V,则G1是G的生成子图。

边集为空,顶点集不为空,也称为子图,如下图:
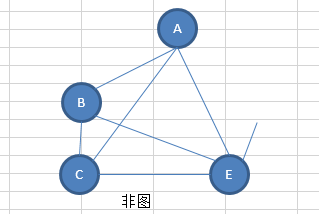
本身图形就不是一个图,那就更不是子图了,如下图,有一条边没有端点,不符合图的定义,则不能称之为子图。
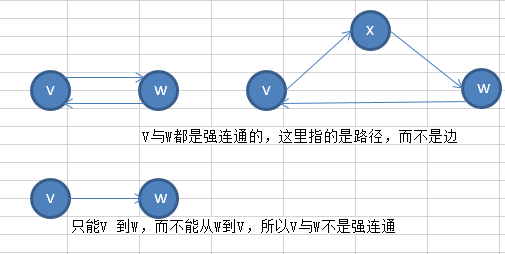
** 无向图的连通 与 有向图的强连通
无向图中,若从顶点V到顶点W有路径存在,则称 V与W是连通。如下图:

在有向图中,若从顶点V到顶点W && 顶点W到顶点V 都有路径存在,则称为V与W是强连通的
* 无向图-连通图:任意两个结点之间都是连通的。
*有向图-强连通图:任意两个结点之间都是强连通的。
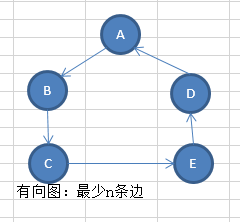
无向图的连通分量,也称为极大连通子图
定义:
对于图 G 的一个连通子图 GL1,如果不存在GL2 包含GL1(GL2是G的一个连通子图),则,GL1为G的连通分量【极大连通子图】
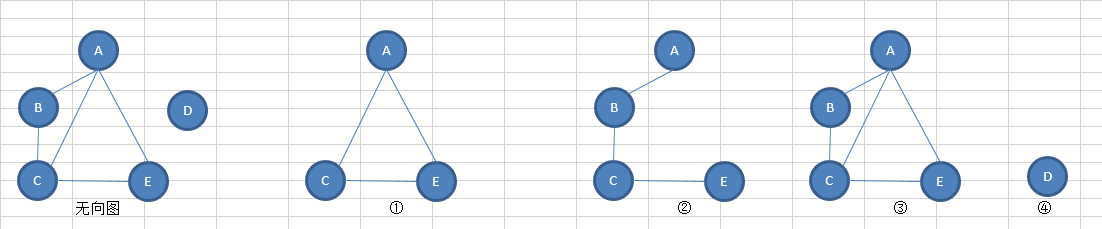
其中,③④为该无向图的连通分量
**有向图的 强连通分量,也称为极大强连通子图【多了一个字 强】
定义:
对于图 G 的一个强连通子图 GL1,如果不存在GL2 包含GL1(GL2是G的一个强连通子图),则,GL1为G的强连通分量【极大强连通子图】
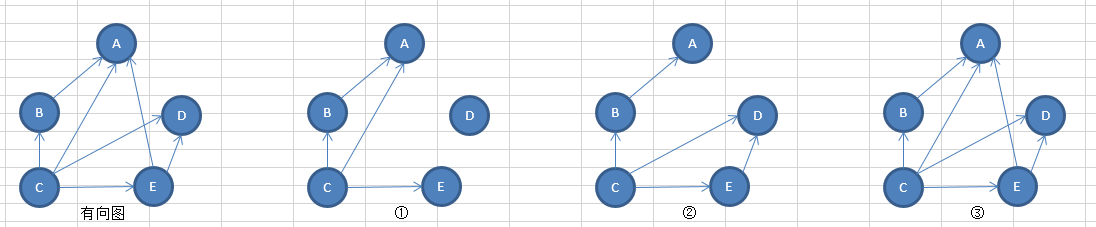
③为该有向图的强连通分量
【结论】
结论: 如果图为(强)连通图,那么他的(强)连通分量 是它自己本身,如果图是非(强)连通图,那么他的(强)连通分量 有多种情况。
【以下讨论的内容所对应的图为 无向图】
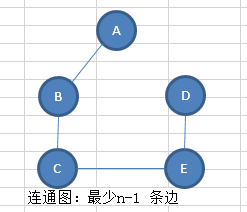
极小连通子图:连通子图包含所有顶点且包含的边最少。
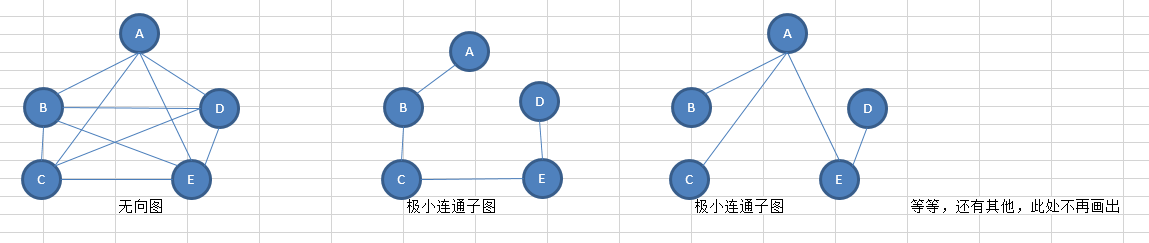
上面的极小连通子图也称为 生成树。
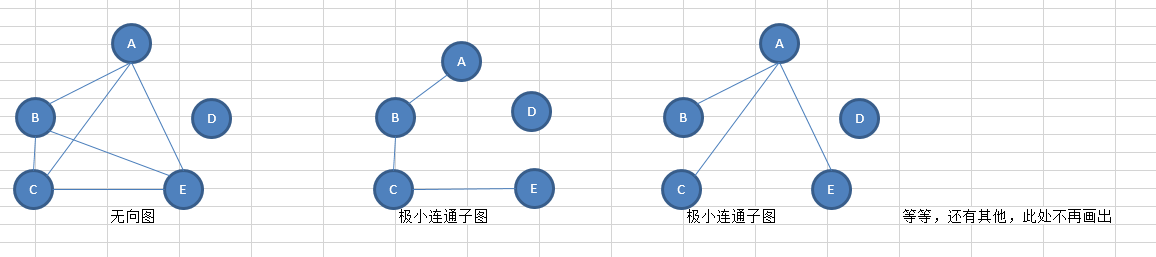
上面的极小连通子图也称为 生成森林。
【结论】
*** 生成树:只能由连通图生成
连通图包含全部顶点的一个极小连通子图
生成树只有图本身是生成树的情况下才唯一(就是其自己本身),其他情况则不唯一
有 n个顶点的图 的生成树则有 n-1 条边
***生成森林:只能由非连通图生成
非连通图的所有连通分量的 生成树 组成 生成森林;
解析:
非连通图 --> 连通分量 --> 生成树 --> 组成 --> 森林
* 顶点的度:
无向图中,顶点v的度为以v为端点的边的个数,记为 TD(v)。
* 有向图中,顶点v的度为出度OD(v)与入度ID(v)的和。
结束




