数据结构 第五章 树-应用-并查集与哈夫曼树
** 树的应用**
【树的并查集】
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
合并:合并两个集合
查找:判断两个元素是否在一个集合
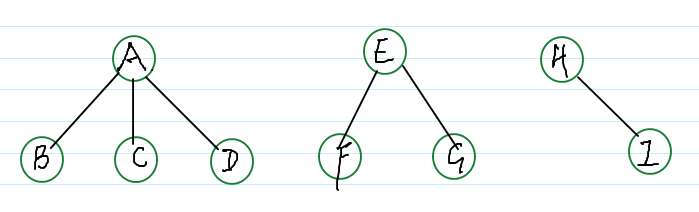
A E H 为根结点的三棵树:
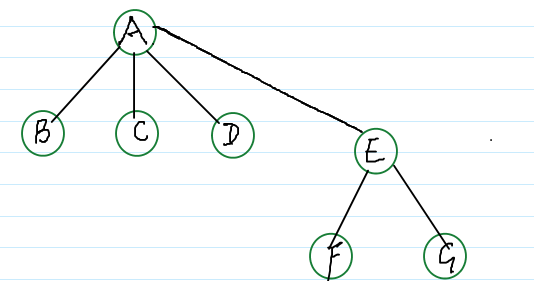
root(F) == E root(D) == A, 他们不是同一个根结点,所以可以对 D 所在的集合 与 F 所在的集合进行合并,如下:
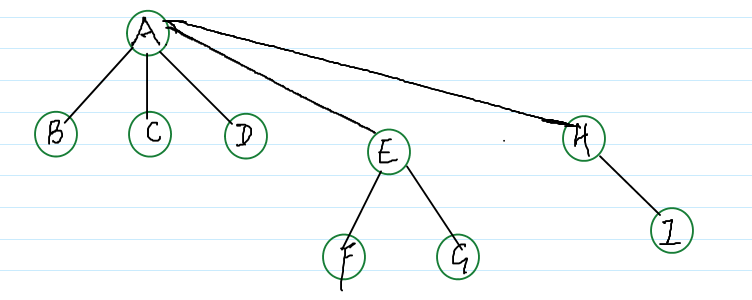
继续合并:
双亲表示法的并查集操作:
并查集的结构定义:
int UFSets[SIZE]; //集合元素数组(双亲指针数组)
Find操作(函数在并查集S中查询并返回包含元素x的树的根):
int Find(int S[],int x) {
while(S[x]>=0) //循环寻找x的根
x=S[x];
return x; //根的S[]小于0
}
Union操作(函数求两个不相交子集合的并集):
void Union(int S[],int Root1, int Root2) //Root1与Root2不同,表示子集合的名字
{
S[Root2]=Root1; //将根Root2连接到另一个根Root1下面
}
** 使用链式存储存储树**

不需要这么麻烦。
查找操作时,直接返回成员变量 root 结点。
合并操作时,直接将A树的root 结点作为 B树的根结点,B.root.father = A.root。
** 并查集的应用:图的最小生成树 -- 克鲁斯卡尔(Kruskal)算法。
【哈夫曼树】
树的带权路径长度(Weighted Path Length of Tree,简记为WPL)
结点的权:在一些应用中,赋予树中结点的一个有某种意义的实数。
结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积。
树的带权路径长度(Weighted Path Length of Tree):定义为树中所有叶结点的带权路径长度之和,通常记为:
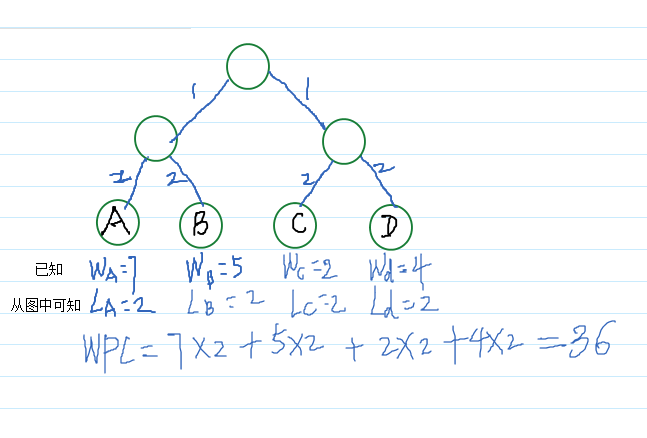
WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),n个权值Wi(i=1,2,...n)构成一棵有n个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)
如下图的带权树:
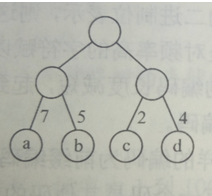
计算如下:
哈夫曼树:
定义: 给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
性质:
*初始的结点都会成为叶结点,双亲结点都是新生成的结点。
*权值越大的结点离根结点越近,反之,权值越小的结点离根结点越远。
*哈夫曼树中没有度为1的结点,要么是度为0的叶结点、要么是度为2的双亲结点。
*n个叶子结点的哈夫曼树的结点总度数为 2n - 1,度为2的结点为 n-1
哈夫曼树构造:

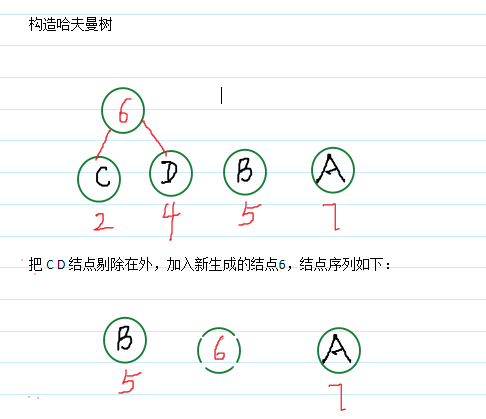
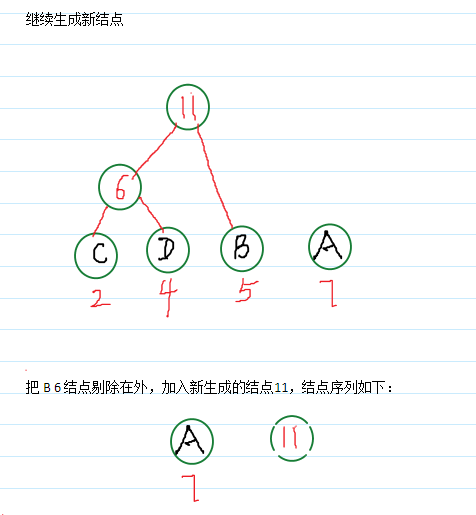
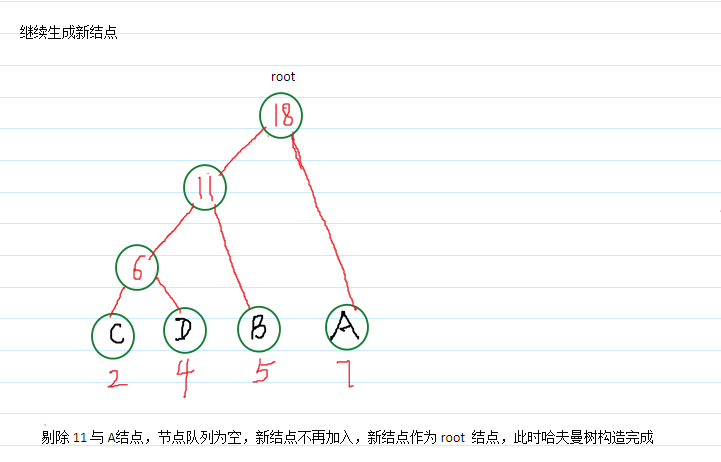
*哈夫曼树结点结构:

哈夫曼树及前缀码生成的 流程图:
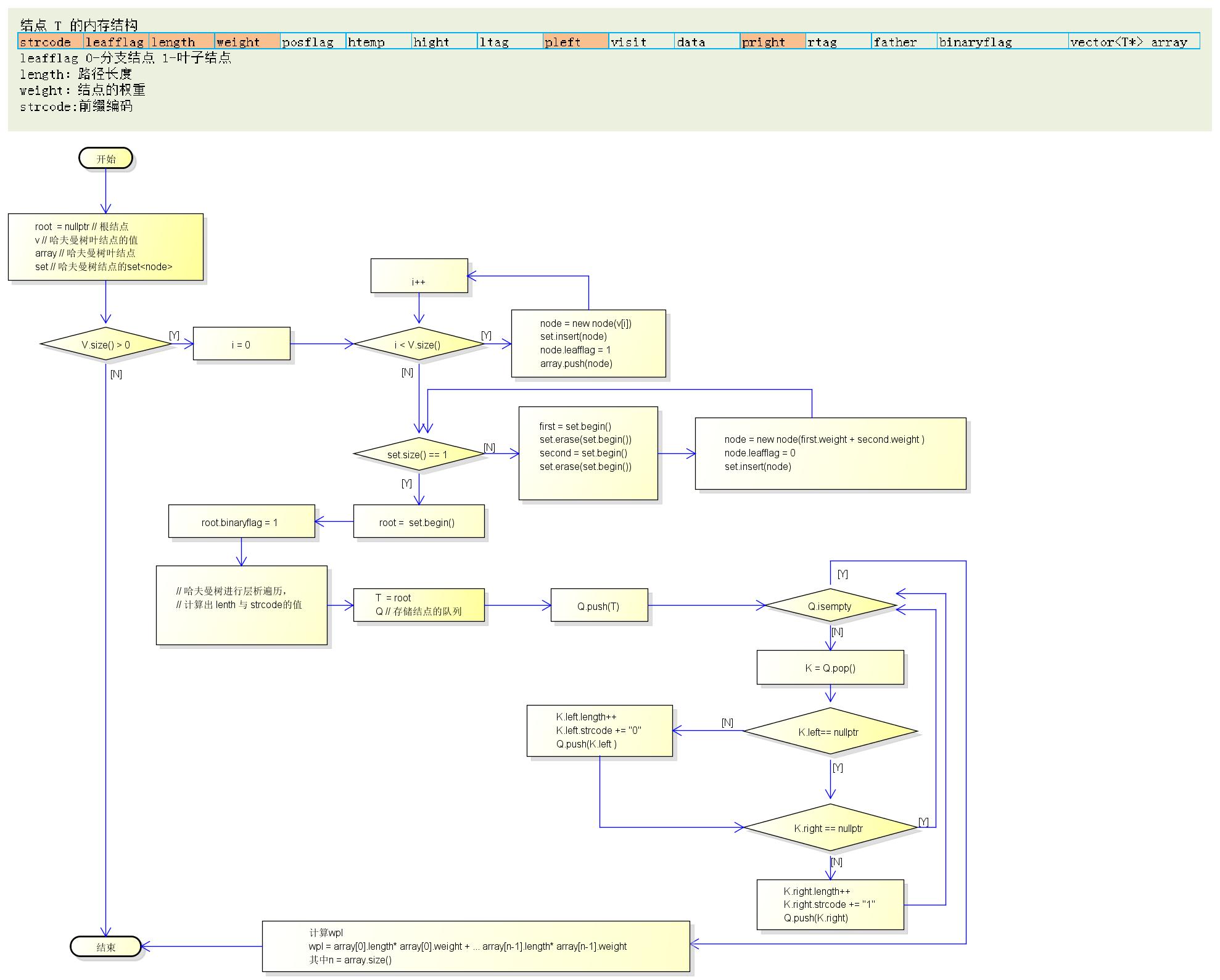
*应用: 编码压缩,在数据传输中使用:
在处理字符串序列时,如果对每个字符串采用相同的二进制位来表示,则称这种编码方式为定长编码。若允许对不同的字符采用不等长的二进制位进行表示,那么这种方式称为可变长编码。可变长编码其特点是对使用频率高的字符采用短编码,而对使用频率低的字符则采用长编码的方式。这样我们就可以减少数据的存储空间,从而起到压缩数据的效果。而通过哈夫曼树形成的哈夫曼编码是一种的有效的数据压缩编码。
如果没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。如0,101和100是前缀编码。由前缀码形成的序列可以被唯一的组成一个字符串序列。如00101100可以被唯一的分析为0,0,101和100。
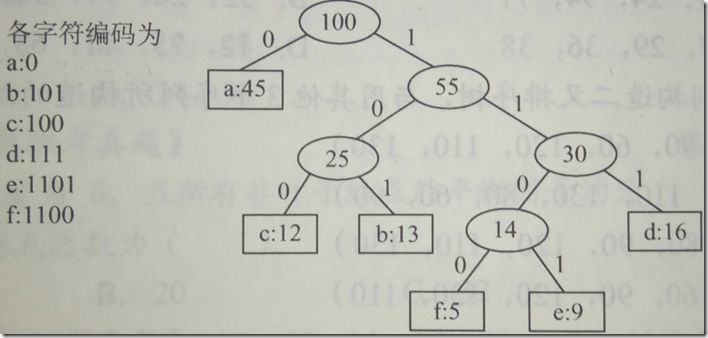
示例:
我们对一个字符串进行统计发现a-f出现的频率分别为a:45,b:13,c:12,d:16,e:9,f:5,我们对该字符串进行采用哈夫曼编码进行存储。
WPL = 1x45+3x(13+12+16)+4x(5+9)=224
这样算下来使用224二进制位就可以将该字符串存储起来,因为哈夫曼码是前缀码,所以可以唯一的还原出原来的字符序列。如果我们每个字符使用3位进行存储(至少3位),那么需要300bit才能将该字符串存储下。
* 经过左结点的值为0,经过右结点的值为1, 结点结构体中追加 string m_strCode; 经过一个分支结点,在 m_strCode 后面追加 0\1 字符,也可以根据节点,逆序寻找父结点,根据 posflag 中的值,在 m_strCode 后面追加 0\1 字符。
【扩展问题】
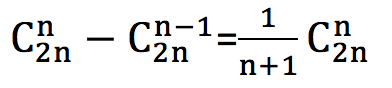
相关扩展--- set 与 优先队列 priority_queue
按照分值从大到小输出
#include<iostream>
#include<set>
#include<string>
using namespace std;
struct Info
{
string name;
double score;
bool operator < (const Info &a) const // 重载“<”操作符,自定义排序规则
{
//按score由大到小排序。如果要由小到大排序,使用“>”即可。
return a.score < score;
}
};
int main()
{
set<Info> s;
Info info;
//插入三个元素
info.name = "Jack";
info.score = 80;
s.insert(info);
info.name = "Tom";
info.score = 99;
s.insert(info);
info.name = "Steaven";
info.score = 60;
s.insert(info);
set<Info>::iterator it;
for(it = s.begin(); it != s.end(); it++)
cout << (*it).name << " : " << (*it).score << endl;
return 0;
}
/*
运行结果:
Tom : 99
Jack : 80
Steaven : 60
*/
优先队列 priority_queue从小到大输出
#include <iostream>
#include <queue>
using namespace std;
class T {
public:
int x, y, z;
T(int a, int b, int c):x(a), y(b), z(c)
{
}
};
bool operator < (const T &t1, const T &t2)
{
return t1.z < t2.z; // 按照z的顺序来决定t1和t2的顺序
}
main()
{
priority_queue<T> q;
q.push(T(4,4,3));
q.push(T(2,2,5));
q.push(T(1,5,4));
q.push(T(3,3,6));
while (!q.empty())
{
T t = q.top();
q.pop();
cout << t.x << " " << t.y << " " << t.z << endl;
}
return 1;
}
结束