数据结构 第五章 树-特殊二叉树
{ 特殊二叉树}
[满二叉树]
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
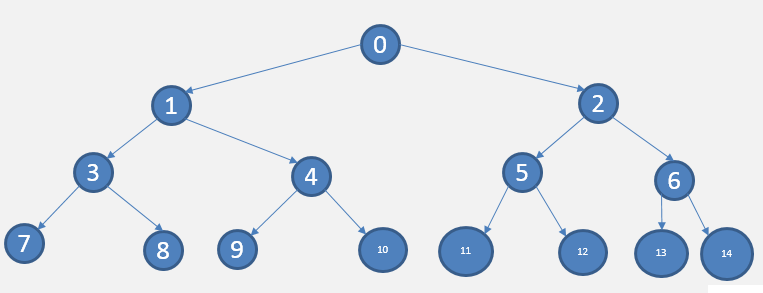
高度为h的满二叉树,结点总数 n = 2h -1 / (2 - 1) = 2h - 1
满二叉树可以以线性表的形式存储:
索引为 i 的结点,左孩子结点索引为 2i+1 ,右孩子结点的索引为 2i + 2。{索引是从上到下,从左到右}
[完全二叉树]
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
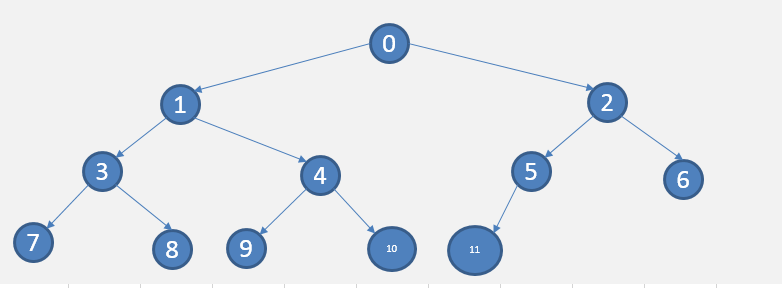
性质:
1. n为结点总数, i为结点所在的索引,索引起始值为0, i <= (n-1)/2 则 i为分支结点, i > (n-1) / 2 则i索引所对应的结点为分支结点。
2. 索引为 i 的结点,左孩子结点索引为 2i+1 ,右孩子结点的索引为 2i + 2。{索引是从上到下,从左到右}
3. 叶子结点只可能在层次最大的两层上出现。
4. 如果存在度为1的结点,那么其子节点一定为叶结点。
5. 索引值i的结点T, i为奇数,T为左孩子结点;i为偶数,T为右孩子结点。
6. 索引为 i值的结点T所在的层次为 Level = log2(i+1) , 层次起始值是0 。 推导, 满 m叉树结论 logm(n(m-1)+1) <= h < logm(n(m-1)+1) +1 ==> log2(n+1) -1 <= h < log2(n+1)
完全二叉树的应用:{大小} 堆排序
[二叉排序树BST]
也称为 二叉查找树。
定义:任意结点且存在子结点的情况下,结点的值大于左孩子结点的值,小于右结点的值, V(Father) > V(Left) && V(Father) < V(Right) , 不存在结点值相等的情况。
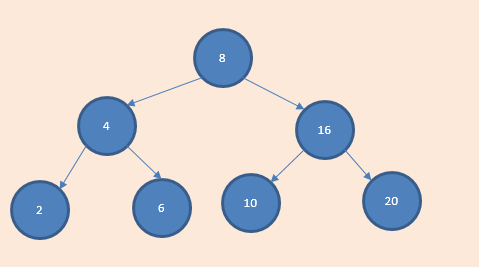
中序遍历的值为 2 4 6 8 10 16 20 ,形成了从小到大的依次排序。
BST的主要用于 查找。
查找逻辑流程图如下:
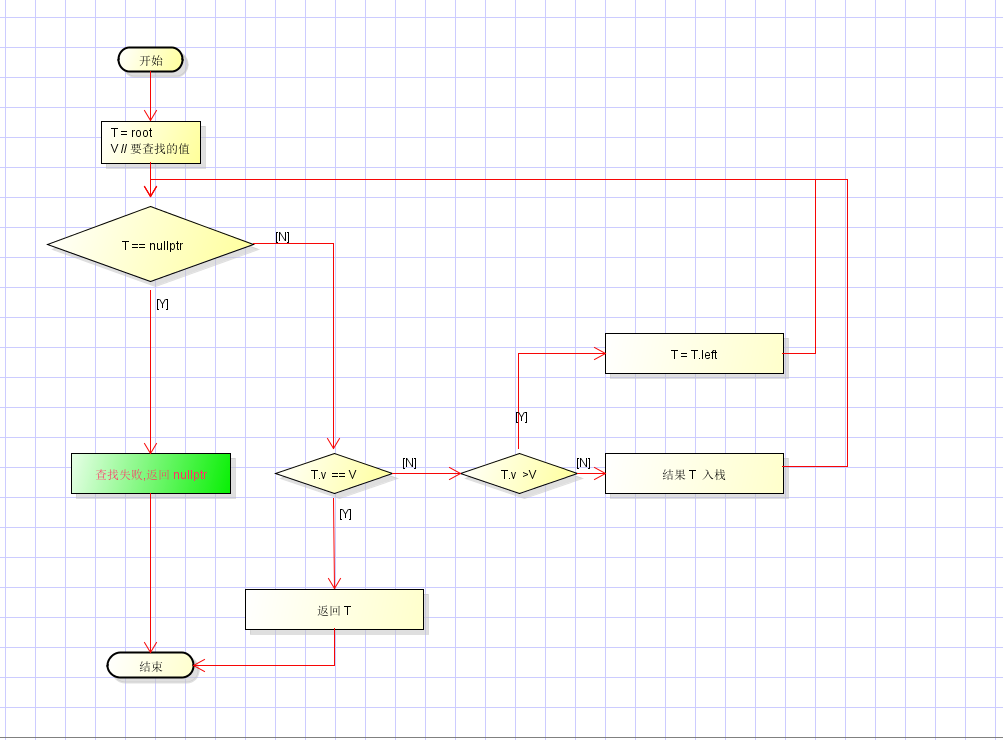
查找的时间复杂度与树的高度h相关,记为 O(h),最好的情况,BST为完全二叉树的情况下 h = log2n ,所以才有后面的AVL树。
,
{插入}
插入流程图如下:
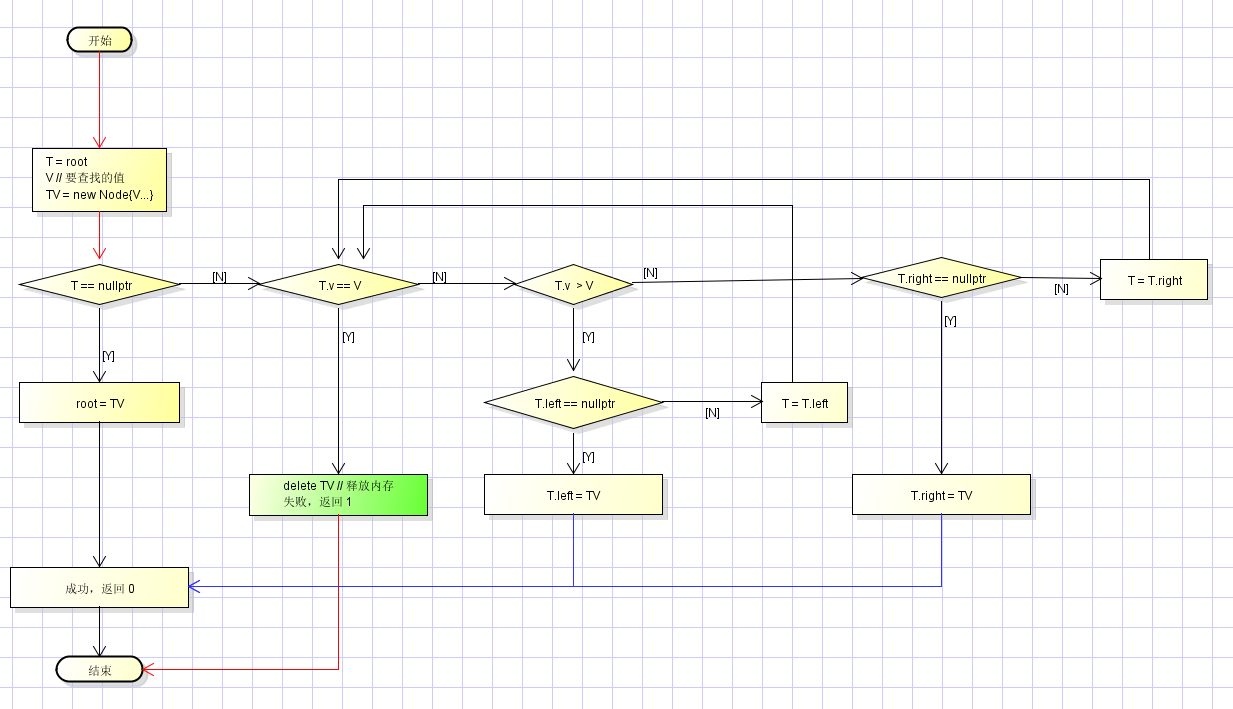
{删除}
删除数据后,再将该数据插入,产生的二叉树可能与原二叉树不相同。
删除流程图如下:
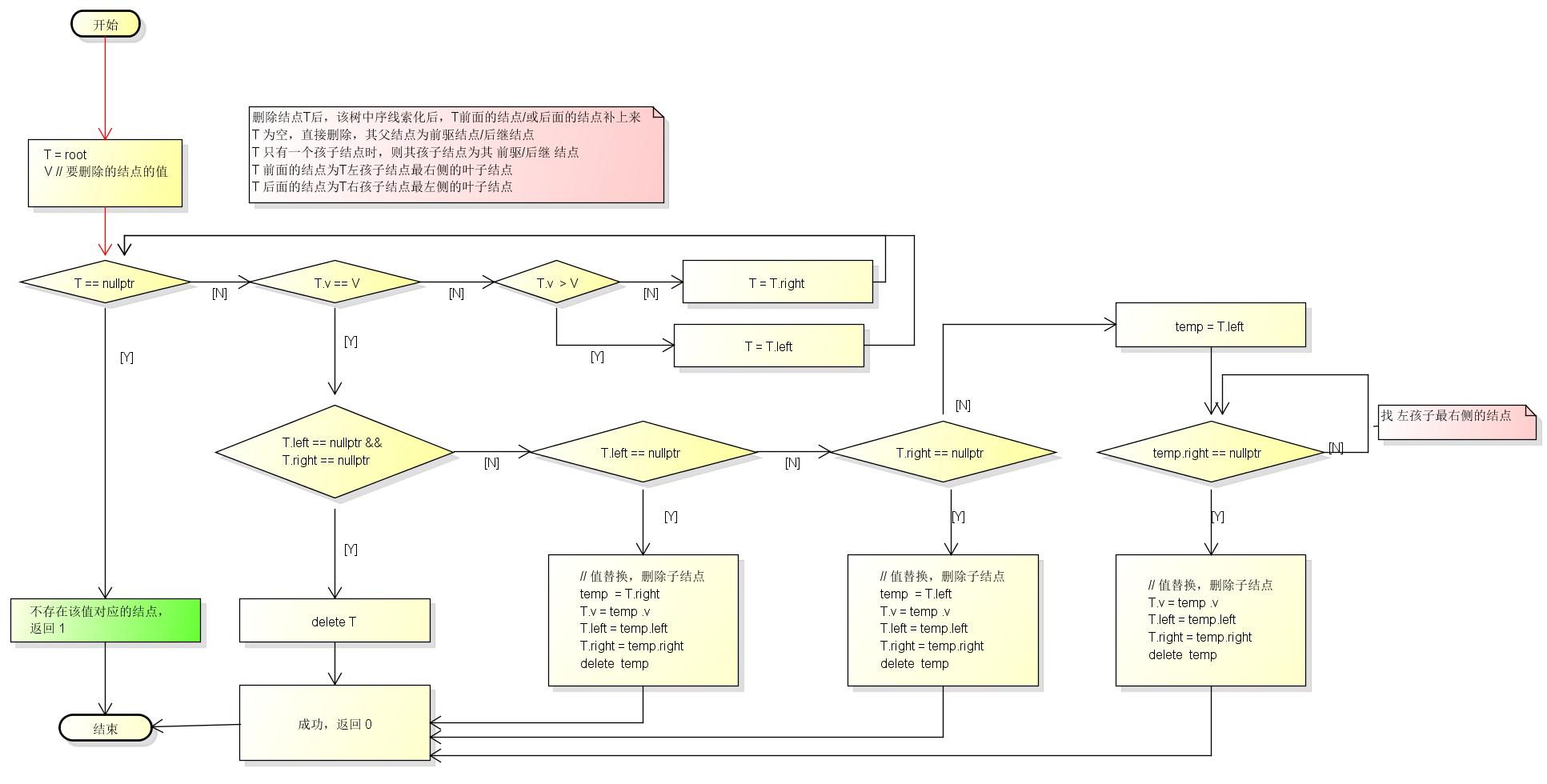
[平衡二叉树AVL树]
在 BST 的基础上,任意结点的左孩子与右孩子结点的高度差值的绝对值小于1,即 |H(L) - H(R)| <= 1
树的结点总数Nh 【其中h为树的高度】,min(Nh ) = min(Nh-1 ) + min(Nh-2 ) + 1
第0层 min( N0 ) = 1
第1层 min( N1 ) = 2
继续推导 min( N2 ) = min( N0 ) + min( N1 ) + 1 = 1 + 2 +1 = 4
这样构成一个 类似于 斐波那契数列 的 数据集合。
求最小高度使用递归或者 循环+动态规划 来实现。
AVL树结点结构形式:

【判断一棵树为 AVL树】
平衡二叉树结点的存储形式:

hight 记录结点的高度
主体思想: 使用后序遍历记录结点的高度,同时计算左右孩子结点高度的差值的绝对值是否小于等于1,若大于1,则判断该树不为 AVL树,判断函数结束。
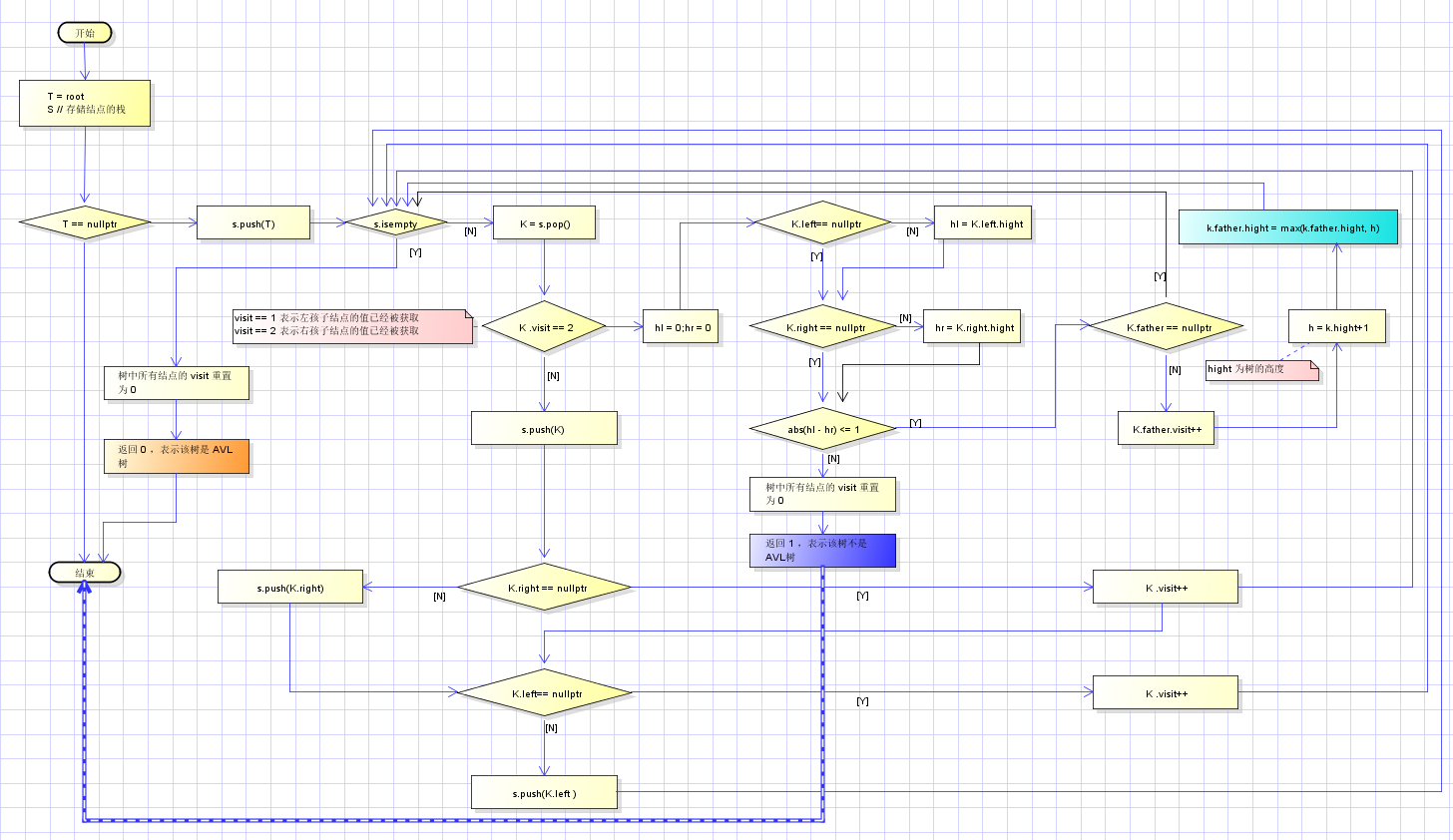
* AVL树的旋转调整*
当插入新的结点时,导致树不再是AVL树了,需要通过旋转 {不平衡处的结点},来达到新的平衡,使得新生成的树仍然是AVL树。
AVL 树平衡旋转分为: LL 右单旋转 、RR 左单旋转、 LR 先左后右旋转、RL 先右后左旋转。
以下4种AVL树插入情况及对应的旋转操作处理:
*LL平衡旋转 右单旋转
A结点的 左孩子L 的 左子树L 上插入了新的结点,导致 A的左右子树不符合AVL的差值。
旋转操作:右单旋转,以A为基点,向右旋转。
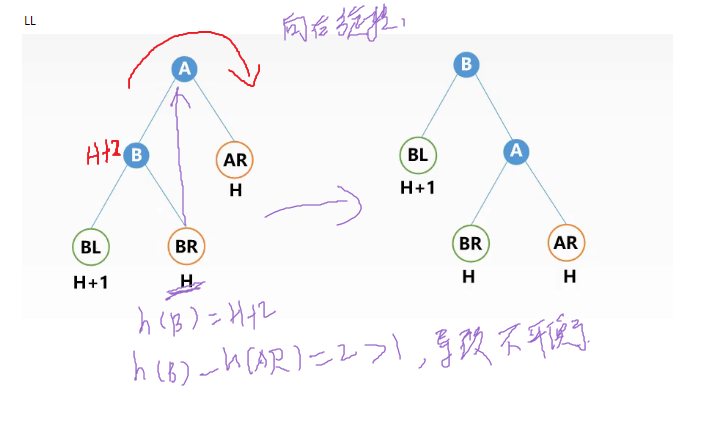
【扩展问题】LL 平衡旋转为什么叫 右单旋转?
LL 指的是导致不平衡的原因,上面红字 L L ,右单旋转 指的是旋转操作,上图中的A结点的左右子树差值超过了1,要使得树成为AVL树,需要对结点 A 单独向右旋转,所以称之为 右单旋转。
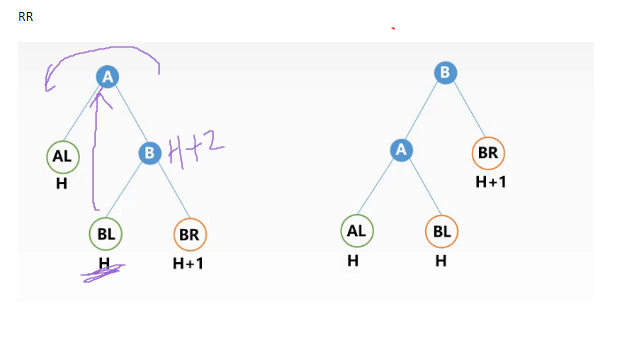
*RR平衡旋转 左单旋转
A结点的 右孩子R 的 右子树R 上插入了新的结点,导致 A的左右子树不符合AVL的差值。
旋转操作:左单旋转,以A为基点,向左旋转。
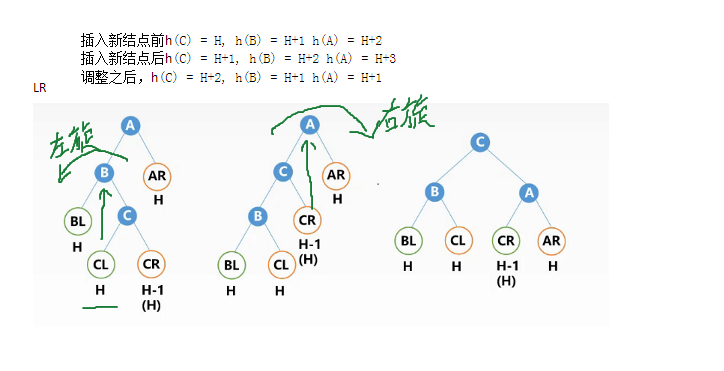
*LR平衡旋转 先左后右双旋转
A结点的 左孩子L B结点 的 右子树R 上插入了新的结点,导致 A的左右子树不符合AVL的差值。
旋转操作: 先对以B为根结点的树进行 RR 左旋操作,此时以A为根结点的树变为了 LL情况,再对以A为根结点的树进行 LL右旋操作,树调整完成。
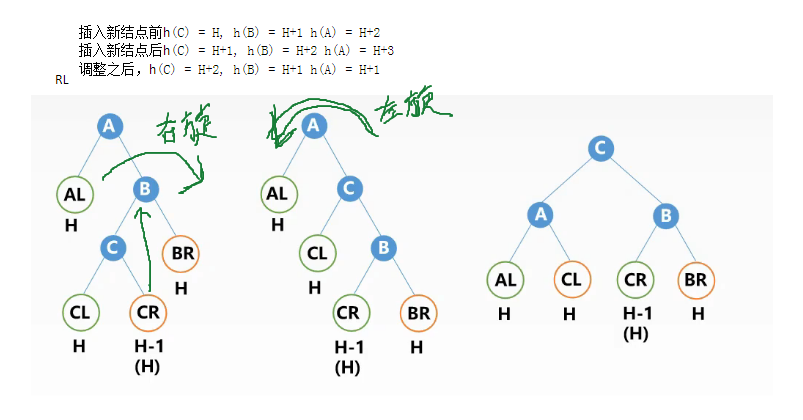
*RL平衡旋转 先右后左双旋转
A结点的 右孩子R B结点 的 左子树L 上插入了新的结点,导致 A的左右子树不符合AVL的差值。
旋转操作: 先对以B为根结点的树进行 LL 右旋操作,此时以A为根结点的树变为了 RR情况,再对以A为根结点的树进行 RR左旋操作,树调整完成。
*AVL 树插入新结点及其平衡调整的流程如下图*





