数据结构 第五章 树-二叉树及线索化
【二叉树】
二叉树 = 度为2的有序树,空树也是一种二叉树/ 一个结点(根结点)也是一种二叉树。
性质:
1. 叶子结点的树 = 度为2 的结点 + 1, 即 N(Leaf) = N(node2) + 1
推导过程:
N(all) =N(node2)+ N(node1) + N(Leaf)
N(all) =2N(node2)+ N(node1) + 1
==> N(Leaf) = N(node2) + 1
2. K层最多有 2k 个结点
【二叉树的存储】
顺序存储: 结构体数组的形式存储,适合 满二叉树 、完全二叉树。主要看结点结构体如何定义了。
链式存储:结构体指针链放入形式存储
各自优缺点:参照 线性表 章节
【二叉树的遍历】
根据父结点的访问序列,分为4种:
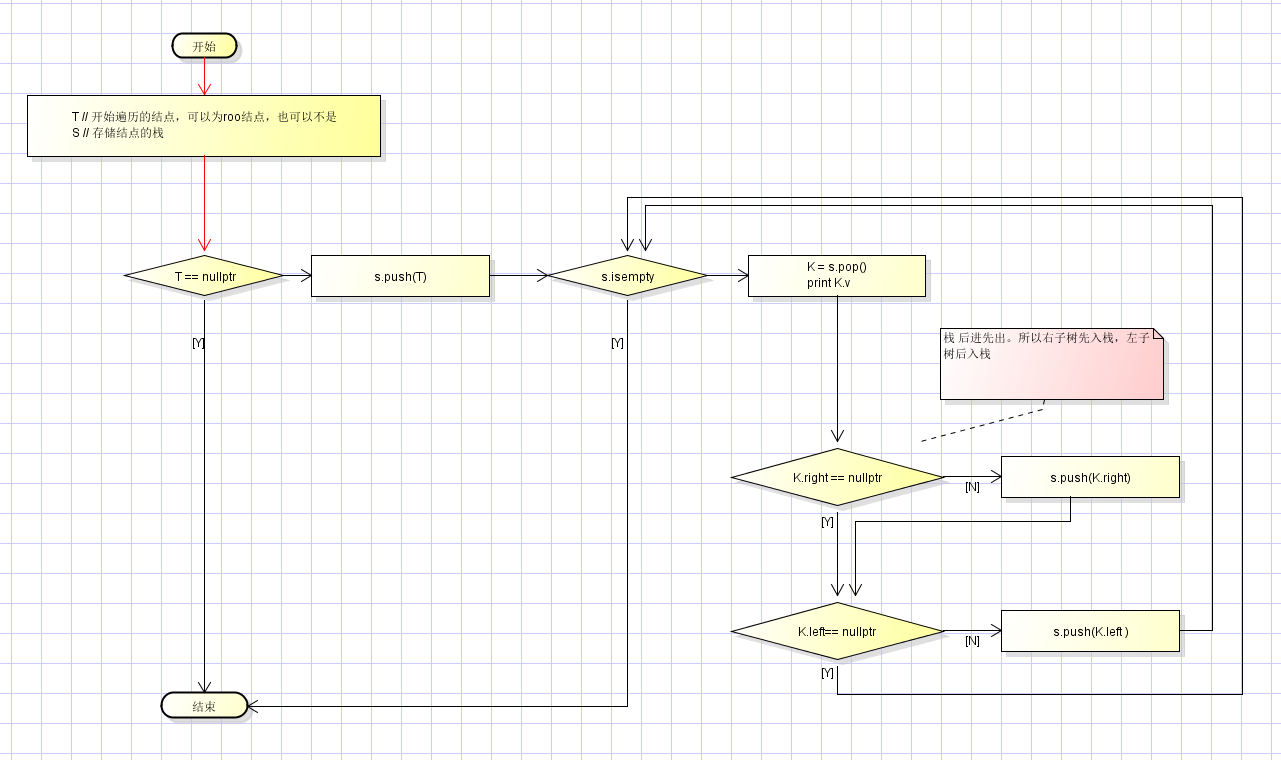
1)先序遍历\先根遍历\前序遍历,1 访问 根结点,2 访问左子树上的结点,左子树上的结点访问完成后,3 访问右子树上的结点。
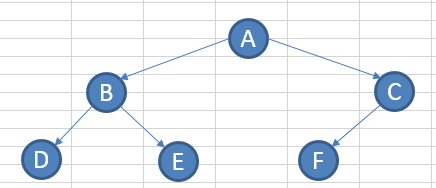
打印结果: A B D E C F
流程图如下:
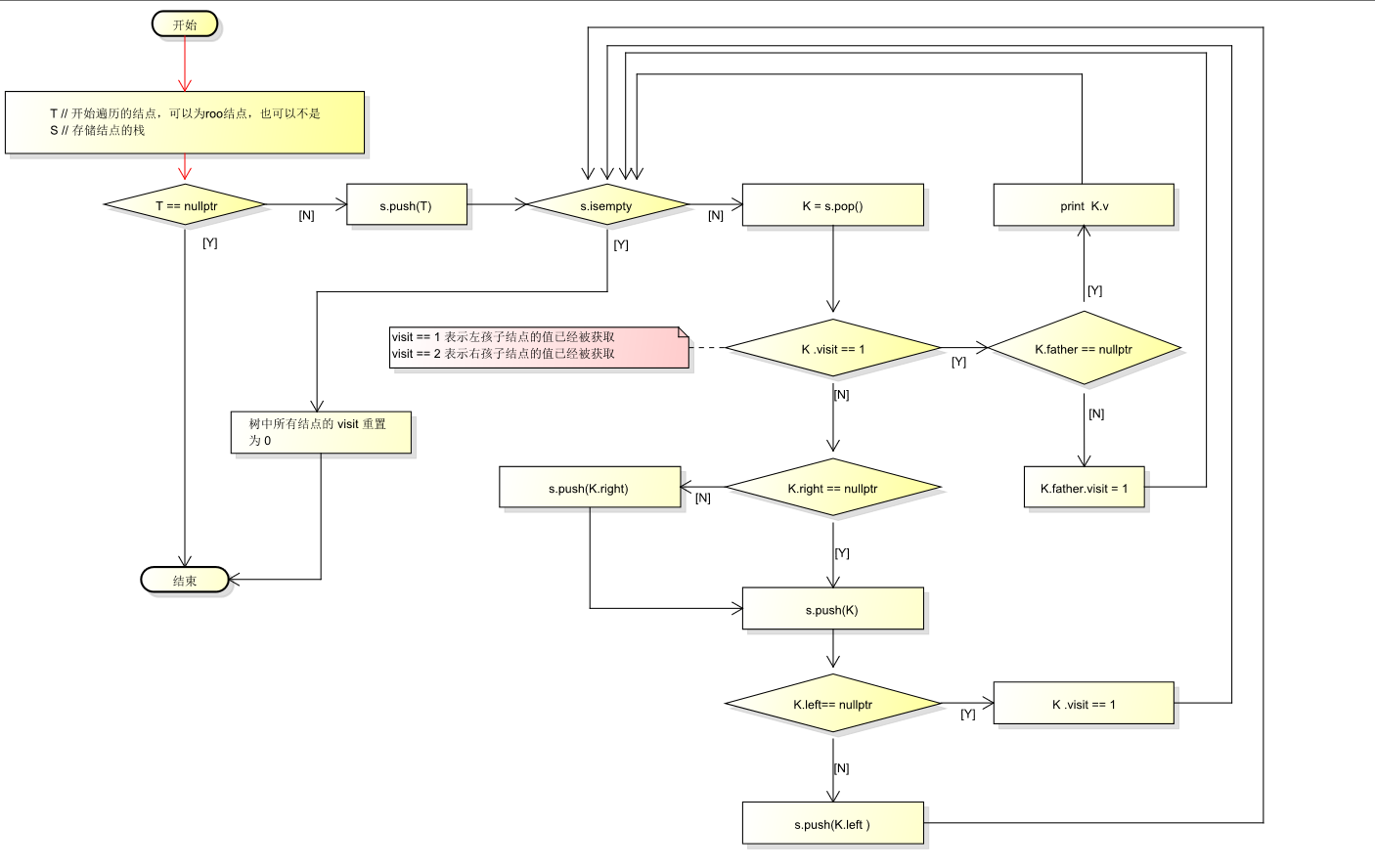
2)中序遍历\中根遍历,1 访问左子树上的结点,左子树上的结点访问完成后,2 访问 根结点,3 访问右子树上的结点。

打印结果: D B E A F C
流程图如下:
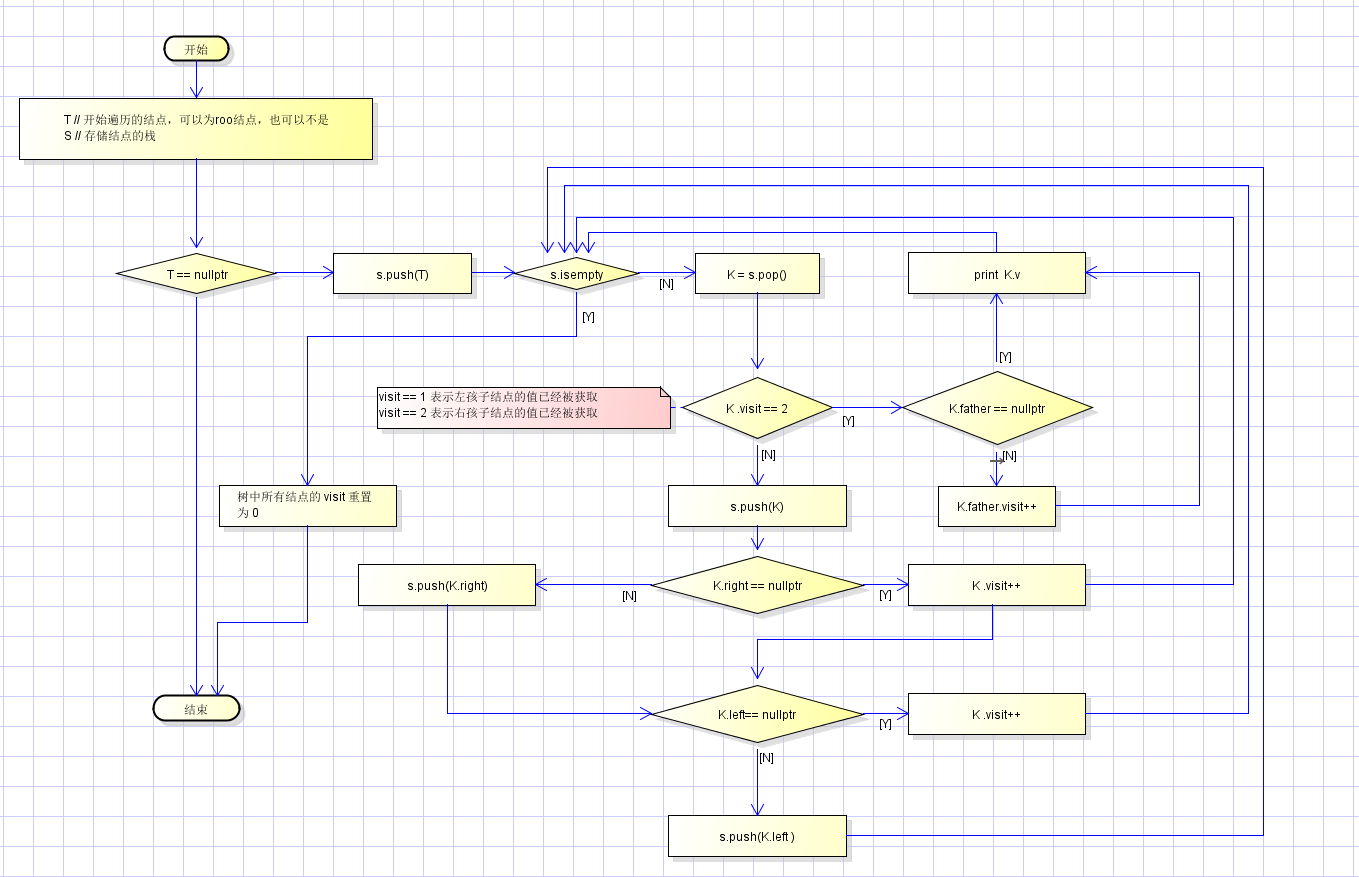
3)后序遍历\后根遍历,1 访问左子树上的结点,左子树上的结点访问完成后,2 访问右子树上的结点,3 访问 根结点。

打印结果: D E B F C A
流程图如下:
总结,树的深度遍历,可以使用递归,也可以使用栈+循环 来实现。
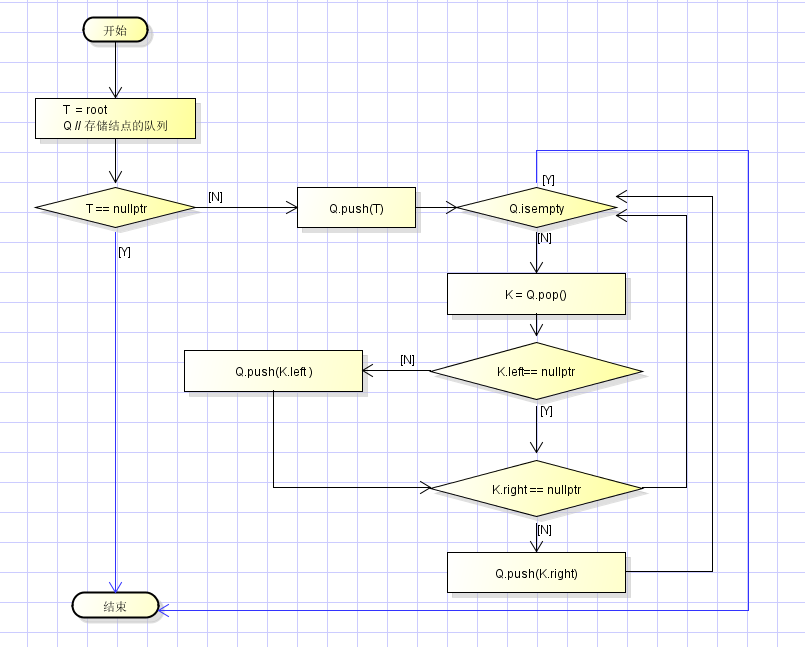
4) 层次遍历:
从二叉树的第一层(根节点)开始,从上至下逐层遍历,在同一层中,则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中,按从顶层到底层的次序访问树中元素,在同一层中,从左到右进行访问。
层次遍历流程图如下:
【线索二叉树】
在二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树以某种遍历方式(如先序、中序、后序或层次等)进行遍历,使其变为线索二叉树的过程称为对二叉树进行线索化。
树线索化后,使得树有了 前驱 后继结点,树线性化了。

ltag: 0 pleft 指向左孩子结点, 1 pleft 指向其 前驱 结点
rtag: 0 pright 指向右孩子结点, 1 pright指向其 后继 结点
根据二叉树的遍历顺序生成不同的线索二叉树,分为 先序、 中序、 后序 线索二叉树。
如下图:

先序线索化二叉树 创建流程:
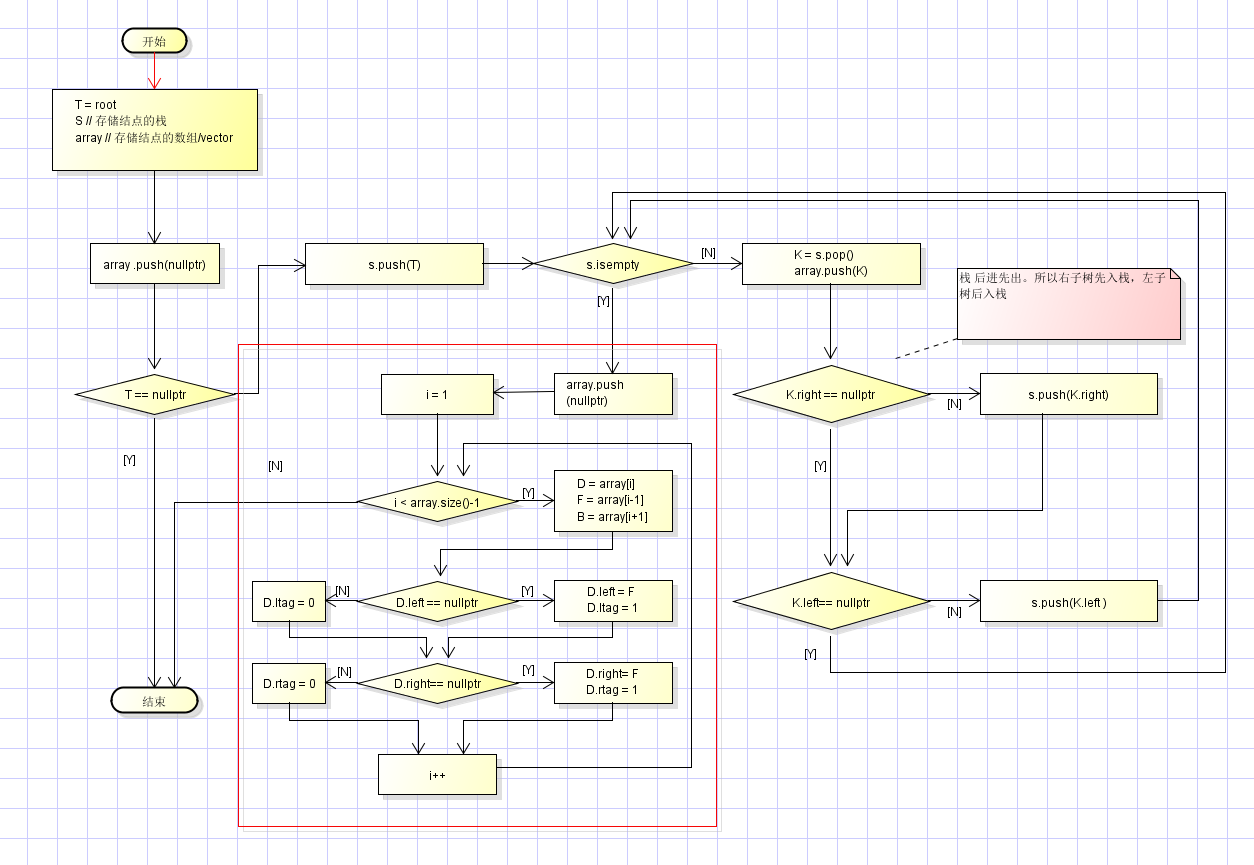
中序线索化,后序线索化流程,参照 中序、后序遍历 + 上图红框部分。




