数据结构 第五章 树-树 森林 基本概念

树 是一种逻辑结构，不是物理存储结构。是一种可递归的数据结构。

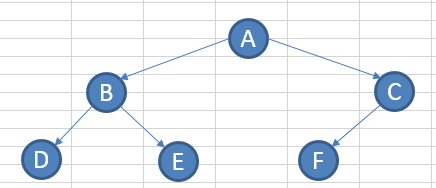
 结点数为 0 的树称为空树。

当 结点数 n > 1 时，子节点本身也是一棵树。称为该结点的 子树；上图中，B树为A结点的左子树， C为结点的树，称为A结点的右子树， A称为 根结点。 D为结点的树称为结点B 的左子树...

n 个结点的树中有 n-1 条变边。

D为 A B 结点的子孙结点，A B 为D 的祖先结点；D是B 的孩子结点，B是D E 的双亲结点，D E 是 B 的孩子结点，E和D互为兄弟结点。

 

【结点的度】

 

 定义： 结点的子节点的个数。

A结点的子节点为  B  C 结点，所以 A结点的度的 D(A) = 2， C结点的度为 D(C) = 1   ... D结点的度为 D(D) = 0（应为D没有子结点）。

树的度 = max(D(X))     X = {A B C D E F}   所以上图中，树的度为 2。

D(X) = = 0 的结点为 叶子结点； D(X) > 0 的结点为分支结点。

 

 【树的高度与深度】

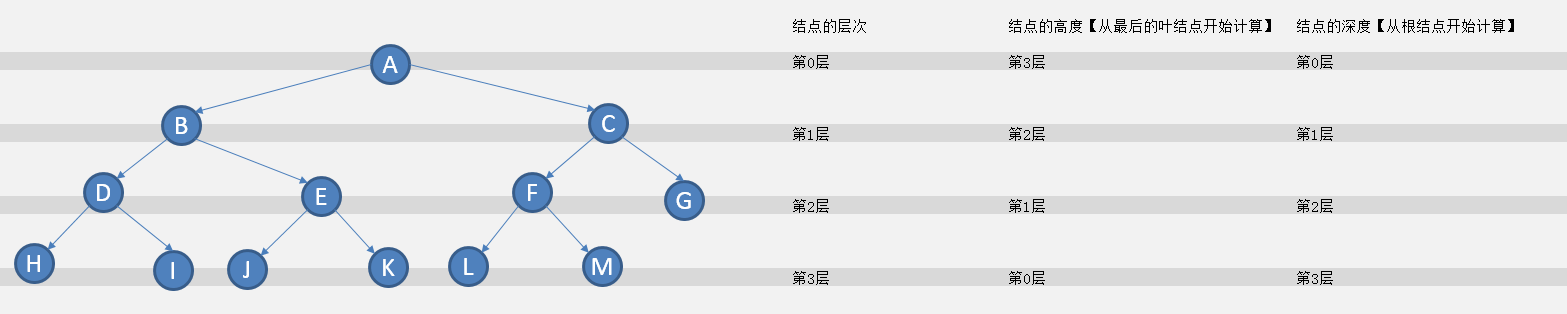
树的高度等于树的深度 等于 树中结点的最大层次

H(T) = D(T) = MAX(L(x))    x = {A B C ... M}

 

【有序树 与 无序树】 

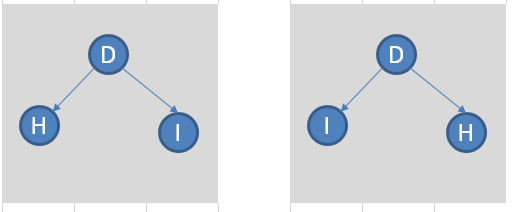
无序树的话，上面两颗树相同。

若为有序树，则上面两棵树不相同，第一张图中 H为D 的左子树 ，而在第二张图中，H 为 D 的右子树。

 

【路径 路径长度】 

 

 

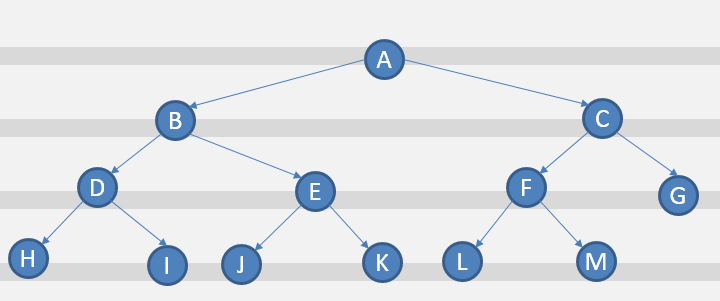
路径：两个结点间的结点所构成的序列 A H 结点的路径为 A B D H ; 路径是有向的，方向为 自上而下。

路径长度：路径所构成的边的数量，A H 的路径长度为 3，分别为 A->B  B -> D D->H

【森林】 

 

 多棵树 组成 森林。

 森林追加 一个共同的根结点构成树。

 

 【树的性质】

1 . 树的结点数 = 所有结点的度 + 1 ，  其中 1 为根结点

2. 度为 m 的树，第 i 层最多有 m^i-1 个结点，如下图 满三叉树：

3. 高度为h的m叉树，最多有D 个结点： 

等比数列求和：D = m⁰ + m¹ + m²+ m³ + m⁴ + m⁵ + ... +m^h-1  = （m^h - 1）/ (m-1)

4 由性质3逆向推理：

n个结点的m叉树的最小高度为 h =  ^Γ log_m^(n(m-1)+1)  ，因为h为整数，所以取整，使用 取上界取整函数，原因及推导过程：

树的高度最小，那么，除最后一层，其它层都满，则有

（m^h-1 - 1）/ (m-1)  < n <= （m^h - 1）/ (m-1)           ==>     log_m^(n(m-1)+1)   <= h <  _{^{logm(n(m-1)+1)}} +1， 所以 h 为 log_{m^{(n(m-1)+1)的值}}  取上界整数。 层次从 1开始，若层次从0开始计算，则  log_m^(n(m-1)+1) -1  <= h <  _{^{logm(n(m-1)+1)  。}}

 

结束