数据结构 第三章的扩展 特殊矩阵--压缩存储
一维数组的存放形式:

二维数组的存放形式:
行优先原则(C语言数组内存分配)

列优先原则(fortran 语言内存分配)

矩阵可以看做是二维数组,二维数组以某种优先原则的形式存储为一维数组。如果矩阵中有某些相同规律且重复的元素,转为一维数组时,删掉重复元素,从而实现压缩存储。
以下存储都已行优先原则存储。
【对称矩阵】
沿左对角线对称的矩阵。
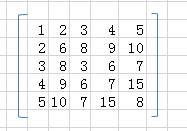
特点: A[i][j] == A[j][i]
需要一维数组的大小:
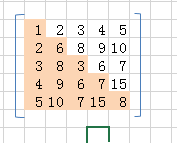
行优先存储,按行计算元素个数。
1 + 2 + 3 + 4 + 5 = 5 *(1 + 5 ) / 2 = 15
归纳 n*n的对称矩阵需要的一维数组大小:
1 + 2 + 3 + ... + n = n * (1 + n) / 2
二维转一维简要代码:
k = 0;
m = n * (1 + n) / 2;
B[m];
for i = 0; i < n; i++
for j = 0; j <= i; j++
B[k++] = A[i][j]
一维转二维:
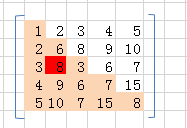
设 A[i][j] = = B[k],那么,i行前面的 i-1 行元素,因为从0行开始,第i-1行有 i-1 + 1 个元素列数满足 MAX(col) == row的,即,1 + 2 + ... + i 个元素
所以: k = 1 + 2 + ... + i-1 + j = i*(i+1) / 2 + j
一维转二维数组简码:
for i = 0; i < n; i++
for j = 0; j <= i; j++
k = i*(i+1) / 2 + j;
A[i][j] = B[k];
A[j][i] = B[k];
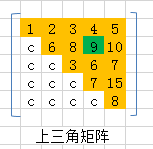
【三角矩阵】

上三角矩阵:
i > j , A[i][j] = 常量
else, A[i][j] = 其他值
下三角矩阵:
i < j , A[i][j] = 常量
else, A[i][j] = 其他值
以上三角矩阵为例:
归纳 n*n的三角矩阵需要的一维数组大小:
n + n-1 + ... + 1 = n * (1 + n) / 2 + 1 ,其中1 为存储下三角区常量值。
二维转一维简要代码:
k = 0;
m = n * (1 + n) / 2 + 1;
B[m];
for i = 0; i < n; i++
for j = 0; j < n-i; j++
B[k++] = A[i][j]
B[m-1] = c;
一维转二维:
设 A[i][j] = = B[k],那么,i行前面的 i-1 (i > 0)行元素,因为从0行开始,第i-1行有 n-i +1 个元素列数满足 MAX(col) == row的,即,n + n-1 + ... + n-i +1个元素, 索引为 i行前面有 i行,因为行号从 0 开始。
所以: k = n + n-1 + ... + n-i +1 = (2n - i + 1)/ 2 * i + j - i
一维转二维数组简码:
for i = 0; i < n; i++
for j = 0; j < n- i; j++
A[i][j] = B[m-1] ;
for i = 0; i < n; i++
for j = 0; j < n- i; j++
if i == 0 k = j;
else k = (2n - i + 1) / 2 * i + j - i;
A[i][j] = B[k];
【三对角矩阵 又叫 带状矩阵】
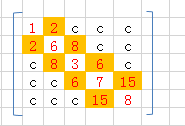
i - j >1 || j - i > 1, A[i][j] = 常量
else, A[i][j] = 其他值
归纳 n*n的三对角矩阵需要的一维数组大小[大小都为常量]:
2 + 3 + 3+... + 3 +2 +1 = (3-1)+ 3 + 3+... + 3 + (3-1) +1 = 3n -2 + 1 ,其中1 为存储带状以外的常量值。
二维转一维简要代码:
k = 0;
m = 3*n -2 + 1;
B[m];
for i = 0; i < n; i++
for j = 0; j < n; j++
if i - j >1 || j - i > 1 continue;
B[k++] = A[i][j]
B[m-1] = c;
一维转二维:
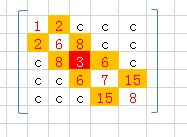
设 A[i][j] = = B[k],那么,i行前面的 i-1 (i > 0)行元素,因为从0行开始,0行有 2个元素,从 1行开始,有3个元素,前 i- 1 行总共有 3(i-1)+2 , i > 1。第i行, j元素下标为 j-i+1
所以: k = 3(i-1)+2 + j-i+1
一维转二维数组简码:
for i = 0; i < n; i++
for j = 0; j < n- i; j++
A[i][j] = B[m-1] ;
for i = 0; i < n; i++
for j = 0; j < n; j++
if i - j >1 || j - i > 1 continue;
if i == 0 k = j;
else k = 3(i-1)+2 + j-i+1
A[i][j] = B[k];
补充:
i = (k+1 )/ 3
j = k - 2i
【稀疏矩阵】
有效数据比较少的矩阵,如下图:
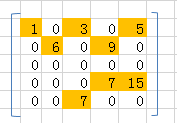
表示方法,十字链表法
struct head {
type* rownext;
type value;
type* colnext;
}
为形象表示,分为行头和列头
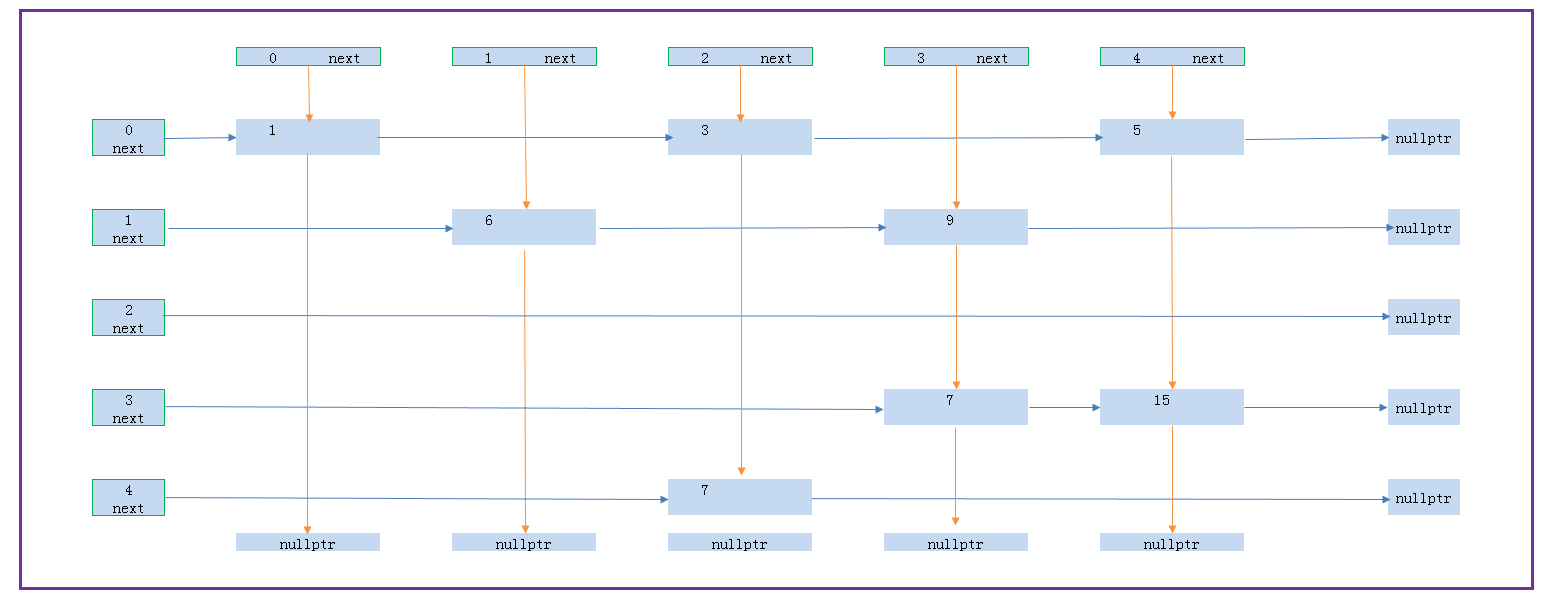
后面的稀疏图表示也要用到 十字链表法。
结束。




