数据结构 第三章 栈 和 队列
栈和队列 都是一种受限的线性表。
【栈】stack
特性: 先进后出的线性表 LIFO
比如:放盘子,最后放上去的,最先取下来。

基本操作函数:
init() : 创建 destroy():销毁 push():插入数据 top(): 取得栈顶元素 pop(): 删除栈顶元素 isEmpty(): 判空,栈是否为空
n个数据入栈,数据出栈的种类个数,使用卡特兰公示:(1/(n+1)) * Cn2n

【顺序栈】
使用顺序表来实现:
struct statck{
type data[100];
type top; 数组索引,即栈顶元素的索引, top == -1, 栈空
}

【链栈】
struct statck{
type *pdata;
type *pbottom;
type* ptop; 数组索引,即栈顶元素的索引, top == -1, 栈空
}

【栈的应用】
IDE环境中符号匹配问题
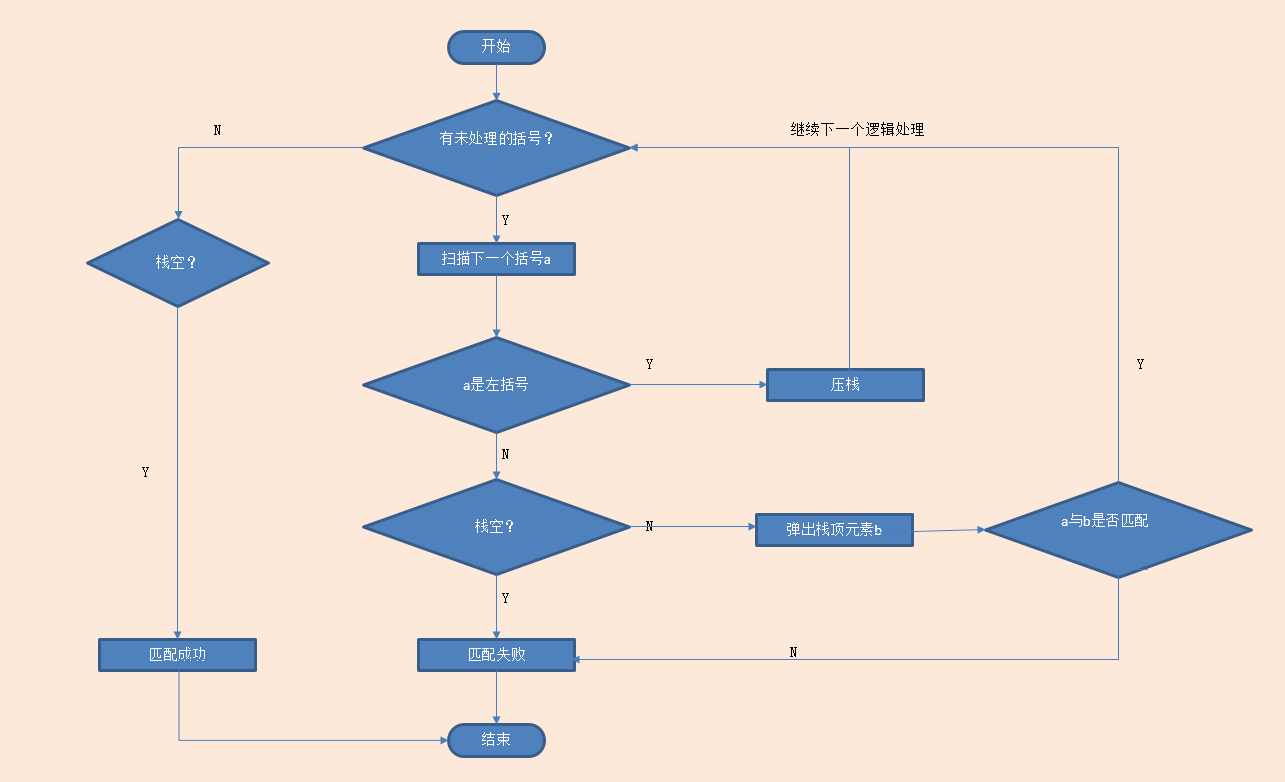
四则运算中 界限符(括号) 匹配问题
四则运算的计算
【栈-四则运算】
表达式由, 操作数、操作符、界限符 构成

数学表达式形式分为以下三种:
中缀表达式: ( 15 / ( 7 - ( 1 + 1 ) ) * 3 ) - (2 + ( 1 + 1 ) )
前缀表达式【波兰式】: - * / 15 - 7 + 1 1 3 + 2 + 1 1
后缀表达式【逆波兰式子】: 15 7 1 1 + - / 3 * 2 1 1 + + -
其中常用的计算机表达式为 逆波兰式。
详细转换过程:
中缀转前缀 :
从右向左扫描字符串,将表达式转为 后缀表达式 T(X), 将T(x) 逆序,即,转换为前缀表达式。
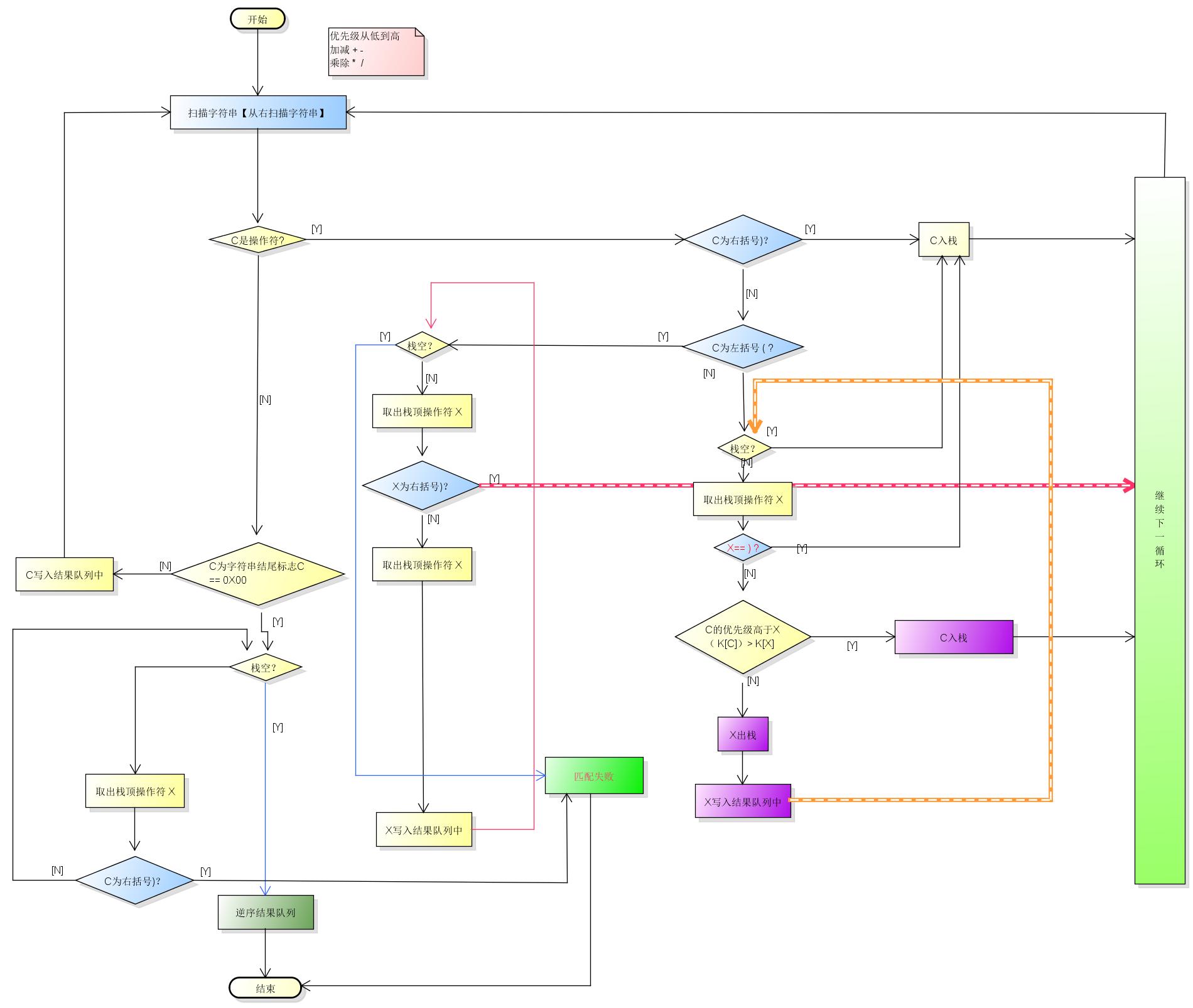
实现过程如下:

前缀计算过程:
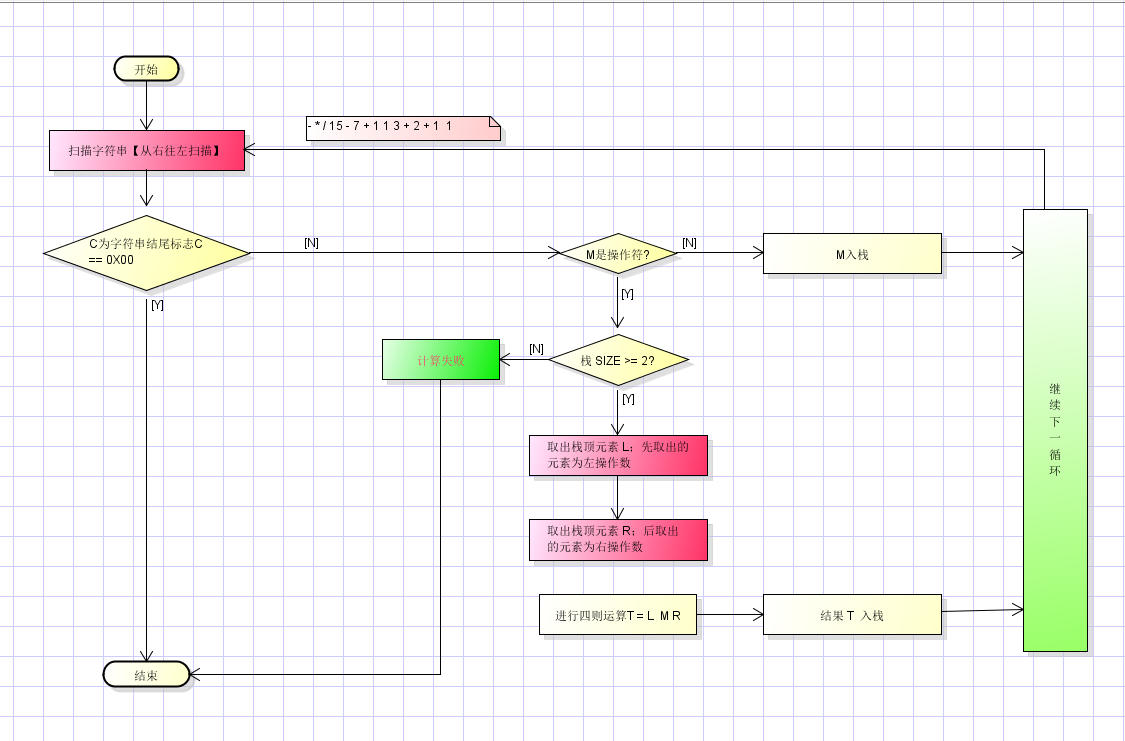
计算过程 同时也是 后缀转中缀 的过程;类似于下面的后缀计算过程,详细看后缀。此处不写了。
中缀转后缀:
操作符入栈,遇到限定符或栈顶元素的优先级较高,则栈顶元素出栈,新操作符入栈。具体流程如下:
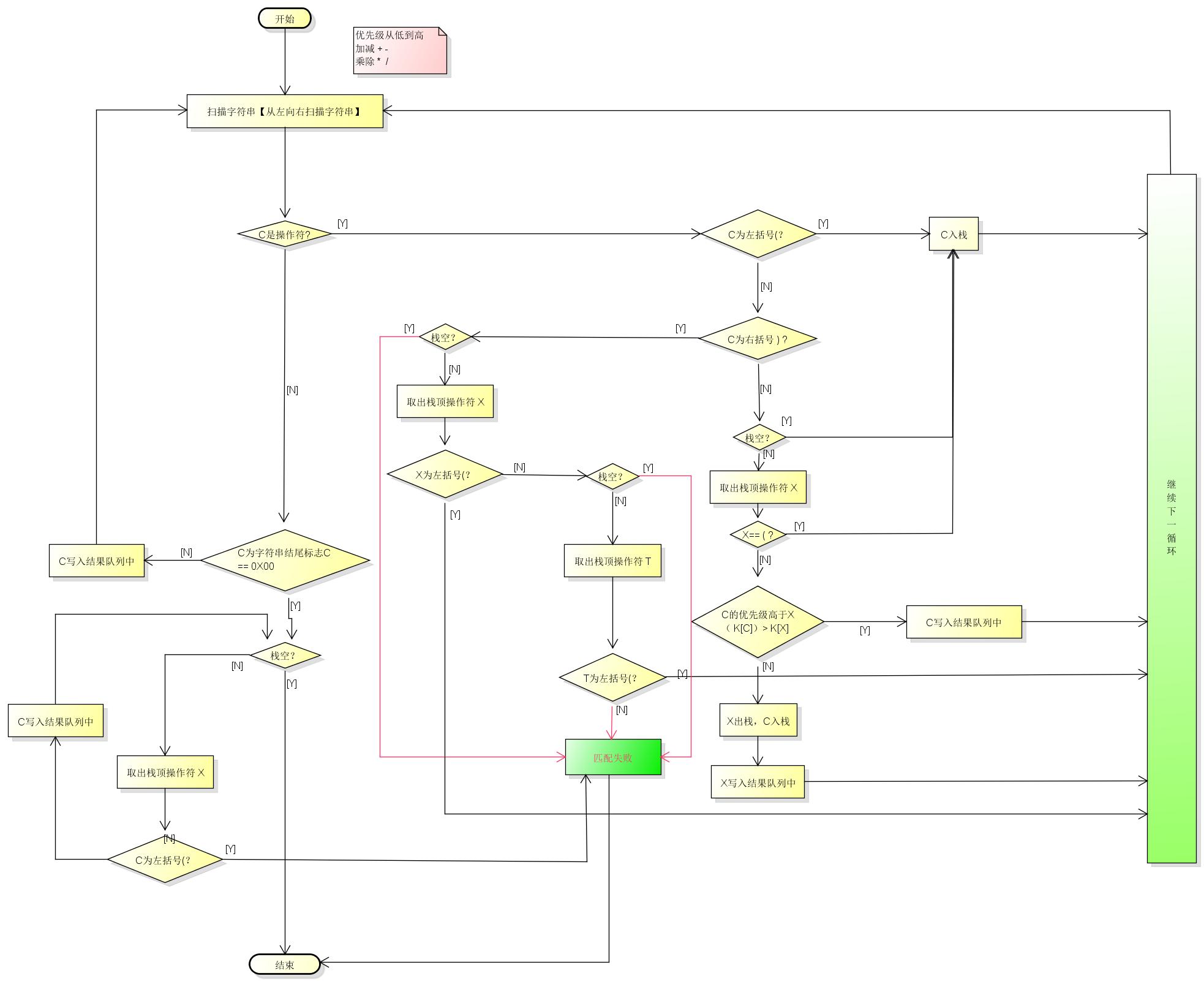
详细操作流程:
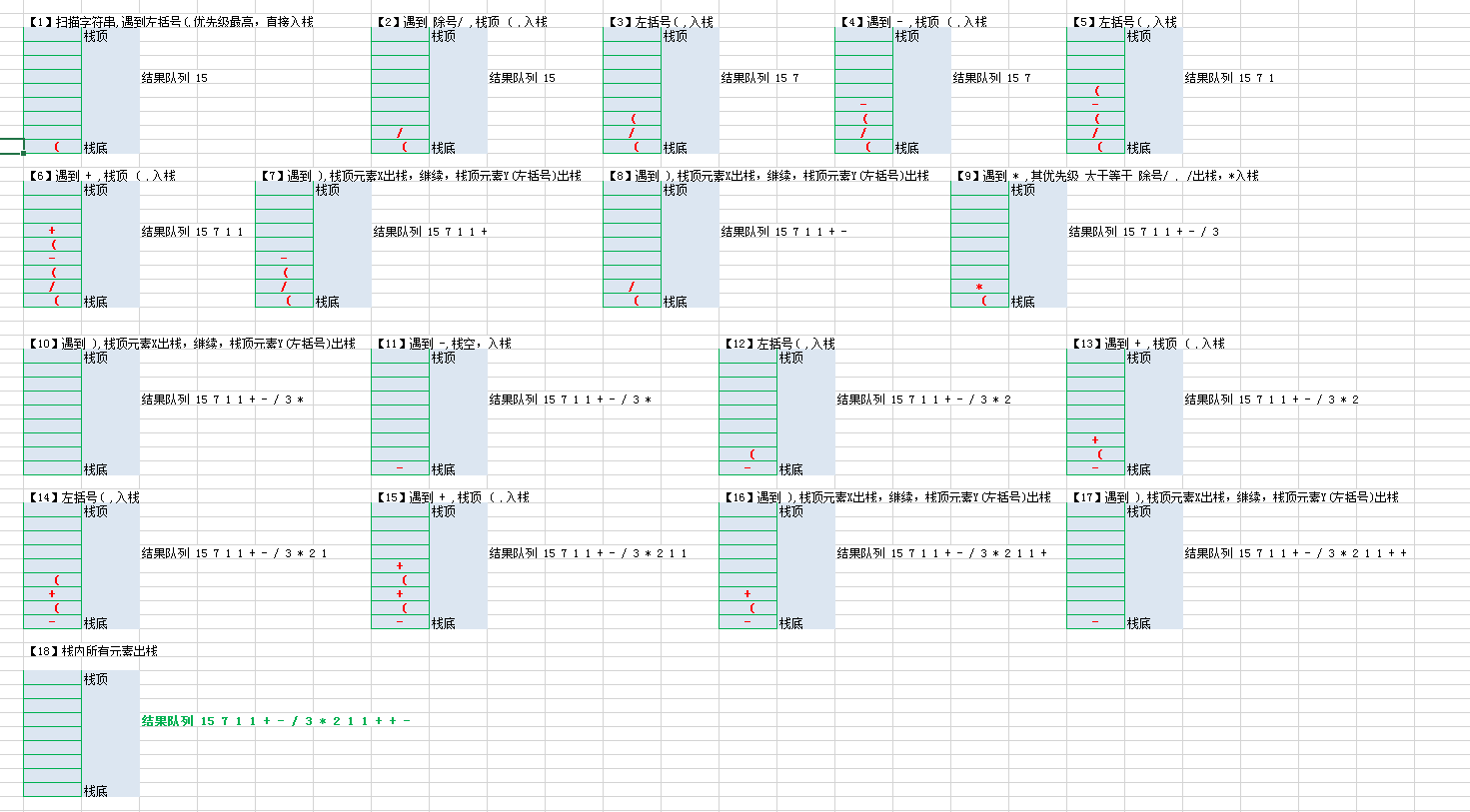
后缀 表达式计算:
操作数入栈,遇到操作符,执行相应的操作,把结果压入栈中,继续下一循环。注意:先出栈的操作数为右操作数,后出栈的为左操作数。具体流程如下:

具体操作【同时也是 后缀转中缀 的过程】:

【栈在递归中的应用: 函数调用栈】
如下图:
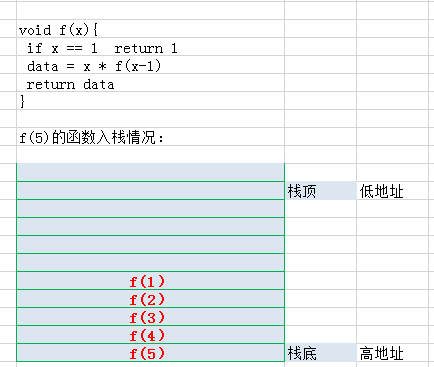
计算 f(5)时,f(5)中调用 f(4),f(4)调用f(3),...f(1)结束,然后从f(1)依次弹出栈,f(5)函数计算完成.
函数栈中存放的是函数执行过程中所需要的内存栈空间,即局部变量所占内存空间。他是根据代码区的指令进行分配。
递归解决的问题:问题属性相同且规模较小。例如: 阶乘、斐波那契数列
优点:找到问题属性,实现代码,依次调用,写代码方便。
缺点:函数调用栈溢出。重复计算,效率低。
可以用动态规划、栈、for循环 代替递归调用。
【队列】queue
先进先出(FIFO—first in first out)线性表。 前端(front)进行删除操作,而在表的后端(rear)进行插入操作。
基本操作函数:
init() : 创建 destroy():销毁 push():插入数据 top(): 取得队头元素 pop(): 删除队头元素 isEmpty(): 判空,队列是否为空
【顺序队列】
struct statck{
type data[100];
type front; 队头索引 front = (front+1) % 100
type rear; 队尾索引 rear= (rear+1) % 100
type num; num == 0是,队列为空
}

由于内存分配固定,队头/尾的索引需要向后递增,所以需要 %100 来实现 循环队列,同样防止索引递增下去引起的数组越界。
【链队列】
struct statck{
type *pdata;
type *pfront; 队头指针
type *prear; 队尾指针
// type *pnext; 插入元素的下一个数据内存,该变量实现循环队列;如果队列的基类本生就是循环链表的话,不需要使用该变量,因为他本身就是循环队列。
type num; num == 0是,队列为空
}

【双端队列】: 分别供两端插入或删除
扩展:
只能从一端输入,两端可以输出的双端队列【输入受限的双端队列】
只能从一端输出,两端可以输入的双端队列【输出受限的双端队列】
应用:
* 求回文
* 求平衡问题
【队列的应用:】
树的层次遍历:
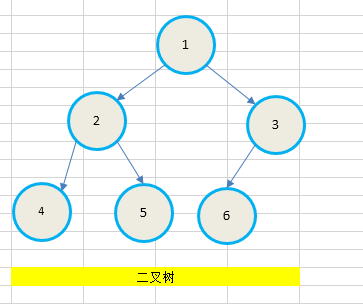
遍历过程:
① 入队列,
①出队,左右孩子结点②③入队, 结果①
②出队,左右孩子结点 ④⑤入队,结果①②
③出队,左右孩子结点⑥入队,结果①②③
④出队,左右孩子结点为空,无元素入队,结果①②③④
⑤出队,左右孩子结点为空,无元素入队,结果①②③④⑤
⑥出队,左右孩子结点为空,无元素入队,结果①②③④⑤⑥
队列为空,结束。
树的层次遍历完成。
图的广度优先遍历 BFS:
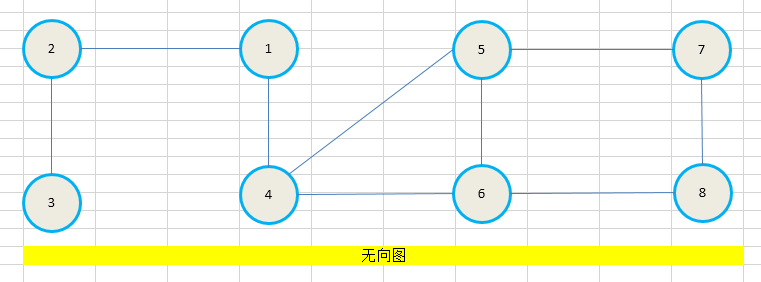
遍历过程:
① 入队列,结点flag设置为1
①出队,孩子结点②④入队,结点flag设置为1,结果①
②出队,孩子结点 ③入队,结点flag设置为1,结果①②
④出队,孩子结点⑤⑥入队,结点flag设置为1,结果①②④
③出队,无孩子结点,结果①②④③
⑤出队,⑥结点flag为1,不入队,⑦结点入队,结点flag设置为1,结果①②④③⑤
⑥出队,⑤结点flag为1,不入队,⑧结点入队,结点flag设置为1,结果①②④③⑤⑥
⑦出队,⑤⑧结点flag为1,不入队,结果①②④③⑤⑥⑦
⑧出队,⑥⑦结点flag为1,不入队,结果①②④③⑤⑥⑦⑧
队列为空,结束。
BFS完成。
队列在操作系统中的应用:
多个进程争夺系统资源时,常用策略--> FCFS(FIRST COME FIRST SERVICE) 先来先服务。
打印机的缓冲区,可以使用优先队列,设置打印权限。
【四则运算的实现】
【类图】
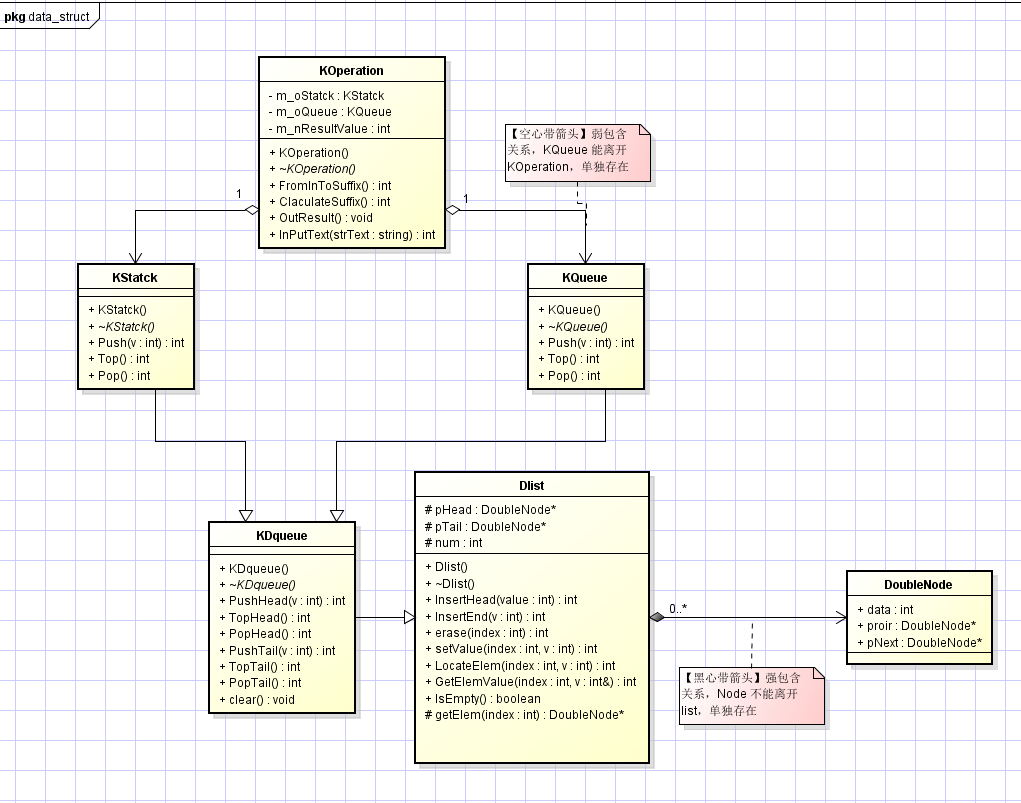
【实现代码】
Dlist.h
#pragma once
using namespace std;
using DoubleNode = struct _dNode
{
int data;
struct _dNode* pProir;
struct _dNode* pNext;
};
// 双向链表
class Dlist
{
public:
// init 放到构造函数中
Dlist();
// destroy 放到析构函数中
virtual ~Dlist();
// 前插数据
int InsertHead(int value);
// 后插数据
int InsertEnd(int value);
// 删除元素
int erase(int index);
// 设定元素值
int setValue(int index, int value);
// 查找从Index 后面值为value的元素的索引
int LocateElem(int index, int value);
// 查找从Index 的值
int GetElemValue(int index, int& value);
// 判断链表是否为空
bool IsEmpty();
// 链表长度
int Size();
protected:
// 取得下标为 index 的元素
DoubleNode* getElem(int index);
protected:
DoubleNode* pHead;// 表头
DoubleNode* pTail;// 表尾
int num;// 元素的个数
};
#include "Dlist.h"
Dlist::Dlist()
{
pHead = new DoubleNode{0, nullptr, nullptr};// 表头
pTail = new DoubleNode{0, nullptr, nullptr};// 表尾
pHead->pNext = pTail;
pTail->pProir = pHead;
num = 0;// 元素的个数
}
Dlist::~Dlist()
{
while (pHead->pNext !=nullptr)
{
DoubleNode* Elem = pHead->pNext;
pHead->pNext = Elem->pNext;
delete Elem;
}
delete pHead;
}
// 前插数据
int Dlist::InsertHead(int value)
{
DoubleNode* Elem = new DoubleNode{value, nullptr, nullptr};
num++;
Elem->pNext = pHead->pNext;
Elem->pProir = pHead;
pHead->pNext = Elem;
Elem->pNext->pProir = Elem;
return 0;
}
// 后插数据
int Dlist::InsertEnd(int value)
{
DoubleNode* Elem = new DoubleNode{value, nullptr, nullptr};
num++;
Elem->pProir = pTail->pProir;
Elem->pNext = pTail;
Elem->pProir->pNext = Elem;
pTail->pProir = Elem;
return 0;
}
// 取得下标为 index 的元素
DoubleNode* Dlist::getElem(int index)
{
if ((index >= num) || nullptr == pHead)
{
return nullptr;
}
// 第0号元素
DoubleNode* Elem = pHead->pNext;
// 找到指定元素
while (index >= 1)
{
Elem = Elem->pNext;
index--;
}
return Elem;
}
// 删除元素
int Dlist::erase(int index)
{
DoubleNode* Elem = getElem(index);
if (nullptr == Elem)
{
return -1;
}
// 修改指针链
Elem->pProir->pNext = Elem->pNext;
Elem->pNext->pProir = Elem->pProir;
// 删除结点
delete Elem;
// 计数减一
num--;
return 0;
}
// 设定元素值
int Dlist::setValue(int index, int value)
{
DoubleNode* Elem = getElem(index);
if (nullptr == Elem)
{
return -1;
}
Elem->data = value;
return 0;
}
// 查找从Index 后面值为value的元素的索引
int Dlist::LocateElem(int index, int value)
{
DoubleNode* Elem = getElem(index);
if (nullptr == Elem)
{
return -1;
}
int retIndex = index;
do
{
if (Elem->data == value)
{
break;
}
retIndex++;
} while (nullptr != (Elem = Elem->pNext));
if (retIndex == num)
{
retIndex = -1;
}
// 函数值返回
return retIndex;
}
// 查找从Index 的值
int Dlist::GetElemValue(int index,int& value)
{
DoubleNode* Elem = getElem(index);
if (nullptr == Elem)
{
return -1;
}
value = Elem->data;
return 0;
}
// 判断链表是否为空
bool Dlist::IsEmpty()
{
return num == 0 ? true : false;
}
// 链表长度
int Dlist::Size()
{
return num;
}
KDqueue.h
#ifndef DATA_STRUCT_K_DQUEUE_H
#define DATA_STRUCT_K_DQUEUE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "Dlist.h"
/**
* 双端队列
*/
class KDqueue : public Dlist
{
public:
/**
* 构造函数
*/
KDqueue();
/**
* 析构函数
*/
virtual ~KDqueue();
/**
* 头插入
*/
int PushHead(int v);
/**
* 取得头元素
*/
int TopHead();
/**
* 删除头元素
*/
int PopHead();
/**
* 尾插入
*/
int PushTail(int v);
/**
* 取得尾元素
*/
int TopTail();
/**
* 弹出尾元素
*/
int PopTail();
/**
* 清空队列
*/
void clear();
KDqueue& operator=(const KDqueue& v);
// 打印数据
void PrintFromHead();
};
#endif
KDqueue.cpp
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KDqueue.h"
KDqueue::KDqueue() :Dlist()
{
}
KDqueue::~KDqueue()
{
}
int KDqueue::PushHead(int v)
{
int ret = InsertHead(v);
return ret;
}
int KDqueue::TopHead()
{
if (pTail == pHead->pNext)
{
return 0;
}
return pHead->pNext->data;
}
int KDqueue::PopHead()
{
DoubleNode* temp = pHead->pNext;
if (pTail == temp)
{
return -1;
}
num--;
pHead->pNext = temp->pNext;
temp->pNext->pProir = pHead;
delete temp;
return 0;
}
int KDqueue::PushTail(int v)
{
int ret = InsertEnd(v);
return ret;
}
int KDqueue::TopTail()
{
if (pHead == pTail->pProir)
{
return 0;
}
return pTail->pProir->data;
}
int KDqueue::PopTail()
{
DoubleNode* temp = pTail->pProir;
if (pHead == temp)
{
return -1;
}
num--;
pTail->pProir = temp->pProir;
temp->pProir->pNext = pTail;
delete temp;
return 0;
}
void KDqueue::clear()
{
while (pHead->pNext != pTail)
{
DoubleNode* Elem = pHead->pNext;
pHead->pNext = Elem->pNext;
delete Elem;
}
num = 0;
}
KDqueue& KDqueue::operator=(const KDqueue& v)
{
if (&v == this)
{
return *this;
}
this->clear();
if (v.pHead->pNext != v.pTail)
{
this->pHead->pNext = v.pHead->pNext;
v.pHead->pNext->pProir = this->pHead;
this->pTail->pProir = v.pTail->pProir;
v.pTail->pProir->pNext = this->pTail;
v.pHead->pNext = v.pTail;
v.pTail->pProir = v.pHead;
this->num = v.num;
}
return *this;
}
void KDqueue::PrintFromHead()
{
DoubleNode* Elem = pHead->pNext;
while (Elem != pTail)
{
cout << Elem->data << " ";
Elem = Elem->pNext;
}
cout << endl;
}
KQueue.h
#ifndef DATA_STRUCT_K_QUEUE_H
#define DATA_STRUCT_K_QUEUE_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KDqueue.h"
/**
* 队列实现类
*/
class KQueue : public KDqueue
{
public:
/**
* 构造函数
*/
KQueue();
/**
* 析构函数
*/
virtual ~KQueue();
/**
* 元素从队尾入队
*/
int Push(int v);
/**
* 取得队头元素
*/
int Top();
/**
* 弹出队头元素
*/
int Pop();
};
#endif
KQueue.cpp
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KQueue.h"
KQueue::KQueue()
{
}
KQueue::~KQueue()
{
}
int KQueue::Push(int v)
{
int ret = PushTail(v);
return ret;
}
int KQueue::Top()
{
int ret = TopHead();
return ret;
}
int KQueue::Pop()
{
int ret = PopHead();
return ret;
}
KStatck.h
#ifndef DATA_STRUCT_K_STATCK_H
#define DATA_STRUCT_K_STATCK_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KDqueue.h"
/**
* 栈实现类
*/
class KStatck : public KDqueue
{
public:
/**
* 栈构造函数
*/
KStatck();
/**
* 栈析构函数
*/
virtual ~KStatck();
/**
* 元素压栈
*/
int Push(int v);
/**
* 取得栈顶元素
*/
int Top();
/**
* 弹出栈顶元素
*/
int Pop();
};
#endif
KStatck.cpp
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KStatck.h"
KStatck::KStatck()
{
}
KStatck::~KStatck()
{
}
int KStatck::Push(int v)
{
int ret = PushHead(v);
return ret;
}
int KStatck::Top()
{
int ret = TopHead();
return ret;
}
int KStatck::Pop()
{
int ret = PopHead();
return ret;
}
KOperation.h
#ifndef DATA_STRUCT_K_OPERATION_H
#define DATA_STRUCT_K_OPERATION_H
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KStatck.h"
#include "KQueue.h"
/**
* 四则运算实现类
*/
class KOperation
{
private:
/**
* 栈对象,中缀转后缀,保存操作符,计算后缀,保存操作数
*/
KStatck m_oStatck;
/**
* 队列对象,保存式子结果值
*/
KQueue m_oQueue;
/**
* 最终计算的结果值
*/
int m_nResultValue;
public:
/**
* 构造函数
*/
KOperation();
/**
* 析构函数
*/
virtual ~KOperation();
/**
* 中缀转后缀
*/
int FromInToSuffix();
/**
* 计算后缀表达式
*/
int ClaculateSuffix();
/**
* 输出计算结果值
*/
void OutResult();
/**
* 输入字符串
*/
int InPutText(string strText);
};
#endif
KOperation.cpp
#include <string>
#include <vector>
#include <list>
#include <iostream>
#include <assert.h>
#include "KOperation.h"
enum op
{
Add_Enum = -100,
Sub_Enum,
Multi_Enum = -80,
divi_Enum,
LBrackets_Enum =-70,
RBrackets_Enum = -60
};
KOperation::KOperation()
{
}
KOperation::~KOperation()
{
}
int KOperation::FromInToSuffix()
{
KQueue QueueTemp;
while (!m_oQueue.IsEmpty())
{
m_oStatck.PrintFromHead();
int v = m_oQueue.Top();
m_oQueue.Pop();
if (v >= Add_Enum && v <= RBrackets_Enum)
{
// 左括号
if (v == LBrackets_Enum)
{
m_oStatck.Push(v);
continue;
}
// 右括号
if (v == RBrackets_Enum)
{
// 栈非空
if(!m_oStatck.IsEmpty())
{
int X = m_oStatck.Top();
m_oStatck.Pop();
if (X == LBrackets_Enum)
{
continue;
}
else
{
QueueTemp.Push(X);
bool flag = m_oStatck.IsEmpty();
if (flag)
{
return -1;
}
else
{
X = m_oStatck.Top();
m_oStatck.Pop();
if (X != LBrackets_Enum)
{
return -1;
}
}
}
}
else
{
return -1;
}
continue;
}
if (m_oStatck.IsEmpty())
{
m_oStatck.Push(v);
continue;
}
int X = m_oStatck.Top();
if (v > X+1)
{
QueueTemp.Push(v);
}
else
{
if (X == LBrackets_Enum)
{
m_oStatck.Push(v);
}
else
{
m_oStatck.Pop();
m_oStatck.Push(v);
QueueTemp.Push(X);
}
}
continue;
}
QueueTemp.Push(v);
}
// 栈空
while (!m_oStatck.IsEmpty())
{
int v = m_oStatck.Top();
m_oStatck.Pop();
if (v == LBrackets_Enum)
{
return -1;
}
QueueTemp.Push(v);
}
m_oQueue = QueueTemp;
m_oQueue.PrintFromHead();
return 0;
}
int KOperation::ClaculateSuffix()
{
m_oStatck.clear();
KQueue QueueTemp;
while (!m_oQueue.IsEmpty())
{
int v = m_oQueue.Top();
m_oQueue.Pop();
if (v >= Add_Enum && v <= RBrackets_Enum)
{
if (m_oStatck.Size() < 2)
{
return -1;
}
int R = m_oStatck.Top();
m_oStatck.Pop();
int L = m_oStatck.Top();
m_oStatck.Pop();
int ret = 0;
if (Add_Enum == v)
{
ret = L + R;
}
else if (Sub_Enum == v)
{
ret = L - R;
}
else if (Multi_Enum == v)
{
ret = L * R;
}
else if (divi_Enum == v)
{
ret = L / R;
}
m_oStatck.Push(ret);
continue;
}
m_oStatck.Push(v);
}
m_nResultValue = m_oStatck.Top();
m_oStatck.Pop();
return 0;
}
void KOperation::OutResult()
{
cout << "四则运算的结果为" << m_nResultValue << endl;
}
int KOperation::InPutText(string strText)
{
string temp;
for (auto v : strText)
{
if ((v >= '0' && v <= '9') || (v == '(') || (v == ')') || (v == '+') || (v == '-') || (v == '*') || (v == '/'))
{
if (v >= '0' && v <= '9')
{
temp.push_back(v);
}
else
{
if (!temp.empty())
{
m_oQueue.Push(atoi(temp.c_str()));
temp.clear();
}
switch (v)
{
case '+':
m_oQueue.Push(Add_Enum);
break;
case '-':
m_oQueue.Push(Sub_Enum);
break;
case '*':
m_oQueue.Push(Multi_Enum);
break;
case '/':
m_oQueue.Push(divi_Enum);
break;
case '(':
m_oQueue.Push(LBrackets_Enum);
break;
case ')':
m_oQueue.Push(RBrackets_Enum);
break;
default:
break;
}
}
}
else
{
return -1;
}
}
m_oQueue.PrintFromHead();
return 0;
}
结束




