[凸包] [旋转卡壳]凸包的构建与直径
[凸包][旋转卡壳]凸包的构建与直径
定义
用不严谨的话来讲:
给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点 ——百度百科
严谨的说法是这样的:
在一个实数向量空间\(V\)中,对于给定集合\(X\),所有包含\(X\)的凸集的交集\(S\)被称为\(X\)的凸包。 ——依然是百度百科
比如下面这些点:
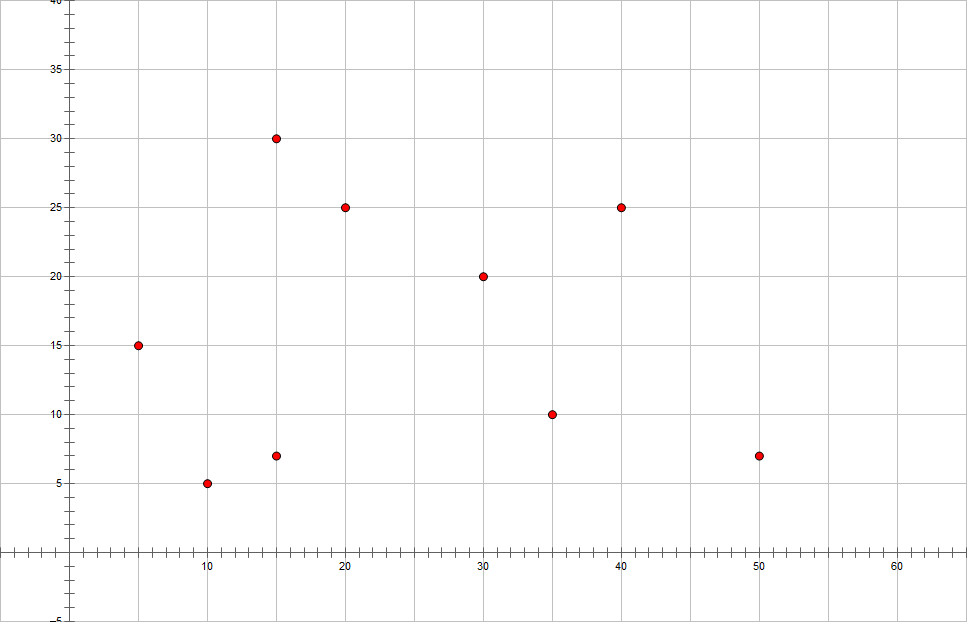
它们的凸包长这样:
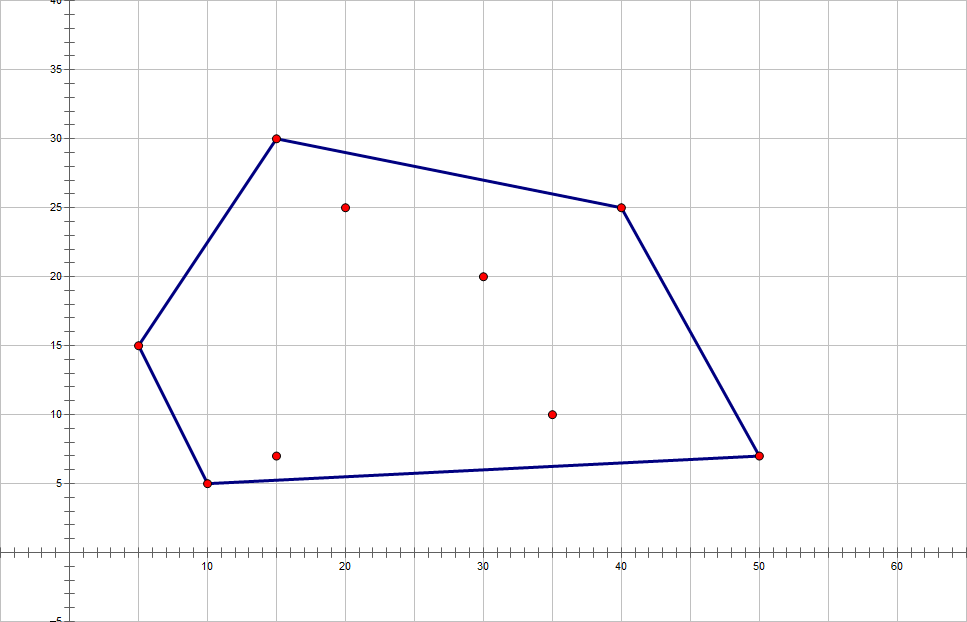
性质
凸包比较实用的性质我就发现了一个,以后如果有在补上
这个性质是:凸包的所有点都在凸包边的同一边,如图:
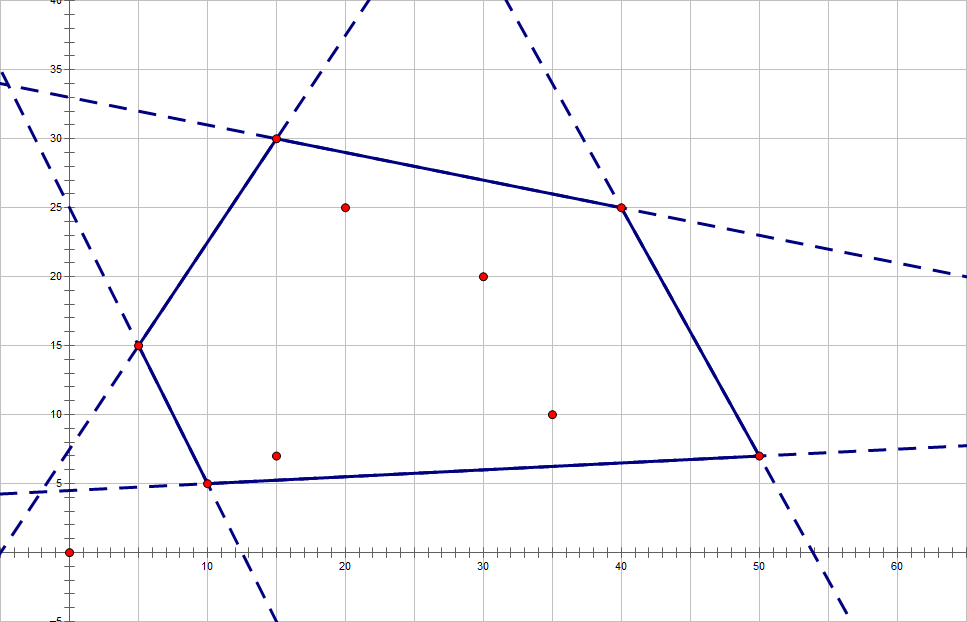
这对于我们构建凸包有用
构造
构建分为三步,找点,极角排序,连边
找出最下面的点,如果有两个或以上的这样的点,再在里面找最左边的点。
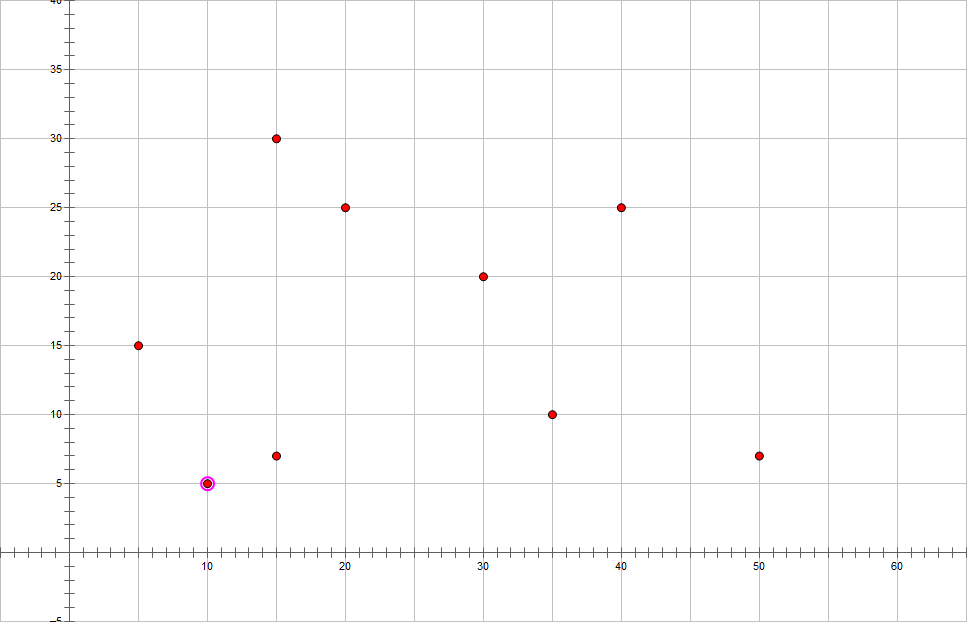
极角排序
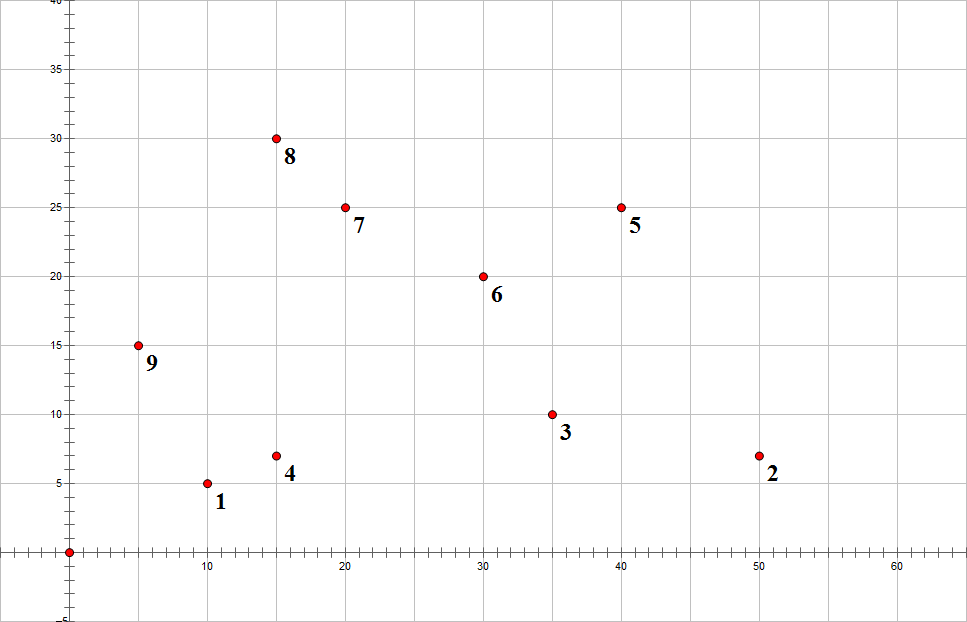
按顺序把点连起来,如果连的边是逆时针转的,那么就继续连,如果是顺时针的,那么就把现在这个点扔掉,用上一个点去连,直到是逆时针的。因为如果是顺时针转的,就会有点在上一条边的两边,不符合凸包的特性。
就像这样:
1连2

2连3

3连4
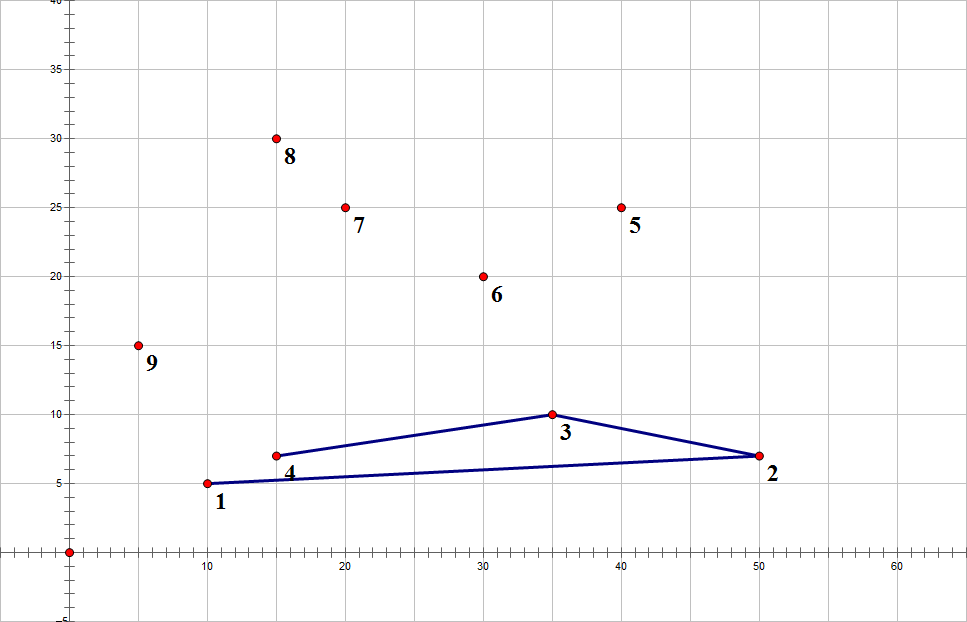
4连5

发现顺时针转了,去掉4,3连5

还是顺时针,去掉3,2连5
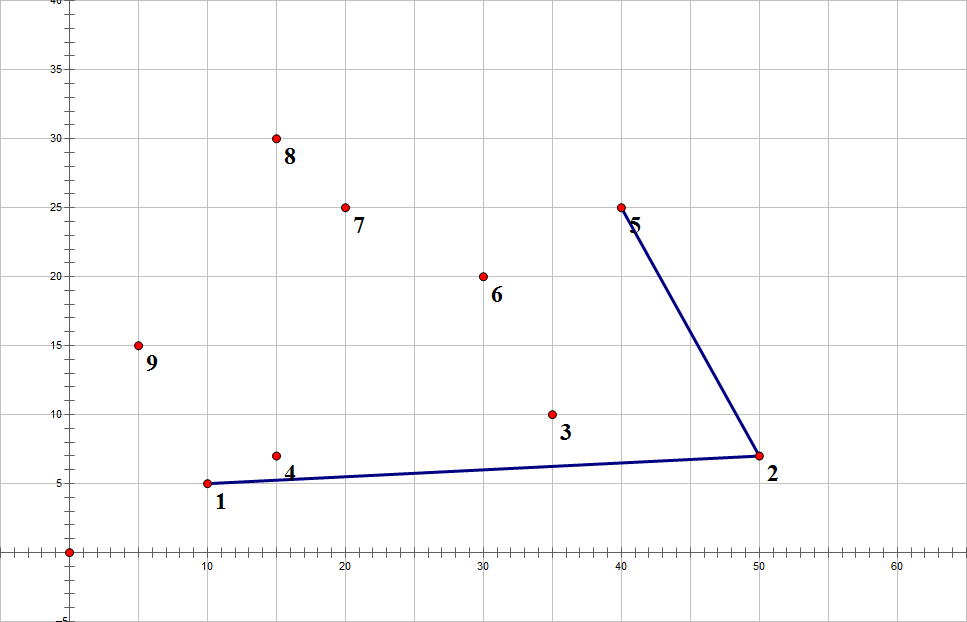
5连6
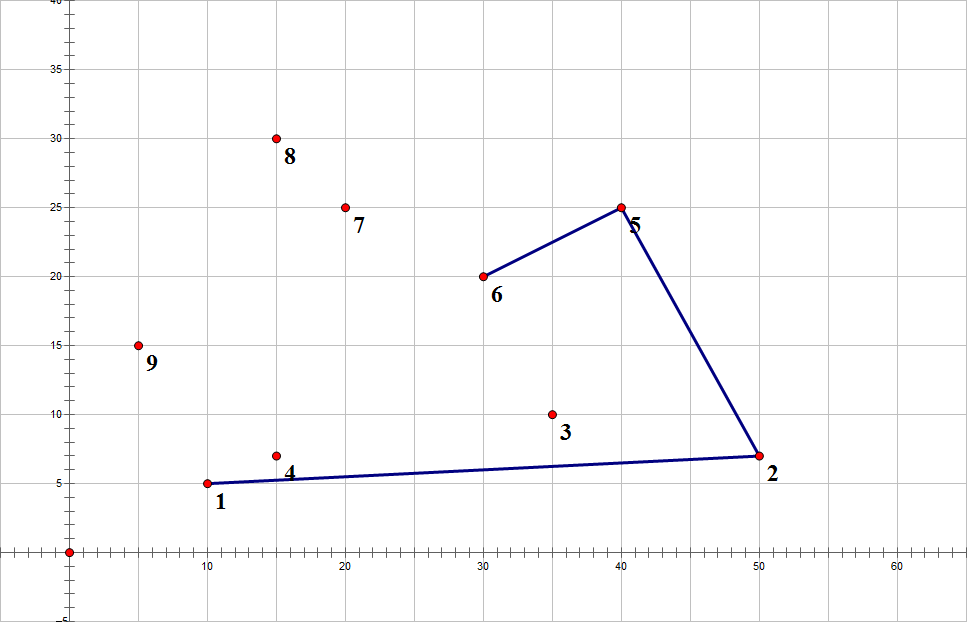
6连7
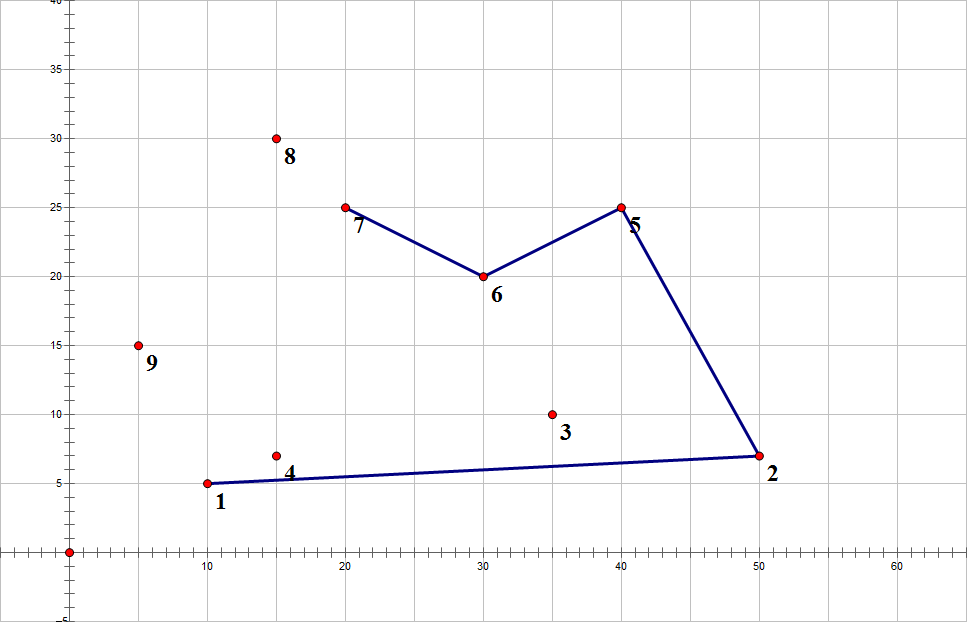
顺时针,去掉6,7连5

7连8

顺时针,去掉7,5连8
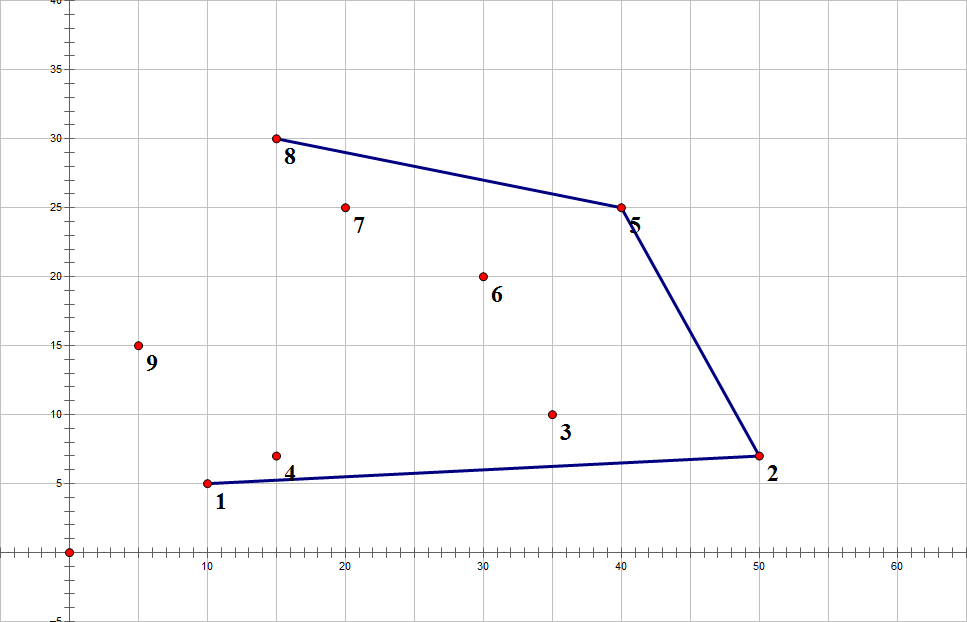
8连9
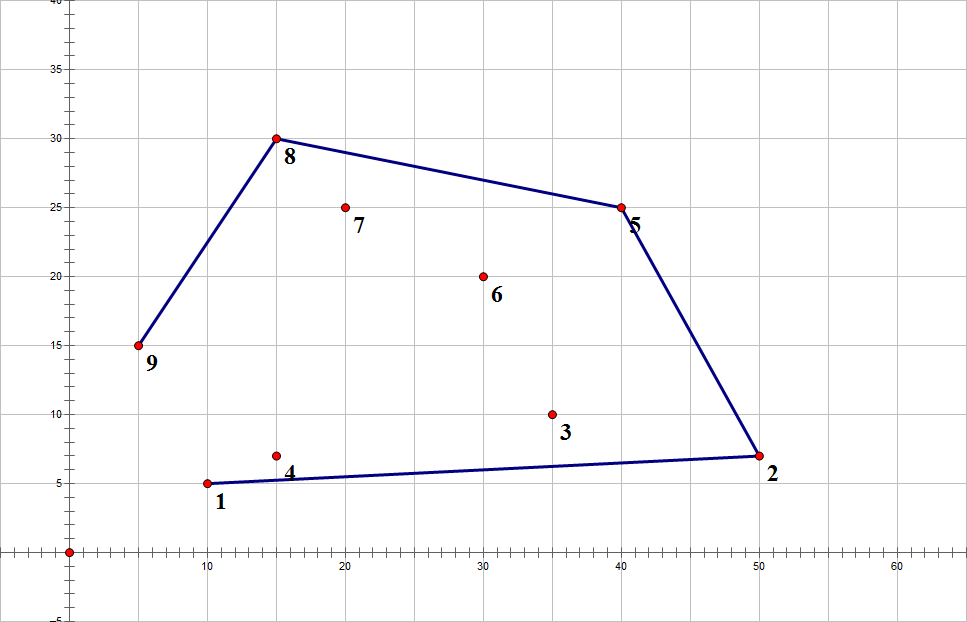
最后再把9连1

模板题:
裸的模板题,求凸包周长。
代码:
#include<bits/stdc++.h>
using namespace std;
const int MAXN=10001;
struct point{
double x,y;
point(double x_=0,double y_=0){
x=x_;
y=y_;
}
point friend operator-(point x,point y){
return point(x.x-y.x,x.y-y.y);
}
}p[MAXN],ans[MAXN];
int n;
double dis(point x,point y){
point tmp=x-y;
return sqrt(tmp.x*tmp.x+tmp.y*tmp.y);
}
double det(point x,point y){
return x.x*y.y-x.y*y.x;
}
bool cmp(point x,point y){
double tmp=det(x-p[1],y-p[1]);
if(tmp>0)
return true;
if(tmp==0&&dis(x,p[1])<dis(y,p[1]))
return true;
return false;
}
int get(point p[]){
int tmp=1;
for(int i=2;i<=n;i++)
if(p[i].y<p[tmp].y||(p[i].y==p[tmp].y&&p[i].x<=p[tmp].x))
tmp=i;
swap(p[1],p[tmp]);
sort(p+2,p+1+n,cmp);
ans[1]=p[1],ans[2]=p[2];
int siz=2;
for(int i=3;i<=n;i++){
while(siz>=2&&det(ans[siz]-ans[siz-1],p[i]-ans[siz-1])<=0)
siz--;
ans[++siz]=p[i];
}
return siz;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
int siz=get(p);
double ans_=dis(ans[1],ans[siz]);
for(int i=1;i<=siz-1;i++)
ans_=ans_+dis(ans[i],ans[i+1]);
printf("%.2f",ans_);
}
凸包的直径
就是凸包中离得最远的两个点之间的距离
大家都知道要用旋(xuan)转(zhuan)卡(qia)壳(qiao),我就讲一讲这个神奇暴力的算法
我们逆时针枚举每一条边,找出距离他们最远的点,那么直径可能是这个最远点到这条线段的两个端点其中一个点的距离

离1,2最远的是8
离2,5最远的是9
离5,8最远的是1
离8,9最远的是5
离9,1最远的是2
不难发现,最远的点也是逆时针出现的
所以我们可以逆时针枚举每一条边,记住离上一条边最远的点,从这个点继续逆时针枚举就好了
模板题:
就是凸包直径
代码:
#include<bits/stdc++.h>
using namespace std;
const long long MAXN=100001;
struct point{
long long x,y;
point(long long x_=0,long long y_=0){
x=x_;
y=y_;
}
point friend operator-(point a,point b){
return point(a.x-b.x,a.y-b.y);
}
}p[MAXN],ans[MAXN];
long long n,siz;
double dis(point x,point y){
point tmp=x-y;return sqrt(tmp.x*tmp.x+tmp.y*tmp.y);
}
double det(point x,point y){
return x.x*y.y-x.y*y.x;
}
bool cmp(point x,point y){
double tmp=det(x-p[1],y-p[1]);
if(tmp>0)
return true;
if(tmp==0&&dis(x,p[1])<dis(y,p[1]))
return true;
return false;
}
long long get(point p[],long long n){
long long tmp=1;
for(long long i=2;i<=n;i++)
if(p[i].y<p[tmp].y||(p[i].y==p[tmp].y&&p[i].x<=p[tmp].x))
tmp=i;
swap(p[1],p[tmp]);
sort(p+2,p+1+n,cmp);
ans[1]=p[1],ans[2]=p[2];
long long siz=2;
for(long long i=3;i<=n;i++){
while(siz>=2&&det(ans[siz]-ans[siz-1],p[i]-ans[siz-1])<=0)
siz--;
ans[++siz]=p[i];
}
return siz;
}
long long get_ans(point p[],long long n){
long long now=2,re=-1;
for(long long i=1;i<=n;i++){
long long nxt=(i==n)?(1):(i+1);
while(abs(det(p[now+1]-p[i],p[nxt]-p[i]))>abs(det(p[now]-p[i],p[nxt]-p[i]))){
now++;
if(now==n+1)
now=1;
}
point tmp_1=p[now]-p[i],tmp_2=p[now]-p[nxt];
re=max(re,max(tmp_1.x*tmp_1.x+tmp_1.y*tmp_1.y,tmp_2.x*tmp_2.x+tmp_2.y*tmp_2.y));
}
return re;
}
int main(){
scanf("%lld",&n);
for(long long i=1;i<=n;i++)
scanf("%lld%lld",&p[i].x,&p[i].y);
siz=get(p,n);
printf("%lld\n",get_ans(ans,siz));
}


