20162327 《程序设计与数据结构》第十一周学习总结
20162327 2017-2018-1 《程序设计与数据结构》第十一周学习总结
教材学习内容总结
- 1、在无向图中,表示边的顶点对是无序的
- 2、如果图中的两个顶点之间有边连接,则称它们是邻接的
- 3、如果无向图中的连接顶点的边数达到最大,则图为完全图
- 4、路径是图中连接顶点的边的序列
- 5、有向图中,边是顶点的有序对
- 6、有向图中的路径是连接两个顶点的有向边的序列
- 7、图的每条边上都有对应的权值的图称为带权图
- 8、图的深度优先遍历与广度优先遍历的主要差异在于栈代替队列来管理遍历过程
- 9、当且仅当从任意顶点开始的广度优先遍历中得到的顶点数等于图中所包含的顶点数时,图时连通
- 10、生成树时是包含图中所有顶点及图中部分边的一棵树
- 11、最小生成树是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树
教材学习中的问题和解决过程
- 问题1:图的遍历与树的遍历有什么区别?
- 问题1解决方案:树是有序的,图是无序的。图有两种林子里的方法,一种是广度优先遍历,另一种是深度优先遍历。对于树来说,它的广度优先遍历就是层序遍历,深度优先遍历就是先序遍历。
- 问题2:生成树和最小生成树的问题?
- 问题2解决方案: 解决最先生成树有两种算法,一种是Prim算法,这种算法是从点入手,适合比较稠密的图;另一种是Krukal算法,它是从边入手,适合于比较稀疏的图。
- 问题3:每一对顶点之间的最短路径问题?
- 问题3解决方案:第一种:Dijkstra算法——边上权值非负的情形的单源最短路径问题
第二种:Bellman-Ford——边上权值为任意值的单源最短路径问题
第三种:Floyd——所有顶点间的最短路径 - 问题3:附图列出某工程之间的优先关系和各工程所需时间,要求:
- 画出AOE网
- 列出各事件的最早、最迟发生时间
- 找出该AOE网中的关键路径,并回答完成该工程需要的最短时间
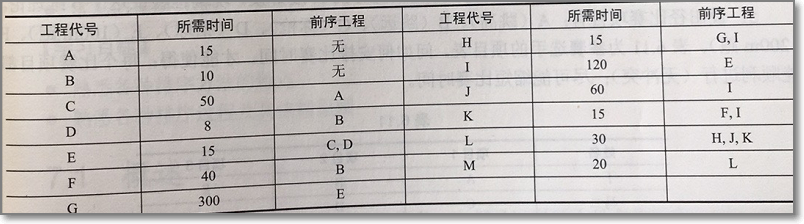
- 问题3解决方案:
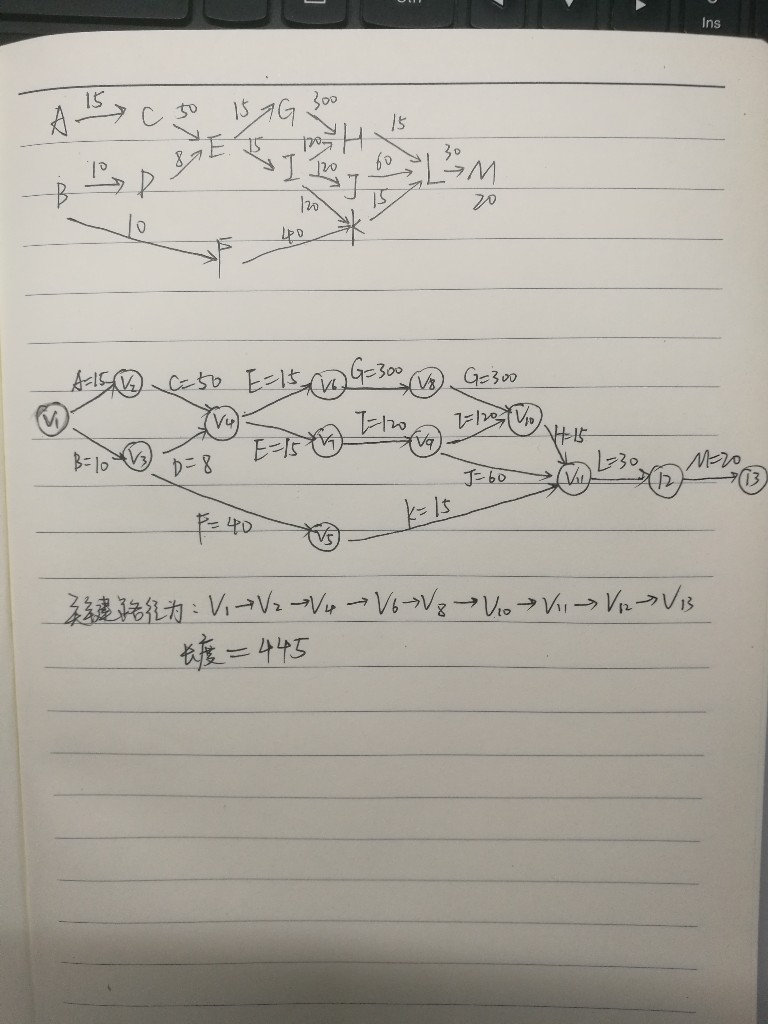
教材中出现的代码问题及解决过程
- 问题一:表示顶点集合的抽象图类
- 解决方案:
public abstract class AbstractGraph<T> //抽象图类
{
protected static final int MAX_WEIGHT=0x0000ffff; //∞
protected SeqList<T> vertexlist; //顶点顺序表
//构造空图,顶点数为0,length指定顶点顺序表容量
public AbstractGraph(int length)
public AbstractGraph()
public int vertexCount() //图的顶点数
public String toString() //图的顶点集合描述
public T getVertex(int i) //顶点元素
public void setVertex(int i, T x) //设置顶点元素为x
}
public abstract class AbstractGraph<T> //抽象图类
{
//以下抽象方法没有方法体,由子类提供实现
public abstract int insertVertex(T x); //插入顶点
public abstract void removeVertex(int i); //删除顶点及边
public abstract int weight(int i, int j); //边的权值
protected abstract int next(int i, int j); //后继邻接顶点
}
- 问题二:图带权值的边类
- 解决方案:
public class Triple implements Comparable<Triple>
{
int row, column, value; //行、列、元素
public int compareTo(Triple tri)
//按行、列位置比较大小,约定排序次序
}
- 问题三:邻接矩阵表示的带权图类
- 解决方案:
public class MatrixGraph<T>
extends AbstractGraph<T>
{
protected Matrix matrix; //存储图的邻接矩阵
public MatrixGraph(int length)
public MatrixGraph()
public MatrixGraph(T[] vertices)
public MatrixGraph(T[] vertices, Triple[] edges)
//顶点集和边集构造图
public String toString() //图的描述
}
代码托管
本周结对学习情况
其他
- 数据结构现在应该学的比较完整了,感觉图是对前几个数据结构的一个综合运用,该下功夫整理整理了。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 300/500 | 2/4 | 18/38 | |
| 第三周 | 500/1000 | 3/7 | 22/60 | |
| 第四周 | 300/1300 | 2/9 | 30/90 |
参考:软件工程软件的估计为什么这么难,软件工程 估计方法
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)


