信息安全系统设计基础第四周学习内容

     我们对计算机系统的探索是从学习计算机本身开始的，它由处理器和
存储器子系统组成。在核心部分，我们需要方法来表示基本数据类型，比
如整数和实数运算的近似值。然后，我们考虑机器级指令如何操作这样的 数据，以及编译器如何将 C 程序翻译成这样的指令。接下来，研究几种实
现处理器的方法，帮助我们更好地了解硬件资源是如何被用来执行指令。 一旦理解了编译器和机器级代码，我们就能通过编写最高性能的 C 程序，
来分析如何最大化程序的性能。

   二进制的历史

       现代计算机存储和处理的信息以二值信号表示。这些微不足道的二进制数字，或者称为位 （bit），奠定了数字革命的基础。大家熟悉并且使用了 1000 多年的十进制（以十为基数）起源于 印度，12 世纪被阿拉伯数学家改进，并在 13 世纪被意大利数学家 Leonardo Pisano（公元 11701250，更为大家所熟知的名字是 Fibonacci）带到西方。对于有 10 个手指的人类来说，使用十进 制表示法是很自然的事情，但是当构造存储和处理信息的机器时，二进制的值工作得更好。二值 信号能够很容易地被表示、存储和传输，例如，可以表示为穿孔卡片上有洞或无洞、导线上的电压或低电压，或者顺时针或逆时针的磁场。对二值信号进行存储和执行计算的电子电路非常简 单和可靠，制造商能够在一个单独的硅片上集成数百万甚至数十亿个这样的电路。

三种数字表示

         无符号（unsigned）编码基于传统的二进制表示法，表示 大于或者等于零的数字。补码（two’s-complement）编码是表示有符号整数的最常见的方式，有 符号整数就是可以为正或者为负的数字。浮点数（floating-point）编码是表示实数的科学记数法 的以二为基数的版本。

 溢出（overflow）的例子：

     现在的大多数计算机 （使用 32 位来表示数据类型int），计算表达式200*300*400*500会得出结果 -884 901 888。 这违背了整数运算的特性，计算一组正数的乘积不应产生一个为负的结果。

 整数的计算机运算满足人们所熟知的真正整数运算的定律。

利用乘法的结 合律和交换律，计算下面任何一个 C 表达式，都会得出结果 -884 901 888 ： (500*400)*(300*200) ((500*400)*300)*200 ((200*500)*300)*400 400*(200*(300*500))
计算机可能没有产生期望的结果，但是至少结果是一致的！

C 编程语言的演变

                 前面提到过，C 编程语言是贝尔实验室的 Dennis Ritchie 最早开发出来的，目的是和 Unix 操 作系统一起使用（Unix 也是贝尔实验室开发的）。在那个时候，大多数系统程序，例如操作系 统，为了访问不同数据类型的低级表示，都必须用大量的汇编代码编写。比如说，像malloc 库函数提供的内存分配那样的功能，用当时的其他高级语言是无法编写的。

信息存储

      大多数计算机使用8位的块，或者字节（byte），作为 最小的可寻址的存储器单位，而不是在存储器中访问单独 的位。机器级程序将存储器视为一个非常大的字节数组， 称为虚拟存储器（virtual memory）。存储器的每个字节都由 一个唯一的数字来标识，称为它的地址（address），所有可 能地址的集合称为虚拟地址空间（virtual address space）。顾 名思义，这个虚拟地址空间只是一个展现给机器级程序的 概念性映像。实际的实现（见第9章）是将随机访问存储器（RAM）、磁盘存储器、特殊硬件和操作 系统软件结合起来，为程序提供一个看上去统一的字节数组。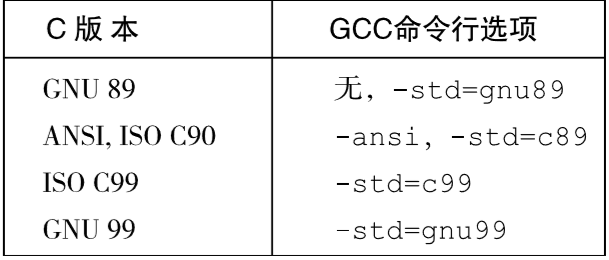

 

十六进制表示法

      一个字节由 8 位组成。在二进制表示法中，它的值域是 000000002 ～ 111111112 ；如果用十 进制整数表示，它的值域就是 010 ～ 25510。两种表示法对于描述位模式来说都不是非常方便。二 进制表示法太冗长，而十进制表示法与位模式的互相转化又很麻烦。替代的方法是，以 16 为基 数，或者叫十六进制（hexadecimal）数，来表示位模式。十六进制（简写为“hex”）使用数字 ‘0’～‘9’，以及字符‘A’～‘F’来表示 16 个可能的值。图 2-2 展示了 16 个十六进制数字 对应的十进制值和二进制值。用十六进制书写，一个字节的值域为 0016 ～ FF16。

         比如，假设给你一个数字0x173A4C，可以通过展开每个十六进制数字，将它转换为二进 制格式，如下所示 ： 十六进制    1   7  3  A  4  C 二进制 0001 0111 0011 1010 0100 1100 这样就得到了二进制表示000101110011101001001100。 反过来，如果给定一个二进制数字 1111001010110110110011，你可以首先把它分为每 4 位一 组，再把它转换为十六进制。不过要注意，如果位的总数不是 4 的倍数，最左边的一组可以少于 4 位，前面用 0 补足，然后将每个 4 位组转换为相应的十六进制数字 ： 二进制 11 1100 1010 1101 1011 0011 十六进制  3  C  A  D  B  3

十进制和十六进制表示之间的转换

          将一个十进制数 字 x 转换为十六进制，可以反复地用 16 除 x，得到一个商 q 和一个余数 r，也就是 x = q×16 + r。 然后，我们用十六进制数字表示的 r 作为最低位数字，并且通过对 q 反复进行这个过程得到剩下 的数字。例如，考虑十进制 314156 的转换 ： 314156  =  19634×16 + 12　　（C） 19634  =  1227×16 + 2 　　　（ 2） 1227  =  76×16 + 11　  　　（B） 76  =  4×16 + 12    　　　（C） 4  =  0×16 + 4          　　 （4） 从这里，我们能读出十六进制表示为0x4CB2C。 反过来，将一个十六进制数字转换为十进制数字，我们可以用相应的 16 的幂乘以每个十六 进制数字。比如，给定数字0x7AF，我们计算它对应的十进制值为 7×162 + 10×16 + 15=7×256 +  10×16+15=1792+160+15=1967。

字

       每台计算机都有一个字长（word size），指明整数和指针数据的标称大小（nominal size）。因 为虚拟地址是以这样的一个字来编码的，所以字长决定的最重要的系统参数就是虚拟地址空间的 最大大小。也就是说，对于一个字长为 w 位的机器而言，虚拟地址的范围为 0 ～ 2w-1，程序最多 访问 2w 个字节。

数据大小

       

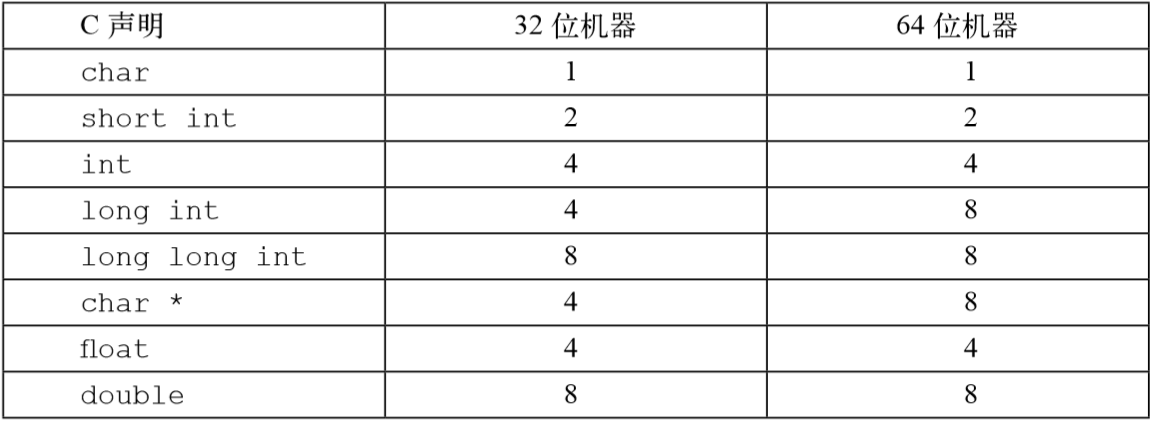
计算机和编译器支持多种不同方式编码的数字格式，如整数和浮点数，以及其他长度的数 字。比如，许多机器都有处理单个字节的指令，也有处理表示为 2 字节、4 字节或者 8 字节整数 的指令，还有些指令支持表示为 4 字节和 8 字节的浮点数。 C 语言支持整数和浮点数的多种数据格式。C 的数据类型char表示一个单独的字节。尽管 “char”是由于它被用来存储文本串中的单个字符这一事实而得名，但它也能用来存储整数值。 C 的数据类型int之前还能加上限定词short、long，以及最近的long long，以提供各种 大小的整数表示

寻址和字节顺序

    对于跨越多字节的程序对象，我们必须建立两个规则 ：这个对象的地址是什么，以及在存 储器中如何排列这些字节。在几乎所有的机器上，多字节对象都被存储为连续的字节序列，对 象的地址为所使用字节中最小的地址。例如，假设一个类型为int的变量x的地址为0x100， 也就是说，地址表达式&x的值为0x100。那么，x的 4 个字节将被存储在存储器的0x100、 0x101、0x102和0x103位置。某些机器选择在存储器中按照从最低有效字节到最高 有效字节的顺序存储对象，而另一些机器则按照从最高有效字节到最低有效字节的顺序存储。前 一种规则—最低有效字节在最前面的方式，称为小端法（little endian）。大多数 Intel 兼容机都 采用这种规则。后一种规则—最高有效字节在最前面的方式，称为大端法（big endian）。大多 数 IBM 和 Sun Microsystems 的机器都采用这种规则。注意我们说的是“大多数”。这些规则并没 有严格按照企业界限来划分。比如，IBM 和 Sun 制造的个人计算机使用的是 Intel 兼容的处理器， 因此用的就是小端法。许多比较新的微处理器使用双端法（bi-endian），也就是说可以把它们配 置成作为大端或者小端的机器运行。

    字节顺序变得可见的第三种情况是当编写规避正常的类型系统的程序时。在 C 语言中，可 以使用强制类型转换（cast）来允许以一种数据类型引用一个对象，而这种数据类型与创建这个 对象时定义的数据类型不同。大多数应用编程都强烈不推荐这种编码技巧，但是它们对系统级编 程来说是非常有用，甚至是必需的。

给 C 语言初学者 ：使用typedef命名数据类型：

C 语言中的typedef声明提供了一种给数据类型命名的方式。这能够极大地改善代码的可 读性，因为深度嵌套的类型声明很难读懂。

给 C 语言初学者 ：使用printf格式化输出：

printf函数（还有它的同类fprintf和sprintf）提供了一种打印信息的方式，这种 方式对格式化细节有相当大的控制能力。第一个参数是格式串（format string），而其余的 参数都是要打印的值。在格式串里，每个以'%'开始的字符序列都表示如何格式化下一个参数。 典型的示例有 ：'%d'是输出一个十进制整数，'%f'是输出一个浮点数，而'%c'是输出一个 字符，其编码由参数给出。

给 C 语言初学者 ：指针和数组

在函数show_bytes（图 2-4）中，我们看到指针和数组之间紧密的联系，这将在 3.8 节中 详细描述。这个函数有一个类型为byte_pointer（被定义为一个指向unsigned char的 指针）的参数start，但是我们在第 8 行上看到数组引用start[i]。在 C 语言中，我们能够 用数组表示法来引用指针，同时我们也能用指针表示法来引用数组元素。在这个例子中，引用 start[i]表示我们想要读取以start指向的位置为起始的第i个位置处的字节。

给 C 语言初学者 ：指针的创建和间接引用

我们看到对 C 和 C++ 中两种独有操作的使用。C 的“取地址” 运算符&创建一个指针。在这三行中，表达式&x创建了一个指向保存变量x的位置的指针。这 个指针的类型取决于x的类型，因此这三个指针的类型分别为int*、float*和void**。（数 据类型void*是一种特殊类型的指针，没有相关联的类型信息。） 强制类型转换运算符可以将一种数据类型转换为另一种。因此，强制类型转换（byte_ pointer）&x表明无论指针&x以前是什么类型，它现在就是一个指向数据类型为unsigned char的指针。这里给出的这些强制类型转换不会改变真实的指针，它们只是告诉编译器以新的 数据类型来看待被指向的数据。

Linux 32 ：运行 Linux 的 Intel IA32 处理器

Windows ：运行 Windows 的 Intel IA32

Sun ：          运行 Solaris 的 Sun Microsystems SPARC 处理器

Linux 64 ：运行 Linux 的 Intel x86-64 处理器

布尔代数简介

    二进制值是计算机编码、存储和操作信息的核心，所以围绕数值 0 和 1 的研究已经演化出了 丰富的数学知识体系。这起源于 1850 年前后乔治 • 布尔（George Boole，1815—1864）的工作， 因此也称为布尔代数（Bool algebra）。布尔注意到通过将逻辑值 TRUE（真）和 FALSE（假）编 码为二进制值 1 和 0，能够设计出一种代数，以研究逻辑推理的基本原则。 最简单的布尔代数是在二元集合 {0，1} 基础上的定义。图 2-7 定义了这种布尔代数中的几 种运算。我们用来表示这些运算的符号是和 C 语言的位级运算使用的符号相匹配的，这些将在 后面讨论到。布尔运算 ~ 对应于逻辑运算 NOT，在命题逻辑中用符号﹁表示。也就是说，当 P 不是真的时候，我们就说﹁ P 是真的，反之亦然。相应地，当 P 等于 0 时，~P 等于 1，反之亦 然。布尔运算 &对应于逻辑运算AND，在命题逻辑中用符号∧表示。当P和Q都为真时，我们说 P∧Q为真。相应地，只有当p =1且q =1时，p & q才等于1。布尔运算｜对应于逻辑运算OR，在 命题逻辑中用符号∨表示。当P或者Q为真时，我们说P∨Q成立。相应地，当p =1或者q =1时， p｜q等于1。布尔运算^对应于逻辑运算异或，在命题逻辑中用符号σ表示。当P或者Q为真但 不同时为真时，我们说PσQ成立。相应地，当p =1且q =0，或者p =0且q =1时，p^q等于1。

C 语言中的位级运算

C 语言的一个很有用的特性就是它支持按位布尔运算。事实上，我们在布尔运算中使用的那 些符号就是 C 语言所使用的 ： | 就是 OR（或），& 就是 AND（与），~ 就是 NOT（取反），而 ^ 就 是 EXCLUSIVE-OR（异或）。这些运算能运用到任何“整型”的数据类型上，也就是那些声明为 char或者int的数据类型，无论它们有没有像short、long、long long或者unsigned 这样的限定词。

 

整数表示

在本节中，我们描述用位来编码整数的两种不同的方式 ：一种只能表示非负数，而另一种能 够表示负数、零和正数。后面我们将会看到它们的数学属性和机器级实现方面密切关联。我们还 会研究扩展或者收缩一个已编码整数以适应不同长度表示的效果。

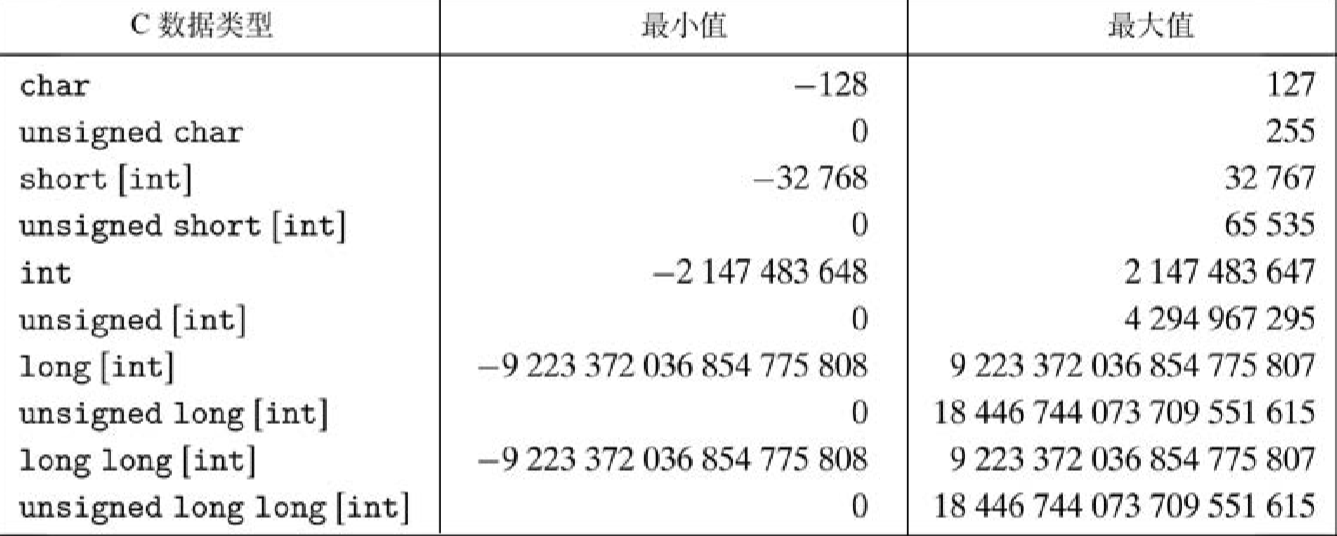
        C 语言支持多种整型数据类型—表示有限范围的整数。这些类型如图 2-8 和图 2-9 所示， 其中还给出了“典型的”32 位和 64 位机器的取值范围。每种类型都能用关键字来指定大小，这 些关键字包括char、short、long或者long long，同时还可以指示被表示的数字是非负 数（声明为unsigned），或者可能是负数（默认）。如图 2-3 所示，这些不同大小的分配的字节 数会根据机器的字长和编译器有所不同。根据字节分配，不同的大小所能表示的值的范围是不同 的。这里给出来的唯一一个与机器相关的取值范围是大小指示符long的。大多数 64 位机器使 用 8 个字节表示，比 32 位机器上使用的 4 个字节表示的取值范围大很多。

 

     C 语言标准定义了每种数据类型必须能够表示的最小的取值范围。如图 2-10 所示，它们 的取值范围与图 2-8 和图 2-9 所示的典型实现一样或者小一些。特别地，我们看到它们只要 求正数和负数的取值范围是对称的。此外，数据类型 int 可以用 2 个字节的数字来实现，而 这几乎退回到了 16 位机器的时代。还看到，long 的大小可以用 4 个字节的数字来实现，而 实际上也常常是这样。数据类型 long long 是在 ISO C99 中引入的，它需要至少 8 个字节 表示。

无符号数的编码

假设一个整数数据类型有 w 位。我们可以将位向量写成 x →，表示整个向量，或者写成 [xw-1 ， xw-2，…，x0]，表示向量中的每一位。把 x → 看做一个二进制表示的数，就获得了 x → 的无符号表示。 我们用一个函数 B2Uw（Binary to Unsigned）的缩写，长度为 w）来表示 ：
B2Uw(� x)
. =
w−1 � i=0
xi2i
                           　　　　　　　　　　 （2-1）
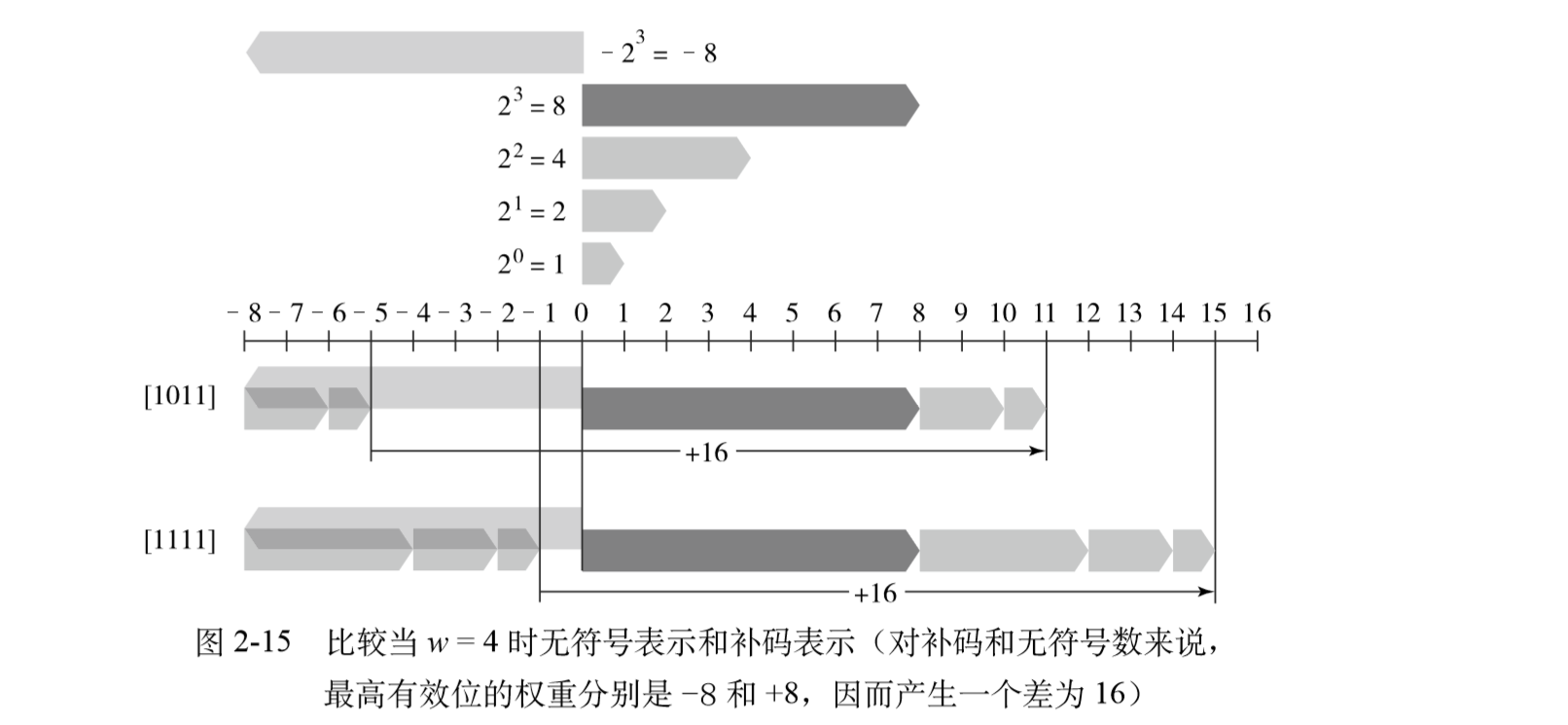
在这个等式中，符号“＝ 4 ”表示左边被定义为等于右边。函数B2Uw 将一个长度为w的0、1串映射 到非负整数。举一个示例，图2-11展示的是下面几种情况下B2U给出的从位向量到整数的映射。 B2U4([0001]) = 0 . 23+0 . 22+0 . 21+1. 20 = 0+0+0+1 = 1 B2U4([0101]) = 0 . 23+1. 22+0 . 21+1. 20 = 0+4+0+1 = 5 B2U4([1011]) = 1. 23+0 . 22+1. 21+1. 20 = 8+0+2+1 = 11 B2U4([1111]) = 1. 23+1. 22+1. 21+1. 20 = 8+4+2+1 = 15 　　 （2-2）

在图中，我们用长度为 2i 的指向右侧箭头的条表示每个位的位置 i。每个位向量对应的数值

补码编码

对于许多应用，我们还希望表示负数值。最常见的有符号数的计算机表示方式就是补码 （two’s-complement）形式。在这个定义中，将字的最高有效位解释为负权（negative weight）。 我们用函数 B2Tw（Binary to Two’s-complement 的缩写，长度为 w）来表示 ： B2Tw(� x) . =−xw−12w−1+ w−2 � i=0 xi2i 　　　　　　　　　　　（2-3） 最高有效位 xw-1 也称为符号位，它的“权重”为 -2w-1，是无符号表示中权重的负数。符号 位被设置为 1 时，表示值为负，而当设置为 0 时，值为非负。这里来看一个示例，图 2-12 展示 的是下面几种情况下 B2T 给出的从位向量到整数的映射。 　 （2-4）
在这个图中，我们用向左指的条表示符号位具有负权重。于是，与一个位向量相关联的数值 是由可能的向左指的灰色条和向右指的蓝色条加起来决定的。
＝ 4
正文.indd   39 2010-10-19   14:18:15
　 4 0 　　 第 一 部 分 　 程 序 结 构 和 执 行 　
就等于所有值为 1 的位对应的条的长度之和。

有符号数的其他表示方法 有符号数还有两种标准的表示方法 ： 反码（Ones’ Complement）：除了最高有效位的权是 -(2w-1-1) 而不是 -2w-1，它和补码是一 样的 ：
原码（Sign-Magnitude）：最高有效位是符号位，用来确定剩下的位应该取负权还是正权 ：
这两种表示方法都有一个奇怪的属性，那就是对于数字 0 有两种不同的编码方式。这两种表 示方法，把 [00…0] 都解释为 +0。而值 -0 在原码中表示为 [10…0]，在反码中表示为 [11…1]。 虽然过去生产过基于反码表示的机器，但是几乎所有的现代机器都使用补码。我们将看到在浮点 数中有使用原码编码。 请注意补码（Two’s complement）和反码（Ones’complement）中撇号的位置是不同的。术语 补码来源于这样一个情况，对于非负数 x，我们用 2w-x（这里只有一个 2）来计算 -x 的 w 位表示。 术语反码来源于这样一个属性，我们用 [111...1] -x（这里有很多个 1）来计算 -x 的反码表示。

有符号数和无符号数之间的转换

C 语言允许在各种不同的数字数据类型之间做强制类型转换。例如，假设变量x声明为 int，u声明为unsigned。表达式(unsigned)x会将x的值转换成一个无符号数值，而 (int)u将u的值转换成一个有符号整数。将有符号数强制类型转换成无符号数，或者反过来， 会得到什么结果呢？从数学的角度来说，可以想象到几种不同的规则。很明显，对于在两种形式 中都能表示的值，我们是想要保持不变的。另一方面，将负数转换成无符号数可能会得到 0。如 果转换的无符号数太大以至于超出了补码能够表示的范围，可能会得到 TMax。不过，对于大多 数 C 语言的实现来说，对这个问题的回答都是从位级角度来看的，而不是数的角度。

C 语言中的有符号数与无符号数

如图 2-8 和图 2-9 所示，C 语言支持所有整型数据类型的有符号和无符号运算。尽管 C 语言 标准没有指定有符号数要采用某种表示，但是几乎所有的机器都使用补码。通常，大多数数字都 默认为是有符号的。例如，当声明一个像12345或者0x1A2B这样的常量时，这个值就被认为 是有符号的。要创建一个无符号常量，必须加上后缀字符‘U’或者‘u’。例如，12345U或者 0x1A2Bu。 C 语言允许无符号数和有符号数之间的转换。转换的原则是底层的位表示保持不变。因此， 在一台采用补码的机器上，当从无符号数转换为有符号数时，效果就是应用函数 U2Tw，而从有 符号数转换为无符号数时，就是应用函数 T2Uw，其中 w 表示数据类型的位数。 显式的强制类型转换就会导致转换发生，就像下面的代码 ：
1 int tx, ty; 2 unsigned ux, uy; 3 4 tx = (int) ux; 5 uy = (unsigned) ty;
另外，当一种类型的表达式被赋值给另外一种类型的变量时，转换是隐式发生的，就像下面 的代码 ：
1 int tx, ty; 2 unsigned ux, uy; 3 4 tx = ux; /* Cast to signed */ 5 uy = ty; /* Cast to unsigned */ 当用printf输出数值时，分别用指示符%d、%u和%x以有符号十进制、无符号十进制和 十六进制格式输出一个数字。注意printf没有使用任何类型信息，所以它可以用指示符%u来 输出类型为int的数值，也可以用指示符%d输出类型为unsigned的数值。例如，考虑下面 的代码 ：
1 int x = -1; 2 unsignedu=2147483648; /* 2 to the 31st */ 3 4 printf("x = %u = %d\n", x, x); 5 printf("u = %u = %d\n", u, u);
正文.indd   47 2010-10-19   14:18:20
　 4 8 　　 第 一 部 分 　 程 序 结 构 和 执 行 　
当在一个 32 位机器上运行时，它的输出如下 ： x = 4294967295 = -1 u = 2147483648 = -2147483648 在这两种情况下，printf首先将这个字当作一个无符号数输出，然后把它当作一个有符号 数输出。以下是实际运行中的转换函数 ：T2U32(-1) = UMax32 = 232-1 和 U2T32(231) = 231 - 232 = - 231 = TMin32。

扩展一个数字的位表示

一种常见的运算是在不同字长的整数之间转换，同时又保持数值不变。当然，当目标数据类 型太小以至于不能表示想要的值时，这根本就是不可能的。然而，从一个较小的数据类型转换 到一个较大的类型，这应该总是可能的。将一个无符号数转换为一个更大的数据类型，我们只 需要简单地在表示的开头添加 0，这种运算称为零扩展（zero extension）。将一个补码数字转换 为一个更大的数据类型可以执行符号扩展（sign extension），规则是在表示中添加最高有效位的 值的副本。由此可知，如果我们原始值的位表示为 [xw-1，xw-2，…，x0]，那么扩展后的表示就为 [xw-1，…，xw-1，xw-1，xw-2，…，x0]。（我们用浅灰色标出符号位 xw-1 来突出它们在符号扩展中的 角色。） 例如，考虑下面的代码 ：
1 short sx = -12345; /* -12345 */ 2 unsigned short usx = sx; /* 53191 */ 3 int x = sx; /* -12345 */ 4 unsigned ux = usx; /* 53191 */ 5 6 printf("sx = %d:\t", sx); 7 show_bytes((byte_pointer) &sx, sizeof(short)); 8 printf("usx = %u:\t", usx); 9 show_bytes((byte_pointer) &usx, sizeof(unsigned short)); 10 printf("x = %d:\t", x); 11 show_bytes((byte_pointer) &x, sizeof(int)); 12 printf("ux = %u:\t", ux); 13 show_bytes((byte_pointer) &ux, sizeof(unsigned));
在采用补码表示的 32 位大端法机器上运行这段代码时，打印出如下输出 ：
sx = -12345: cf c7 usx = 53191: cf c7 x = -12345: ff ff cf c7 ux = 53191: 00 00 cf c7
我们看到，尽管-12 345 的补码表示和 53 191 的无符号表示在 16 位字长时是相同的，但是在 32 位字长时却是不同的。特别地，-12 345 的十六进制表示为0xFFFFCFC7，而 53 191 的十六进 制表示为0x0000CFC7。前者使用的是符号扩展—最开头加了 16 位，都是最高有效位 1，表示 为十六进制就是0xFFFF。后者开头使用 16 个 0 来扩展，表示为十六进制就是0x0000。

截断数字

假设我们不用额外的位来扩展一个数值，而是减少表示一个数字的位数。例如下面代码中这 种情况 ：
1 int x = 53191; 2 short sx = (short) x; /* -12345 */ 3 int y = sx; /* -12345 */
在一台典型的 32 位机器上，当把 x 强制类型转换为short时，我们就将 32 位的int截断 为 16 位的short int。就像前面所看到的，这个 16 位的位模式就是 -12 345 的补码表示。当 我们把它强制类型转换回int时，符号扩展把高 16 位设置为 1，从而生成 -12 345 的 32 位补码 表关于有符号数与无符号数的建议 就像我们看到的那样，有符号数到无符号数的隐式强制类型转换导致了某些非直观的行为。而 这些非直观的特性经常导致程序错误，并且这种包含隐式强制类型转换细微差别的错误很难被发现。 因为这种强制类型转换是在代码中没有明确指示的情况下发生的，程序员经常忽视了它的影响。 下面两个练习题说明了某些由于隐式强制类型转换和无符号数据类型造成的细微错误。  练习题 2.25　考虑下列代码，这段代码试图计算数组a中所有元素的和，其中元素的数量由参数length给出。
1 /* WARNING: This is buggy code */ 2 float sum_elements(float a[], unsigned length) { 3 int i; 4 float result = 0; 5 6 for (i = 0; i <= length-1; i++) 7 result += a[i]; 8 return result; 9 } 　　当参数length等于0时，运行这段代码应该返回0.0。但实际上，运行时会遇到一个存储器错误。 请解释为什么会发生这样的情况，并且说明如何修改代码。
B2Uw([xw−1,xw−2,...,x 0]) mod2k =�w−1 � i=0
xi2i�mod2k
=�k−1 � i=0
xi2i�mod2k
=
k−1 � i=0
xi2i
=B2Uk([xk−1,x k−2,...,x 0]) ≤
正文.indd   52 2010-10-19   14:18:22
　 　 5 3 　
　现在给你一个任务，写一个函数用来判定一个字符串是否比另一个更长。前提是你要用 字符串库函数strlen，它的声明如下 ：
/* Prototype for library function strlen */ size_t strlen(const char *s);
最开始你写的函数是这样的 ：
/* Determine whether string s is longer than string t */ /* WARNING: This function is buggy */ int strlonger(char *s, char *t) { return strlen(s) - strlen(t) > 0; } 当你在一些示例数据上测试这个函数时，一切似乎都是正确的。进一步研究发现在头文件stdio.h 中数据类型size_t是定义成unsigned int的。 A. 在什么情况下，这个函数会产生不正确的结果？ B. 解释为什么会出现这样不正确的结果。 C. 说明如何修改这段代码好让它能可靠地工作。

整数运算

  许多刚入门的程序员非常惊奇地发现，两个正数相加会得出一个负数，并且比较表达式x<y 和比较表达式x-y<0会产生不同的结果。这些属性是由于计算机运算的有限性造成的。理解计 算机运算的细微之处能够帮助程序员编写更可靠的代码。

无符号乘法

范围在 0≤x, y≤ 2w-1 内的整数 x 和 y 可以表示为 w 位的无符号数，但是它们的乘积 x · y 的取值范围为 0 到 (2w-1)2 = 22w-2w+1+1 之间。这可能需要 2w 位来表示。不过，C 语言中的无符 号乘法被定义为产生 w 位的值，就是 2w 位的整数乘积的低 w 位表示的值。根据等式（2-9），这 可以看作等价于计算乘积模 2w。因此，w 位无符号乘法运算 *  w u 的结果为 ： x *  w u y ＝ (x·y) mod 2w     

                                                      补码乘法

范围在 -2w-1 ≤x, y ≤2w-1-1 内的整数 x 和 y 可以表示为 w 位的补码数字，但是它们的乘积 x · y 的取值范围在 -2w-1 · (2w-1-1) = -22w-2+2w-1 和 -2w-1 · -2w-1 = -22w-2 之间。要用补码来表示这
正文.indd   60 2010-10-19   14:18:38
第 2 章 　 信 息 的 表 示 和 处 理 　 　 6 1 　
个乘积，可能需要 2w 位—大多数情况下只需要 2w-1 位，但是特殊情况 22w-2 需要 2w 位（包 括一个符号位 0）。然而， C 语言中的有符号乘法是通过将 2w 位的乘积截断为 w 位的方式实现的。 根据等式（2-10），w 位的补码乘法运算 *  w t 的结果为 ： x *  w t y = U2Tw((x · y) mod 2w)                                                (2-17) 我们认为对于无符号和补码乘法来说，乘法运算的位级表示都是一样的。也就是，给定长度 为 w 的位向量 x → 和 y →，无符号乘积 B2Uw( x →)*  w u B2Uw( y →) 的位级表示与补码乘积 B2Tw( x →)*  w t B2Tw( y →) 的位级表示是相同的。这表明机器可以用一种乘法指令来进行有符号和无符号整数的乘法。 举例说明，图 2-26 给出了不同 3 位数字的乘法结果。对于每一对位级运算数，我们执行无 符号和补码乘法，得到 6 位的乘积，然后再把这些乘积截断到 3 位。无符号的截断后的乘积总是 等于 x · y mod 8。虽然无符号和补码两种乘法乘积的 6 位表示不同，但是截断后的乘积的位级表 示都相同。

XDR 库中的安全漏洞

2002 年，人们发现 Sun Microsystems 公司提供的实现 XDR 库的代码有安全漏洞，XDR 库 是一个广泛使用的程序间共享数据结构的工具，造成这个安全漏洞的原因是程序会在毫无察觉的 情况下产生乘法溢出。

乘以常数

在大多数机器上，整数乘法指令相当慢，需要 10 个或者更多的时钟周期，然而其他整数运 算（例如加法、减法、位级运算和移位）只需要 1 个时钟周期。因此，编译器使用了一项重要的 优化，试着用移位和加法运算的组合来代替乘以常数因子的乘法。首先，我们会考虑乘以 2 的幂 的情况，然后再概括成乘以任意常数。 设 x 为位模式 [xw-1, xw-2,…, x0] 表示的无符号整数。那么，对于任何 k ≥ 0，我们都认为 [xw-1, xw-2,…, x0, 0,…, 0] 给出了 x2k 的位级表示，这里右边增加了 k 个 0。这个属性可以通过等式 （2-1）推导出来 ：
B2Uw+k([xw−1,xw−2,...,x 0, 0,...,0])=
w−1 � i=0
xi2i+k =�w−1 � i=0 xi2i�. 2k =x2k 对于 k<w，我们可以将移位后的位向量截断到长度 w，得到 [xw-k-1, xw-k-2,…, x0, 0,…, 0]。根 据等式（2-9），这个位向量的数值为 x2kmod2w ＝ x*w t2k。因此，对于无符号变量 x，C 表达 式 x<<k等价于x*pwr2k，这里pwr2k等于2k。特别地，我们可以用1U<<k来计算pwr2k。 通过类似的推理，我们可以得出，对于一个位模式为 [xw-1, xw-2,…, x0] 的补码数 x，以及范围 在 0≤k < w 内任意的 k，位模式 [xw-k-1, xw-k-2,…, x0, 0,…, 0] 就是 x*w t2k 的补码表示。因此，对于 有符号变量x，C 表达式x<<k等价于x * pwr2k，这里pwr2k等于2k。 注意，无论是无符号运算还是补码运算，乘以 2 的幂都可能会导致溢出。结果表明，即使溢 出的时候，我们通过移位得到的结果也是一样的。 由于整数乘法比移位和加法的代价要大得多，许多 C 语言编译器试图以移位、加法和减法 的组合来消除很多整数乘以常数的情况。例如，假设一个程序包含表达式x*14。利用等式 14 = 23 + 22 + 21，编译器会将乘法重写为(x<<3)+(x<<2)+(x<<1)，实现了将一个乘法替换为三个 移位和两个加法。无论x是无符号的还是补码，甚至当乘法会导致溢出时，两个计算都会得到 ……
正文.indd   63 2010-10-19   14:18:40
　 6 4 　　 第 一 部 分 　 程 序 结 构 和 执 行 　
一样的结果。（根据整数运算的属性可以证明这一点。）更好的方法是，编译器还可以利用属性 14 = 24 - 21，将乘法重写为(x<<4)-(x<<1)，这时只需要两个移位和一个减法。

除以 2 的幂

在大多数机器上，整数除法要比整数乘法更慢—需要 30 个或者更多的时钟周期。除以 2 的幂也可以用移位运算来实现，只不过我们用的是右移，而不是左移。无符号和补码数分别使用 逻辑移位和算术移位来达到目的。 整数除法总是舍入到零。对于 x≥0 和 y > 0，结果是ԏx/y」，这里对于任何实数 a，ԏa」 定 义为唯一的整数 a'，使得 a'≤ a < a'+ 1。例如，ԏ3.14」 =3，ԏ
3.14」 = -4，而ԏ3」 = 3。 考虑对一个无符号数执行逻辑右移 k 位的效果。我们认为这和除以 2k 有一样的效果。例如， 图 2-27 给出了在 12 340 的 16 位表示上执行逻辑右移的结果，以及对它执行除以 1、2、16 和 256 的结果。从左端移入的 0 以斜体表示。我们还给出了如果用真正的运算去做除法得到的结 果。这些示例说明，移位总是舍入到零，这一结果与整数除法的规则一样。

关于整数运算的最后思考

正如我们看到的，计算机执行的“整数”运算实际上是一种模运算形式。表示数字的有限字 长限制了可能的值的取值范围，结果运算可能溢出。我们还看到，补码表示提供了一种既能表示 负数也能表示正数的灵活方法，同时使用了与执行无符号算术相同的位级实现，这些运算包括加 法、减法、乘法，甚至除法，无论运算数是以无符号形式还是以补码形式表示的，都有完全一样 或者非常类似的位级行为。 我们看到了 C 语言中的某些规定可能会产生令人意想不到的结果，而这些可能是难以察觉 和理解的缺陷的源头。我们特别看到了unsigned数据类型，虽然它概念上很简单，但可能导 致即使是资深程序员都意想不到的行为。我们还看到这种数据类型会以出乎意料的方式出现，比 如，当书写整数常数和当调用库函数时。

二进制小数

理解浮点数的第一步是考虑含有小数值的二进制数字。首先，让我们来看看更熟悉的十进制 表示法。十进制表示法使用的表示形式为 ：dmdm-1…d1d0.d-1d-2…d-n，其中每个十进制数 di 的取 值范围是 0 ～ 9。这个表示方法描述的数值 d 定义如下 ： d = m �i =−n 10i ×di 数字权的定义与十进制小数点符号（‘.’）相关，这意味着小数点左边的数字的权是 10 的正 幂，得到整数值，而小数点右边的数字的权是 10 的负幂，得到小数值。例如，12.3410 表示数字 3×10−1+4×10−2=12 34 100. By analogy, consider a notation of the form representsthenumber1×101+2×100+ 。 类似地，考虑一个形如 bmbm-1…b1b0.b-1b-2…b-n-1b-n 的表示法，其中每个二进制数字，或者 称为位，bi 的取值范围是 0 和 1，如图 2-30 所示。这种表示方法表示的数 b 定义如下 ： b= m �i =−n 2i ×bi                  　　　　　　　　　　　　（2-19） 符号‘.’现在变为了二进制的点，点左边的位的权是 2 的正幂，点右边的位的权是 2 的负幂。 例如，101.112 表示数字 represents the number 1×22+0×21+1×20+1× 2 2−1+1×2−2=4+0+1+ 1 2 + 1 4 =53 4.。

IEEE 浮点表示

前一节中谈到的定点表示法不能很有效地表示非常大的数字。例如，表达式 5 × 2100 是用 101 后面跟随 100 个零组成的位模式来表示。相反地，我们希望通过给定 x 和 y 的值，来表示形 如 x × 2y 的数。 IEEE 浮点标准用 V = (-1)s × M × 2E 的形式来表示一个数 ： •  符号（sign）　s 决定这个数是负数（s=1）还是正数（s=0），而对于数值 0 的符号位解释作 为特殊情况处理。 •  尾数（significand）　M 是一个二进制小数，它的范围是 1 ～ 2-ε，或者是 0 ～ 1-ε。 •  阶码（exponent）　E 的作用是对浮点数加权，这个权重是 2 的 E 次幂（可能是负数）。 将浮点数的位表示划分为三个字段，分别对这些值进行编码 ： •  一个单独的符号位 s 直接编码符号 s。 •  k 位的阶码字段exp = ek-1…e1e0 编码阶码 E。 •  n 位小数字段frac = fn-1…f1 f0 编码尾数 M，但是编码出来的值也依赖于阶码字段的值是否 等于 0。 图 2-31 给出了将这三个字段装进字中两种最常见的格式。在单精度浮点格式（C 语言中的 float）中，s、exp和frac字段分别为 1 位、k = 8 位和 n = 23 位，得到一个 32 位的表示。 在双精度浮点格式（C 语言中的double）中，s、exp和frac字段分别为 1 位、k = 11 位和 n = 52 位，得到一个 64 位的表示。

例题：A.  对于一种具有 n 位小数的浮点格式，给出不能准确描述的最小正整数的公式（因为要想准确表示它 需要 n+1 位小数）。假设阶码字段长度 k 足够大，可以表示的阶码范围不会限制这个问题。 B. 对于单精度格式（n = 23），这个整数的数字值是多少？

例题：

在练习题2.46中我们看到，爱国者导弹软件将0.1近似表示为x = 0.000110011001100110011002。 假设使用IEEE舍入到偶数方式确定0.1的二进制小数点右边23位的近似表示x'。 A. x' 的二进制表示是什么？ B. x' - 0.1 的十进制表示的近似值是什么？ C. 运行 100 小时后，计算时钟值会有多少偏差？ D. 该程序对飞毛腿导弹位置的预测会有多少偏差？

浮点运算

IEEE 标准指定了一个简单的规则，用来确定诸如加法和乘法这样的算术运算的结果。把浮 点值 x 和 y 看成实数，而某个运算⊙定义在实数上，计算将产生 Round (x ⊙ y)，这是对实际运算 的精确结果进行舍入后的结果。在实际中，浮点单元的设计者使用一些聪明的小技巧来避免执行 这种精确的计算，因为计算只要精确到能够保证得到一个正确的舍入结果就可以了。当参数中有 一个是特殊值（如 -0、- ∞或 NaN）时，IEEE 标准定义了一些使之更合理的规则。例如，定义 1/-0 将产生 - ∞，而定义 1/+0 会产生 + ∞。

网络旁注 DATA ：IA32-FP ：Intel IA32 的浮点运算 在下一章，我们将深入研究 Intel IA32 处理器，这种处理器大量地应用于今天的个人计算机 中。这里，我们重点突出这种机器的一个特性，即用 GCC 编译的时候，它能够严重影响程序对 浮点数运算的行为。

Ariane 5—浮点溢出的高昂代价 将大的浮点数转换成整数是一种常见的程序错误来源。1996 年 6 月 4 日，Ariane 5 火箭初次 航行，一个错误便产生了灾难性的后果。发射后仅仅 37 秒，火箭偏离了它的飞行路径，解体并 且爆炸。火箭上载有价值 5 亿美元的通信卫星。

 

 

小结
计算机将信息按位编码，通常组织成字节序列。用不同的编码方式表示整数、实数和字符 串。不同的计算机模型在编码数字和多字节数据中的字节排序时使用不同的约定。 C 语言的设计可以包容多种不同字长和数字编码的实现。虽然高端机器逐渐开始使用 64 位 字长，但是目前大多数机器仍使用 32 位字长。大多数机器对整数使用补码编码，而对浮点数使 用 IEEE 浮点编码。在位级上理解这些编码，并且理解算术运算的数学特性，对于想使编写的程 序能在全部数值范围上正确运算的程序员来说，是很重要的。

精选例题解析：

1.只使用位级和逻辑运算，编写一个 C 表达式，它等价于x==y。换句话说，当x和y相 等时它将返回 1，否则就返回 0。

这个表达式是 !（x^y）。 也就是，当且仅当x的每一位和y相应的每一位匹配时，x^y等于零。然后，我们利用!来判定一个 字是否包含任何非零位。 没有任何实际的理由要去使用这个表达式，因为可以简单地写成 x==y，但是它说明了位级运算和逻 辑运算之间的一些细微差别。

2.在第 3 章，我们将看到由反汇编器生成的列表，反汇编器是一种将可执行程序文件转换 回可读性更好的 ASCII 码形式的程序。这些文件包含许多十六进制数字，都是用典型的补码形式来表示 这些值。能够认识这些数字并理解它们的意义（例如，它们是正数还是负数），是一项重要的技巧。 　　在下面的列表中，对于标号为 A ～ J（标记在右边）的那些行，将指令名（sub、mov和add） 右边显示的（用 32 位补码形式表示的）十六进制值转换为等价的十进制值。
8048337: 81 ec b8 01 00 00 sub $0x1b8,%esp A. 804833d: 8b 55 08 mov 0x8(%ebp),%edx 8048340: 83 c2 14 add $0x14,%edx B. 8048343: 8b 85 58 fe ff ff mov 0xfffffe58(%ebp),%eax C. 8048349: 03 02 add (%edx),%eax 804834b: 89 85 74 fe ff ff mov %eax,0xfffffe74(%ebp) D. 8048351: 8b 55 08 mov 0x8(%ebp),%edx 8048354: 83 c2 44 add $0x44,%edx E. 8048357: 8b 85 c8 fe ff ff mov 0xfffffec8(%ebp),%eax F. 804835d: 89 02 mov %eax,(%edx) 804835f: 8b 45 10 mov 0x10(%ebp),%eax G. 8048362: 03 45 0c add 0xc(%ebp),%eax H. 8048365: 89 85 ec fe ff ff mov %eax,0xfffffeec(%ebp) I. 804836b: 8b 45 08 mov 0x8(%ebp),%eax 804836e: 83 c0 20 add $0x20,%eax J. 8048371: 8b 00 mov (%eax),%eax

对于 32 位的机器，由 8 个十六进制数字组成，而且开始的那个数字在 8 ～ f 之间的任何值， 都是一个负数。数字以 f 串开头是很普遍的事情，因为负数的起始位全为 1。不过，你必须看仔细了。例 如，数0x8048337仅仅有 7 个数字。把起始位填入 0，从而得到0x08048337，这是一个正数。

3.你的同事对你补码加法溢出条件的分析有些不耐烦了，他给出了一个函数tadd_ok的 实现，如下所示 ：
/* Determine whether arguments can be added without overflow */ /* WARNING: This code is buggy. */ int tadd_ok(int x, int y) { int sum = x+y; return (sum-x == y) && (sum-y == x); }
你看了代码以后笑了。解释一下为什么。

通过对 2.3.2 节的学习，你的同事可能已经学会补码加上形成一个阿贝尔群，以及表达式 (x+y)-x求值得到y，无论加法是否溢出，而(x+y)-y总是会求值得到x。

4，写一个函数div16，对于整数参数x返回x/16的值。你的函数不能使用除法、模运 算、乘法、任何条件语句（if或者?:）、任何比较运算符（例如<、>或==）或任何循环。你可以假 设数据类型int是 32 位长，使用补码表示，而右移是算术右移。 现在我们看到，除以 2 的幂可以通过逻辑或者算术右移来实现。这也正是为什么大多数机器 上提供这两种类型的右移。不幸的是，这种方法不能推广到除以任意常数。同乘法不同，我们不 能用除以 2 的幂的除法来表示除以任意常数 K 的除法。

这里唯一的挑战是不用任何测试或条件运算计算偏置量。我们利用了一个诀窍，表达式 x>>31产生一个字，如果x是负数，这个字为全 1，否则为全 0。通过掩码屏蔽适当的位，我们就得到期 望的偏置值。

int div16(int x) { /* Compute bias to be either 0 (x >= 0) or 15 (x < 0) */ int bias = (x >> 31) & 0xF; return (x + bias) >> 4; }