0.PTA得分截图
1.本周学习总结
1.1 总结树及串内容
1.1.1 串
1.串的定义
串(String):零个或多个字符组成的有限序列。
2.串的应用
(1).文本编辑器
(2).Word、PPT等
(3).QQ
(4).网页
(5).查重
3.串的存储结构
(1)定长顺序存储表示
用一组地址连续的存储单元存储串值的字符序列,称为顺序串。可用一个数组来表示。
#define MaxSize 100 //MaxSize常量表示字符串最大长度。
typedef struct
{ char data[MaxSize];//data域存储字符串,
int length;//length域存储字符串长度,
} SqString;
(2)堆分配存储表示
特点:仍以一组地址连续的存储单元存放串值字符序列,但它们的存储空间是在程序执行过程中动态分配而得的。
typedef struct {
char *ch; // 若是非空串,则按串长分配存储区,
// 否则ch为NULL
int length; // 串长度
} HString;
ch=new char[length];
(3) 串的链式存储及其基本操作实现
链串的组织形式与一般的链表类似。
链串中的一个结点可以存储多个字符。通常将链串中每个结点所存储的字符个数称为结点大小。

链串的节点类型定义如下:
typedef struct snode
{ char data;
struct snode *next;
} LiString;
结构体定义如下:
#define CHUNKSIZE 80 //可由用户定义的块大小
typedef struct Chunk{
char ch[CHUNKSIZE];
struct Chunk *next;
}Chunk;
typedef struct{
Chunk *head,*tail; //串的头指针和尾指针
int curlen; //串的当前长度
}LString;
4.串的模式匹配算法
算法目的:
确定主串中所含子串第一次出现的位置(定位)。
即如何实现Index(s,t)函数。
主串s称为目标串,把子串t称为模式串,因此定位也称作模式匹配。
Index(s,t)函数:匹配成功,返回位置;不成功,返回-1。
算法种类:
BF算法(又称古典的、经典的、朴素的、穷举的)。
KMP算法(特点:速度快)。
(1) BF(Brute-Force)算法
亦称简单匹配算法,其基本思路是:
(1)从目标串s=“s0s1…sn-1”的第一个字符开始和模式串t=“t0t1…tm-1”中的第一个字符比较
(2)若相等,则继续逐个比较后续字符;
(3)否则从目标串s的第二个字符开始重新与模式串t的第一个字符进行比较。
(4)依次类推,若从模式串s的第i个字符开始,每个字符依次和目标串t中的对应字符相等,则匹配成功,该算法返回i;否则,匹配失败,函数返回-1。
例如,设目标串s=“aaaaab”,模式串t=“aaab”。s的长度为n(n=6),t的长度为m(m=4)。
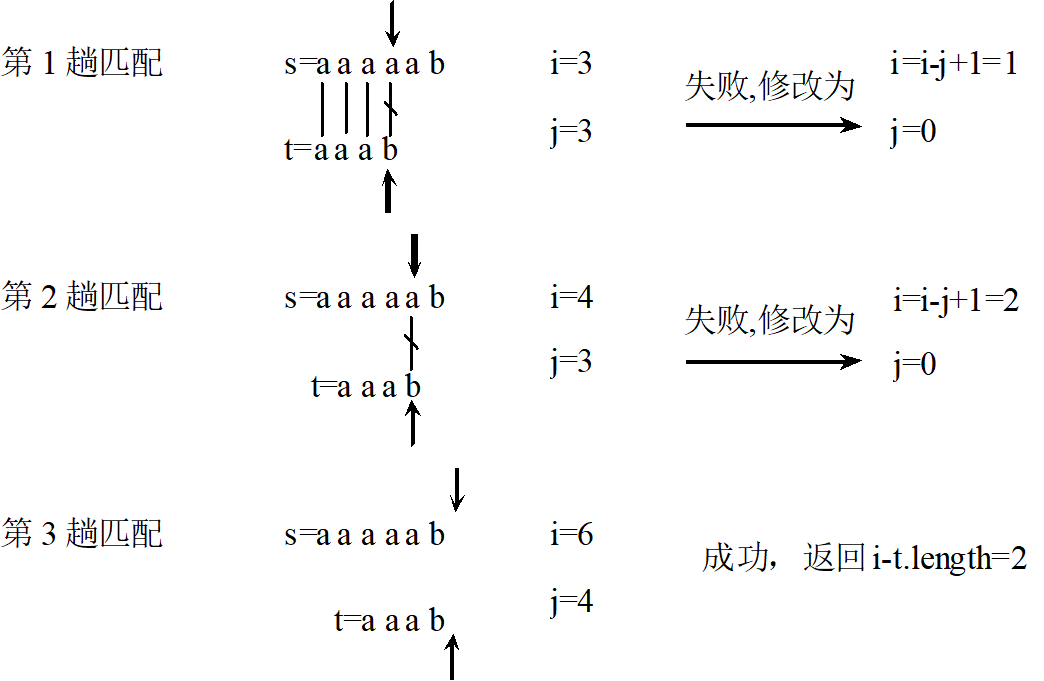
对应的BF算法如下:
int index(SqString s,SqString t)
{ int i=0, j=0;
while (i<s.length && j<t.length)
{ if (s.data[i]==t.data[j]) //继续匹配下一个字符
{ i++; //主串和子串依次匹配下一个字符
j++;
}
else //主串、子串指针回溯重新开始下一次匹配
{ i=i-j+1; //主串从下一个位置开始匹配
j=0; //子串从头开始匹配
}
}
if (j>=t.length)
return(i-t.length); //返回匹配的第一个字符的下标
else
return(-1); //模式匹配不成功
}
(2)KMP算法
KMP算法是D.E.Knuth、J.H.Morris和V.R.Pratt共同提出的,简称KMP算法。该算法较BF算法有较大改进。
改进之处:
1.主串不需回溯i指针
2.将模式串向右“滑动”尽可能远的一段距离
如何算next[j]?
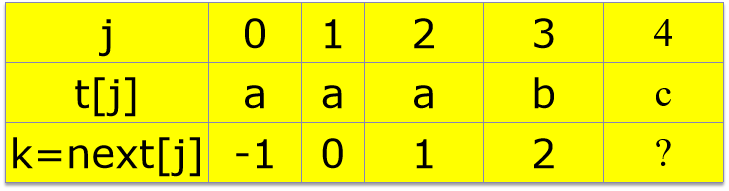
已知next[j]=k,tj=tk,
t0t1….......tk-1tk=tj-ktj-k+1…........tj-1tj
则next[j+1]=? k+1
已知next[j]=k,tj≠tk。
t0t1….......tk-1tk≠tj-ktj-k+1…........tj-1tj
则k=next[k]
由模式串t求出next值:
void GetNext(SqString t,int next[])
{ int j,k;
j=0;k=-1;next[0]=-1;
while (j<t.length-1)
{ if (k==-1 || t.data[j]==t.data[k])
{ j++;k++;
next[j]=k;
}
else k=next[k];
}
}
算法代码:
int KMPIndex(SqString s,SqString t)
{ int next[MaxSize],i=0,j=0;
GetNext(t,next);
while (i<s.length && j<t.length)
{ if (j==-1 || s.data[i]==t.data[j])
{ i++;
j++; //i,j各增1
}
else j=next[j]; //i不变,j后退
}
if (j>=t.length)
return(i-t.length); //匹配模式串首字符下标
else
return(-1); //返回不匹配标志
}
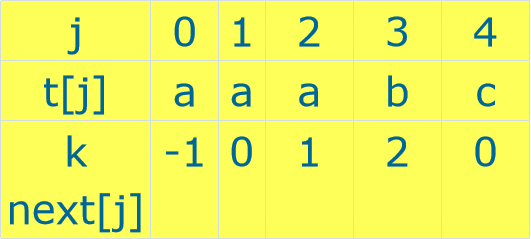
next数组改进:nextval数组

j=1
t[1]='a',k=next[j]=0; t[0]='a'
t[j]==t[k] nextval[j]=next[k]
修正为next[k]=-1
j=4
t[4]='b',k=next[j]=3; t[3]='a'
t[j]!=t[k] nextval[j]=next[j]
不修正,等于next[j]=3
将next[j]修正为nextval[j]。
t.data[j]?=t.data[next[j])
1.若不等,则 nextval[j]=next[j];
2.若相等nextval[j]=nextval[k]。
next数组缺陷

由模式串t求出nextval值:
void GetNextval(SqString t,int nextval[])
{ int j=0,k=-1;
nextval[0]=-1;
while (j<t.length)
{ if (k==-1 || t.data[j]==t.data[k])
{ j++;k++;
if (t.data[j]!=t.data[k])
nextval[j]=k;
else
nextval[j]=nextval[k];
}
else
k=nextval[k];
}
}
修改后的KMP算法:
int KMPIndex1(SqString s,SqString t)
{ int nextval[MaxSize],i=0,j=0;
GetNextval(t,nextval);
while (i<s.length && j<t.length)
{ if (j==-1 || s.data[i]==t.data[j])
{ i++;
j++;
}
else
j=nextval[j];
}
if (j>=t.length)
return(i-t.length);
else
return(-1);
}
1.1.2树和二叉树
1.树的概念
(1)树的定义
树型结构:
非线性结构
现实世界中描述层次结构的关系:
操作系统的文件系统、Internet中的DNS(域名系统)、人类的族谱等
计算机领域中:编译器语法结构、数据库系统、分析算法:人工智能、数据挖掘算法。
(2)基本术语
根:即根结点(没有前驱)
叶子: 即终端结点(没有后继)
森林:指m棵不相交的树的集合(例如删除A后的子树个数)
有序树:结点各子树从左至右有序,不能互换(左为第一)
无序树:结点各子树可互换位置。
双亲:即上层的那个结点(直接前驱)
孩子:即下层结点的子树的根(直接后继)
兄弟:同一双亲下的同层结点(孩子之间互称兄弟)
祖先:即从根到该结点所经分支的所有结点
子孙:即该结点下层子树中的任一结点
结点:即树的数据元素
结点的度:结点挂接的子树数,分支数目
结点的层次:从根到该结点的层数(根结点算第一层)
终端结点:即度为0的结点,即叶子
分支结点:即度不为0的结点(也称为内部结点)
树的深度(或高度):指所有结点中最大的层数
2.二叉树
(1)定义
定义:是n(n>=0)个结点的有限集合,它或为空树(n=0),或由一个根结点和至多两棵称为根的左子树和右子树的互不相交的二叉树组成。
注:二叉树中不存在度大于2的结点,并且二叉树的子树有左子树和右子树之分。
(2)二叉树的五种基本形态:
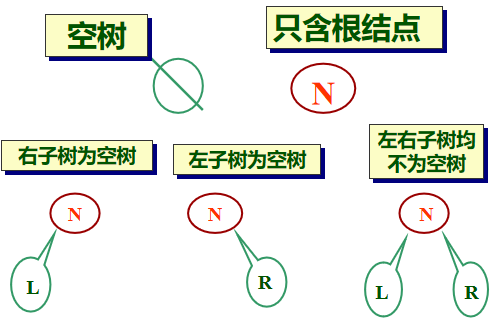
满二叉树:
在一棵二叉树中:
如果所有分支结点都有双分结点;
并且叶结点都集中在二叉树的最下一层。
二叉树结点:
高度为h的二叉树恰好有2h-1 个结点。
完全二叉树:
定义:深度为k 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k 的满二叉树中编号从1至n的结点一一对应
没有单独右分支结点
完全二叉树实际上是对应的满二叉树删除叶结点层最右边若干个结点得到的。
性质: n1=0或者n1=1。n1可由n的奇偶性确定:n为奇数,n1=0;n为偶数,n1=1。
如果有度为1节点,只可能有一个,且该结点只有左孩子无右孩子。
除树根结点外,若一个结点的编号为i,则它的双亲结点的编号为i/2。
若编号为i的结点有左孩子结点,则左孩子结点的编号为2i;若编号为i的结点有右孩子结点,则右孩子结点的编号为2i+1。
若i≤n/2,则编号为i的结点为分支结点,否则为叶结点。
满二叉树和完全二叉树的区别:
满二叉树是叶子一个也不少的树,而完全二叉树虽然前n-1层是满的,但最底层却允许在右边缺少连续若干个结点。满二叉树是完全二叉树的一个特例。
(3) 二叉树性质
性质1 非空二叉树上叶节点数等于双分支节点数加1。
性质2:在二叉树的第 i 层上至多有 2^i-1 个结点(i≥1)。
性质3 高度为h的二叉树至多有2^h-1个节点(h≥1)。
性质4: 具有n个结点的完全二叉树的深度必为log2n+1
3.二叉树存储结构
(1)二叉树的顺序存储结构
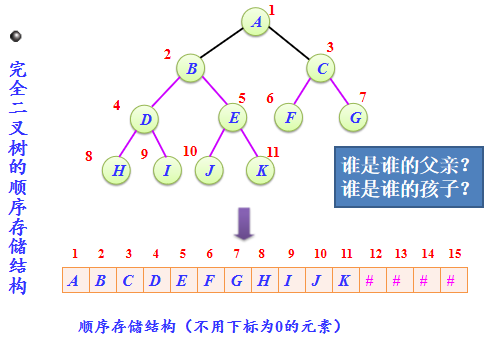
第i个结点:
父亲:i/2
左孩子:2i 右孩子:2i+1
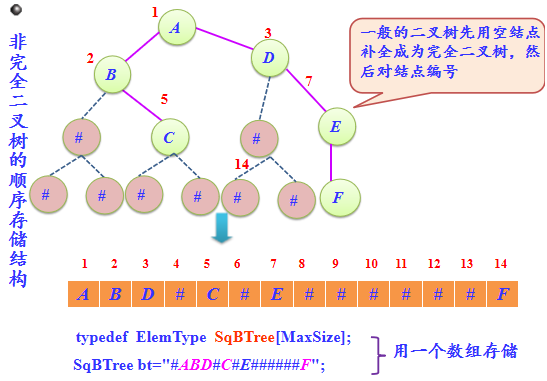
二叉树顺序存储结构缺点
对于完全二叉树来说,其顺序存储是十分合适
在最坏的情况下,一个深度为k且只有k个结点的单支树(树中不存在度为2的结点)却需要2k-1的一维数组。空间利用率太低!
数组,查找、插入删除不方便。
(2)二叉树的链式存储结构
在二叉树的链式存储中,结点的类型定义如下:
typedef struct node
{ ElemType data;
struct node *lchild, *rchild;
} BTNode;
typedef BTNode *BTree;
在二叉链中,n个结点,指针域个数:2n
分支数:n-1
空指针域个数 n+1
(3)二叉树创建方法:二叉树的顺序存储结构转成二叉链
创建编号i为根结点BT
创建左子树BT->lchild?
BT->lchild->data=Tree[2*i]
创建右子树BT->rchild?
BT->rchild->data=Tree[2*i+1]



