Codeforces Round #282 (Div. 1) B. Obsessive String

B. Obsessive String

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Hamed has recently found a string t and suddenly became quite fond of it. He spent several days trying to find all occurrences of t in other strings he had. Finally he became tired and started thinking about the following problem. Given a string s how many ways are there to extract k ≥ 1 non-overlapping substrings from it such that each of them contains string t as a substring? More formally, you need to calculate the number of ways to choose two sequences a1, a2, ..., ak and b1, b2, ..., bk satisfying the following requirements:

• k ≥ 1
• 
• 
• 
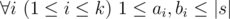
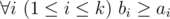
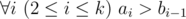
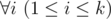•   t is a substring of string saisai + 1... sbi (string s is considered as 1-indexed).

As the number of ways can be rather large print it modulo 109 + 7.

Input

Input consists of two lines containing strings s and t (1 ≤ |s|, |t| ≤ 105). Each string consists of lowercase Latin letters.

Output

Print the answer in a single line.

Sample test(s)

input

ababa
aba

output

5

input

welcometoroundtwohundredandeightytwo
d

output

274201

input

ddd
d

output

12

思路： 首先用KMP求出匹配的位置；
      dp[i][j] 变示包含a[i]的匹配分成 j 段的方案，
      sum[i][j]是前 i 个字母，分成 j 段的方案(也就是不一定包含a[i])
      即 sum[i][j]=sum(dp[k][j]) ; k <= i ;
      定义 e[i][j] = sum(sum[k][j]) k <= i ;
      如果i不是匹配的节点
      dp[i][j]=dp[i-1][j];
      如果 i 是匹配的节点；
      那么 dp[i][j] = e[i-m][j-1];（j>=2）
      dp[i][1]=i-m+2; 
      即枚举a[i]和谁在一起
      先得到下面的转移（假设|a|/|b| < 10）

         int ans=0;
         if(m==1&&a[0]==b[0])
         {
             dp[0][1]=1;
             sum[0][1]=1;
             e[0][1]=1;
             ans++;
         }
         for( i = 1 ; i < n ;i++)
         {
             for(j = 1 ; j < 10 ;j++)
                dp[i][j]=dp[i-1][j] ;
             if(vi[i])
             {
                 dp[i][1]=i-m+2;
                 if(i==m-1);
                 else
                 for( j = 2; j < 10 ;j++){
                    dp[i][j]=(e[i-m][j-1]);
                 }
             }
             for(j = 1 ; j < 10 ;j++){
                ans+=dp[i][j];
                sum[i][j]=sum[i-1][j]+dp[i][j];
                e[i][j]=e[i-1][j]+sum[i][j];
             }
         }
         cout << ans << endl;

　　不过我们发现这样内存和时间都不能承受‘；

     观察发现，第二维可以不要；

     后面得到的代码是：

    

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<cmath>
#define LL long long
#define maxn 100010
#define eps 1e-9
#define mod 1000000007
using namespace std;

LL dp[maxn] ,f[maxn];
LL sum[maxn],e[maxn];
char a[maxn],b[maxn] ;
bool vi[maxn] ;
void getNext()
{
    int n,j,i;
    j=-1;
    f[0]=-1;
    n=strlen(b) ;
    for( i = 1 ; i < n ;i++)
    {
        while(j>=0&&b[j+1] != b[i])j=f[j] ;
        if(b[j+1]==b[i])j++ ;
        f[i]=j;
    }
}
void KMP()
{
    int n,m,i,j;
    j=-1;
    getNext();
    n=strlen(a) ;
    m=strlen(b) ;
    memset(vi,0,sizeof(vi));
    for( i = 0 ; i < n ;i++)
    {
        while( j >= 0 && b[j+1] != a[i])j=f[j] ;
        if(b[j+1]==a[i]) j++ ;
        if(j==m-1)
        {
            vi[i]=true;
        }
    }
}
int main()
{
    int i,n,m,j,k,id;
    int T,case1=0,len ;
    while(scanf("%s%s",a,b) != EOF)
    {
         KMP();
         n = strlen(a) ;
         m = strlen(b) ;
         memset(dp,0,sizeof(dp)) ;
         memset(sum,0,sizeof(sum)) ;
         memset(e,0,sizeof(e));
         int ans=0;
         if(m==1&&a[0]==b[0])
         {
             dp[0]=1;
             sum[0]=1;
             e[0]=1;
             ans++;
         }
         for( i = 1 ; i < n ;i++)
         {
             dp[i]=dp[i-1] ;
             if(vi[i])
             {
                 dp[i]=i-m+2;
                 if(i==m-1);
                 else{
                   dp[i] += e[i-m] ;
                   dp[i] %= mod;
                 }
             }
             ans+=dp[i];
             ans%= mod;
             sum[i]=sum[i-1]+dp[i];
             sum[i] %=mod;
             e[i]=e[i-1]+sum[i];
             e[i] %= mod;
        }
        cout << ans << endl;
    }
    return 0 ;
}