Codeforces Round #176 (Div. 1) B. Shifting
John Doe has found the beautiful permutation formula.
Let's take permutation p = p1, p2, ..., pn. Let's define transformation f of this permutation:
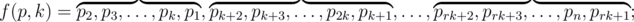
where k (k > 1) is an integer, the transformation parameter, r is such maximum integer that rk ≤ n. If rk = n, then elements prk + 1, prk + 2 and so on are omitted. In other words, the described transformation of permutation p cyclically shifts to the left each consecutive block of length k and the last block with the length equal to the remainder after dividing n by k.
John Doe thinks that permutation f(f( ... f(p = [1, 2, ..., n], 2) ... , n - 1), n) is beautiful. Unfortunately, he cannot quickly find the beautiful permutation he's interested in. That's why he asked you to help him.
Your task is to find a beautiful permutation for the given n. For clarifications, see the notes to the third sample.
A single line contains integer n (2 ≤ n ≤ 106).
Print n distinct space-separated integers from 1 to n — a beautiful permutation of size n.
2
2 1
3
1 3 2
4
4 2 3 1
A note to the third test sample:
- f([1, 2, 3, 4], 2) = [2, 1, 4, 3]
- f([2, 1, 4, 3], 3) = [1, 4, 2, 3]
- f([1, 4, 2, 3], 4) = [4, 2, 3, 1]
思路: 每次修改,相当于 把 1的位置放到 k+1 , k+1的放到 2*k+1 ,2*k+1放到3*k+1上面
每次这样模拟就可以了

#include <stdio.h> #include <math.h> #include <string.h> #include <iostream> #include <vector> #include <map> #include <queue> #include <algorithm> #define LL long long #define maxn 1000010 #define INF 0x3f3f3f3f #define mod 1000000007 using namespace std; int ans[maxn*3] ,L,R ; void change(int n,int k ) { int m = n/k ,s ,tmp =ans[L]; if(n%k==0)m--; for( int i = 1 ; i <= m ;i++) { s=i*k+L; swap(ans[s],tmp) ; } L++; R++; ans[R]=tmp; } void out(int n) { cout<<ans[L++]; for(int i = 2 ; i <= n ;i++) printf(" %d",ans[L++]) ; puts("") ; } int main() { int i ,x,y; int j,n,m,pre,sz; while(scanf("%d",&n) != EOF) { for( i =1 ; i <= n ;i++) ans[i]=i; L=1;R=n; for( i = 2 ; i <= n ;i++){ change(n,i) ; } out(n); } return 0 ; }




