数据结构：数组，堆栈，队列，链表，树

所谓的数据结构就是表示数据之间的关系。这些数据结构中的每一个元素都是紧密相连的，不能有空隙。

数据结构是抽象的概念，没有语言之别，就像是设计模式一样，是一种抽象的思想，用任何语言的代码都能构建出来。而我们的python中的字符串，列表，字典，元祖，集合都是基本数据类型，他们是依附于语言存在的，不同的语言有不同的基本数据类型。

 

在二进制下的数据类型所占的位数：

int8位

longint16位

shortint4位

char---assic8位；gbk16位；utf-8，24位；unicode32位；

float--占4个字节，即32位，具体分布如下：1bit（符号位，即正负号），8bit（指数位），23bit（尾数位）。

数组

数组是一维图形。

数组是定长，所谓的定长就是在创建之初就需要告诉解释器它的长度，而我们的列表是不定长的，所谓的不定长就是我们创建了一个列表，我们肉眼看到的可能这个列表只有3个元素或者我们就干脆创建一个空列表，但是在内部实现的时候解释器给这个列表一个初始长度，假设这个长度是20，然后我们对这个我们所创建了列表进行增删改查的时候，这个列表的长度就会发生变化，然后发生变化的过程中，系统内部就把这个列表一开始的所有数据给拷贝下来，然后根据你增删改查的结果对列表进行扩大或者缩小。

数组中的数据类型必须要保持一致，一个数组中只能存一种数据类型，所谓的数据类型就是：整数int，小数float，字符串char这些类型。列表里面存的数据类型是不一样的，但是在解释器内部，这些个不同的数据类型都是被python实例化出来的一个个对象，然后在列表中存的都是这些对象的一个个的地址指针。

数组可以通过索引取值，时间复杂度是O1.（O1这个时间复杂度跟数组的规模是没有差别的，不论是多长的数组，它的时间复杂度都是O1.而On的话，这个n可以是任何常数，比如可以是20、300、5000等等，都远远没有O1快）它的取值原理是因为数组存的是同一种数据类型，而数据类型都是固定长度的，所以可以通过长度取值。比如这里有一个数组A，它存的都是整数类型，第一个元素的地址假设是0110，那么我们要获取这个A数组中的第4个元素，只需要通过第一个元素的地址加上（4-1）*8=24，即0110+24=0134，就是第4个元素的地址，然后就能直接很快地拿到这个元素，内存地址都是连续的。这就是它取值快的地方。但是它有弊端，我们的数组中每一个元素都是紧挨着的，打一个比方，算盘，它的每一根柱子上都是一串算珠，我们把这个算盘立起来的时候，算珠都会垂直落到底部，我们假设拆掉一个柱子上的一个算珠，那么这个算珠上面的算珠会依次降落到下一个算珠的位置上，然后这个柱子的算珠整体高度就会下降一个算珠的高度，或者我们增加一个算珠，我们所增加的这个算珠上面的所有算珠都会上升到上一个算珠的位置上，因为算珠之间不能有空隙，要一个个紧紧挨着。我们的数组就类似这样的情况，当我们要在数组中插入一个值的时候，我们所插入的这个位置，后面的所有元素都要依次往后挪一个元素的位置，就像我们给算盘增加算珠一样，在增加的位置上的每一上面的算珠都要往上挪一个算珠的位置；同理，如果要删除一个数组中的元素的话，那么这个被删除的元素的位置就空出来了，然后因为我们的数组里面的元素都是紧挨着的，所以这个被删除的元素后面的元素都会依次往前挪一个元素的位置，就像我们的算盘上取掉一个算珠，这个算珠的上面每一个算珠都要往下降一个算珠的位置，就是这个道理。所以如果删除或者是插入一个数组中的中间元素的话，它后面的所有元素都需要挪动位置，这里就没有取值那么便捷了，时间复杂度就会增加，但是，如果是增加或者是删除最后一个元素就不会涉及到其他元素的操作，这里就不存在时间复杂度的增加问题了。

 

堆栈

堆栈也是一维图形。

我们想象一下一个装羽毛球的球桶，它的直径就是羽毛球的羽毛那一端所围成的圆形的直径，这样一个个羽毛球放进去刚好卡在桶壁内，没有多余空隙，以免晃动中产生摩擦带来不必要的损耗。假设这个球桶只有一个口，另一段是封死的，这个时候假设这个球桶是空的，我们把羽毛球一个个依次放进去的时候，只能从这个口放进去，然后也只能从这个口拿出来，也就是先进后出，后进先出。

在这个堆栈中我们只研究栈顶，这个栈顶的位置就是我们的堆栈整体高度。也就是说在这个羽毛球桶中，最上面的这个羽毛球在刻度4处，这个球桶中就有4个球，此时我们拿出去一个球，这个球桶中最上面的这个球就在3这个刻度上了，此时球桶中就有3个球，这个球桶中最上面的球就被我们标记为栈顶。实现一个堆栈的方式就是一个变量+一个数组。这个变量指向这个数组中的最后一个元素，比如这个数组中有8个元素，这个变量指向8，这个堆栈就有8个元素，栈顶就是8。

堆栈组成可以用列表实现，也可以用数组实现，如果用列表的话就可以存放不同的数据类型。

需要附上堆栈的代码实现，以上仅仅是概念性的原理。代码需要有一个类，类里面有两个方法，入栈和出栈，入栈时需要考虑到栈的大小，栈满时不可入，同时，出栈也要考虑到栈空时不能出。

# 自己实现一个堆栈，根据堆栈的特性，把类写出来，然后把里面的方法写出来
# 骚操作

class Stack(object):
    def __init__(self, arg):
        """
        初始化一个栈
        :param arg:栈的大小
        """
        self.arg = arg
        self.vessel = [0 for i in range(arg)]  # 栈所用的容器,返回值是0，
        # 才表明是一个空容器，否则如果返回i则是一个填满的容器
        self.top_heap = 0  # 栈顶标示

    def is_empty(self):
        """
        判断栈是否为空
        :return: 返回bool值
        """
        return False if self.arg > 0 else True

    def pop_stack(self):
        """
        如果栈有值，则出栈
        :return: 出栈
        """
        if self.top_heap <= 0:
            return "there is empty"
        else:
            # 这里要让栈顶移动位置，而不是直接用列表的pop方法，那样会改变容器的大小，
            self.top_heap -= 1 
            return self.vessel, self.vessel[self.top_heap]

    def push_stack(self, item):
        """
        :param item:
        :return:入栈
        """
        if self.top_heap + 1 > self.arg:
            raise Exception("栈溢出")
        else:
            # 同样这里是用赋值的方式，也是为了不改变容器的大小
            self.vessel[self.top_heap] = item
            self.top_heap += 1
            return self.vessel


obj = Stack(5)  

# obj.push_stack(50)
obj.pop_stack()
# obj.pop_stack()
# obj.pop_stack()
# obj.pop_stack()
# obj.pop_stack()
obj.push_stack(10)
obj.push_stack(13)
obj.push_stack(12)
obj.push_stack(12)
obj.push_stack(12)
# obj.push_stack(12)
print(obj.vessel,obj.top_heap)

 

 简单版，更好理解。

# 简单逻辑


class Stack(object):
    def __init__(self, arg):
        """
        初始化一个栈
        :param arg:栈的大小
        """
        self.arg = arg
        self.vessel = []

    def pop_stack(self):
        """
        如果栈有值，则出栈
        :return: 出栈
        """
        if self.is_empty() is True:
            raise Exception("there is already empty")
        else:
            self.vessel.pop()
            return self.vessel

    def push_stack(self, item):
        """
        :param item:
        :return:入栈
        """
        if self.is_full() is True:
            raise Exception("栈溢出")
        else:
            self.vessel.append(item)
            return self.vessel

    def is_empty(self):
        """
        判断栈是否为空
        :return: 返回bool值
        """
        return True if len(self.vessel) == 0 else False

    def is_full(self):
        """
        检查是否为满
        :return: 返回bool值
        """
        return True if len(self.vessel) == self.arg else False


obj = Stack(5)

# obj.push_stack(50)
# print(obj.pop_stack())
# obj.pop_stack()
obj.push_stack(10)
# obj.pop_stack()
obj.push_stack(15)

# obj.push_stack(22)
print(obj.vessel, obj.is_empty())

 

 

队列

队列也是一维图形。

队列不同于堆栈有一个口，进出都是它（我们叫做出入耦合），队列不一样，它有2个口，一个单独的出口，一个单独的入口（我们叫做出入分离）。同向时如果出入口重合，则队列为空，反向时如果出入口重合，则队列为满。我们在队列问题中，仅仅考虑两个点，入口和出口，而且这两个要分开考虑，不能想得过于复杂。所以按照堆栈的实现方式，队列的实现就是两个变量+数组。

队列同上，用数组和列表都能实现。

需要附上代码实现。

# 根据队列的特性，实现一个队列。单向队列
# 这里是有bug的，不过这个是骚操作，按照上面的栈的骚操作实现的


class Queue_piple():
    def __init__(self, size):
        self.size = size
        self.conduit = [0 for i in range(self.size)]
        self._inside = 0
        self._outside = 0

    def push(self, item):
        if self._inside + 1 >= self.size and self.conduit[0] is None:
            self._inside = 0

        elif self._inside + 1 > self.size:
            raise Exception("sorry, there is already full")
        self.conduit[self._inside] = item
        self._inside += 1
        print(self.conduit)
        return self.conduit

    def pop(self):
        if self._outside + 1 > self.size:
            raise Exception("sorry, there is already empty")
        else:
            self.conduit[self._outside] = None
            self._outside += 1
       
            return self.conduit


q_obj = Queue_piple(3)
q_obj.push(2)
q_obj.push(20)
q_obj.push(209)
q_obj.pop()
q_obj.pop()
# q_obj.pop()
q_obj.push(270)
q_obj.push(277)

print("hole thing", q_obj.conduit, q_obj._inside)

 

 这里是已经实现的简单逻辑的队列

# 简单逻辑，已经测过没有bug的队列。单向队列


class QueuePiple():

    def __init__(self, size):
        self.size = size
        self.conduit = []

    def push(self, item):
        if self.is_full() is True:
            raise Exception("there is already full")
        else:
            self.conduit.append(item)
            return self.conduit

    def pop(self):
        if self.is_empty() is True:
            raise Exception("there is already empty")
        else:
            self.conduit.remove(self.conduit[0])  # del self.conduit[0]
            return self.conduit

    def is_empty(self):
        return True if len(self.conduit) == 0 else False

    def is_full(self):
        return True if len(self.conduit) == self.size else False

    def get_size(self):
        return len(self.conduit)


q_obj = QueuePiple(3)
q_obj.push(2)
q_obj.push(20)
q_obj.push(209)
q_obj.pop()
# q_obj.pop()
# q_obj.pop()
q_obj.push(270)
q_obj.pop()
# q_obj.pop()
q_obj.pop()
# q_obj.pop()
q_obj.push(277)
print("hole thing", q_obj.conduit, q_obj.get_size())

 

 

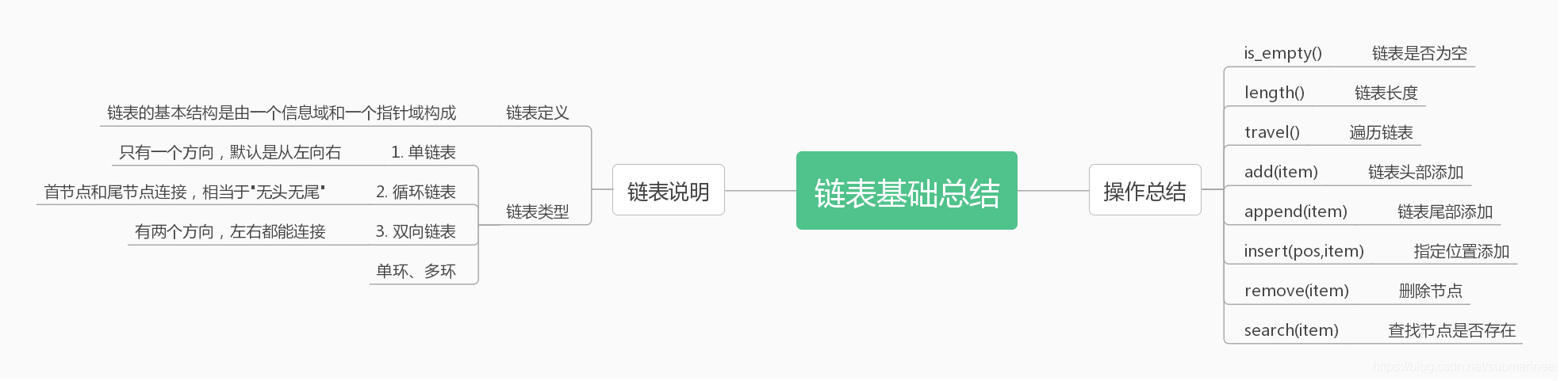
链表

链表也是一维图形。

链表中的每一个元素都会标记一个尾部指向，这个指向是指向下一个元素，然后每一个元素之间用尾部彼此相连，所谓链表就像铁链一样，彼此之间紧密相扣，形成一条链条。链表是没有大小的，不同于数组，堆栈和队列。

双向链表就是不仅会标记尾部指向，还会有头部指向，一条链表中的任意一个元素拿出来，它有头部指向，指向上一个元素，还有尾部指向，指向下一个元素，这就是双向链表。

链表分单向和双向，两种。彼此之间不能混合，单向和单向组合，双向和双向组合。循环链表，就是尾项指向头项，首位相连形成一个圆，就是循环链表，也就没有头尾之分。

链表的增删改查，跟数组比起来就要快很多了，比如我们要删除一个链表中的元素，就需要把这个元素的上一个元素的尾部指向指向到这个元素的下一个元素的尾部指向即可，就像是把这个链条上的一个链环拿掉就把这个链条分成了两截，然后把这个断开的部分重新链接上即可，比如是abcd的链条，把c拿掉，就让b和d链接上即可，不会涉及到更多元素的操作，比起数组就方便很多。但是有一点弊端，就是数组取值，是通过索引取值，会很快，而链表如果要取值，就需要从链头开始找依次去找到那个值然后返回，这样就会慢很多，如果刚好要找的那个值是链尾，那么就需要遍历整个链表。时间复杂度是O(n)。

 

需要附上代码实现，暂时还没有写出来，后续写出来，会附上。

书上粘下来的代码片段，链表构建的核心代码
q=Node（13）
q.next = head.next
head = q

下面附上完整版链表构建以及链表的增删改查 

# -*- encoding=utf8
"""
尝试构建链表数据结构。单向链表
"""


class ChainNode:
    """
    单向链表
    链表不同于队列和堆栈，他们有一个初始化的空容器（存储介质，比如list），
    链表是一个一个节点拼接而成，没有一个初始化的空容器，链表的初始化数据，需要单独创建。
    需要先有节点数据，节点中，有数据以及指针，再才能对这个初始化的只有一个节点的链表进行增删改查
    """
    def __init__(self, data):
        # 创建链表节点数据
        self.data = data
        # 创建链表指针
        self.next = None


class ChainList:
    """
    单向链表。对已经存在对链表进行增删改查等一系列操作
    """
    def __init__(self, node_=None):
        self.head = node_

    def is_empty(self):
        """
        链表是否为空
        :return:
        """
        return self.head is None

    def length(self):
        """
        链表长度
        :return:
        """
        length_count = 1
        current_node = self.head
        if not current_node:
            return 0
        while current_node.next is not None:
            # 拿到有效节点数据
            length_count += 1
            # 在循环体中，不断更新中间变量的值，让它依次向下移动，直至到最后一个节点
            current_node = current_node.next
        return length_count

    def travel(self):
        """
        遍历链表
        :return:
        """
        result_nodes = []
        current_node = self.head
        if self.length() <= 1:
            # 如果没有节点｜只有一个节点，current_node.next要么报错（没有节点的情况下），
            # 要么是None（只有一个节点的情况下），都不必走下面的循环，在这里直接拦截返回
            # print(current_node.data)
            result_nodes.append(current_node.data)
            return result_nodes
        while current_node is not None:
            # 这里是把每一个有效节点数据，都打印出来
            # print(current_node.data)
            result_nodes.append(current_node.data)
            current_node = current_node.next
        return result_nodes

    def add(self, item):
        """
        链表头部添加
        :param item:
        :return:
        """
        # 创建链表节点
        node_ = ChainNode(item)
        # 把现有链表挂载到新增的数据节点上
        node_.next = self.head
        # 挂载完成之后，替换链表的head，使head永远处于第一个节点位置
        self.head = node_

    def append(self, item):
        """
        链表尾部添加
        :param item:
        :return:
        """
        len_chain_ = self.length()
        last_node = self.head
        for i in range(len_chain_-1):
            # 这里不能遍历到最后一个，要遍历至倒数第二个，
            last_node = last_node.next
        # 这里走完所有循环，last_node就是最后一个节点对象，
        # 把新增的节点data挂载到它的next上，这样就追加完成
        append_item = ChainNode(item)
        last_node.next = append_item

    def insert(self, position, item):
        """
        在指定位置添加节点
        :param position:指定位置
        :param item:节点
        :return:
        """
        len_chain = self.length()
        if position <= 0:
            # 处理左边边界情况，如果插入的位置小于等于0，就直接调用add，放在第一个节点位置
            self.add(item)
            return
        if position > len_chain-1:
            # 处理右边边界情况，如果插入的位置大于链表长度，就直接调用append，放在最后一个节点位置
            self.append(item)
            return
        # 设置中间变量，next_node用来存储下一个节点
        next_node = self.head
        # temp_last_node用来存储上一个节点
        temp_last_node = None
        for i in range(len_chain):
            if i == position:
                # 如果找到需要插入的索引位置，就开始构建节点对象
                insert_node = ChainNode(item)
                # 把下一个节点数据挂载到插入的节点对象的next下面
                insert_node.next = next_node
                # 把插入的节点对象，挂载到上一个节点对象的next下面
                temp_last_node.next = insert_node
            # 存储上一个节点对象
            temp_last_node = next_node
            # 存储下一个节点对象
            next_node = next_node.next

    def remove(self, item):
        """
        删除节点
        找到所要删除的节点，把它的上下两个指针拼接上，该节点就自动被卸下，即删除
        :param item:
        :return:
        """
        next_node = self.head
        break_before_node = None
        if self.head.data == item:
            self.head = next_node.next
            return
        while next_node is not None:
            if next_node.data == item:
                break_before_node.next = next_node.next
                return
            break_before_node = next_node
            next_node = next_node.next

    def search(self, item):
        """
        查找节点是否存在
        比较类似于travel方法，就是在其中增加一层判断
        :param item:
        :return:
        """
        current_node = self.head
        length_chain = self.length()
        # 如果没有节点｜只有一个节点，current_node.next要么报错（没有节点的情况下），
        # 要么是None（只有一个节点的情况下），都不必走下面的循环，在这里直接拦截返回
        if length_chain == 0:
            # 如果本身就是空链表，直接返回false
            return False
        if length_chain == 1:
            if current_node.data == item:
                return True
        while current_node is not None:
            if current_node.data == item:
                return True
            # 把每个节点的next重新赋值给current_node，继续下一层循环
            current_node = current_node.next
        return False

再附上实现链表数据结构，匹配的测试用例。这代码写得简直越来越专业了呢！

"""
测试用例，单向链表。
"""
import unittest

from chain_demo import ChainNode, ChainList


class ChainTest(unittest.TestCase):
    def setUp(self):
        """init the original node and chain object"""
        node = ChainNode(30)
        self.chain = ChainList(node)

    def test_len(self):
        """test get length of chain"""
        length_chain = self.chain.length()
        self.assertEqual(length_chain, 1)
        # test length of empty chain
        chain_ = ChainList()
        empty_chain_len = chain_.length()
        self.assertEqual(empty_chain_len, 0)

    def test_travel(self):
        """test show all chain"""
        nodes_li = self.chain.travel()
        self.assertIn(30, nodes_li)

    def test_add(self):
        """test add chain"""
        self.chain.add(20)
        nodes_li = self.chain.travel()
        self.assertEqual(nodes_li, [20, 30])

    def test_append(self):
        """test append chain"""
        self.chain.append(40)
        self.chain.append(55)
        self.chain.insert(1, 35)
        # self.chain.insert(0, 35)
        nodes = self.chain.travel()
        self.assertIn(40, nodes)
        # 测试用例方法，彼此之间没有强绑定关系，虽然上面已经有add一个节点了，
        # 但是这边append的结果并没有带上add的结果，彼此是独立的，内存空间并不会共享
        # self.assertEqual(nodes, [35, 30, 40, 55])
        self.assertEqual(nodes, [30, 35, 40, 55])

    def build_original_test_data(self):
        """build original data to the chain for search and remove test"""
        self.chain.add(20)
        self.chain.append(3)
        self.chain.append(33)
        self.chain.append(13)

    def test_search(self):
        """test search node and remove node"""
        self.build_original_test_data()
        nodes = self.chain.travel()
        for i in nodes:
            search_result = self.chain.search(i)
            self.assertTrue(search_result)

    def test_remove(self):
        """test remove node"""
        self.build_original_test_data()
        nodes = self.chain.travel()
        print("before-remove>>>", nodes)
        self.chain.remove(3)
        self.chain.remove(13)
        self.chain.remove(20)
        nodes = self.chain.travel()
        print("after-remove>>>", nodes)
        self.assertNotIn(3, nodes)
        self.assertNotIn(13, nodes)


unittest.main()

 

 

树

树是二维图形。

树形结构有很多种，二叉树，完全二叉树，红黑树，平衡树。

树是不可逆的，从树顶到树枝末端，是一个从上到下的过程，不能返回。

 

图

图是二维图形。

图是可逆的，这一点上是针对树结构来说的。