day15 函数的使用方法：递归函数

这里归纳的知识点主要就是：

浮点数，复数，

int，整形；float，浮点数；complx，复数；

 

# 实数：
    # 有理数  有限小数     1.2
    #         无限循环小数  1.23232323232323.....
    # 无理数  无限不循环小数
#浮点数-小数
#浮动
#1.2 = 12*0.1
#1.2 = 0.12*10

# py2和3的区别
# print(1/2)

#浮点数的特点
# a = 1.15346974071908269370703493
# print(a)

#float
# print(float('1.234'))

#复数   a+bj   实部+虚部
#  实数 ：1
#  虚数 ：j
#平方是-1的数就是j
"-1"
#复数：
# 复数之间不能比较大小
# 2+3j
# 2+3J
# complex

 

 

 

递归函数

初识递归：

 

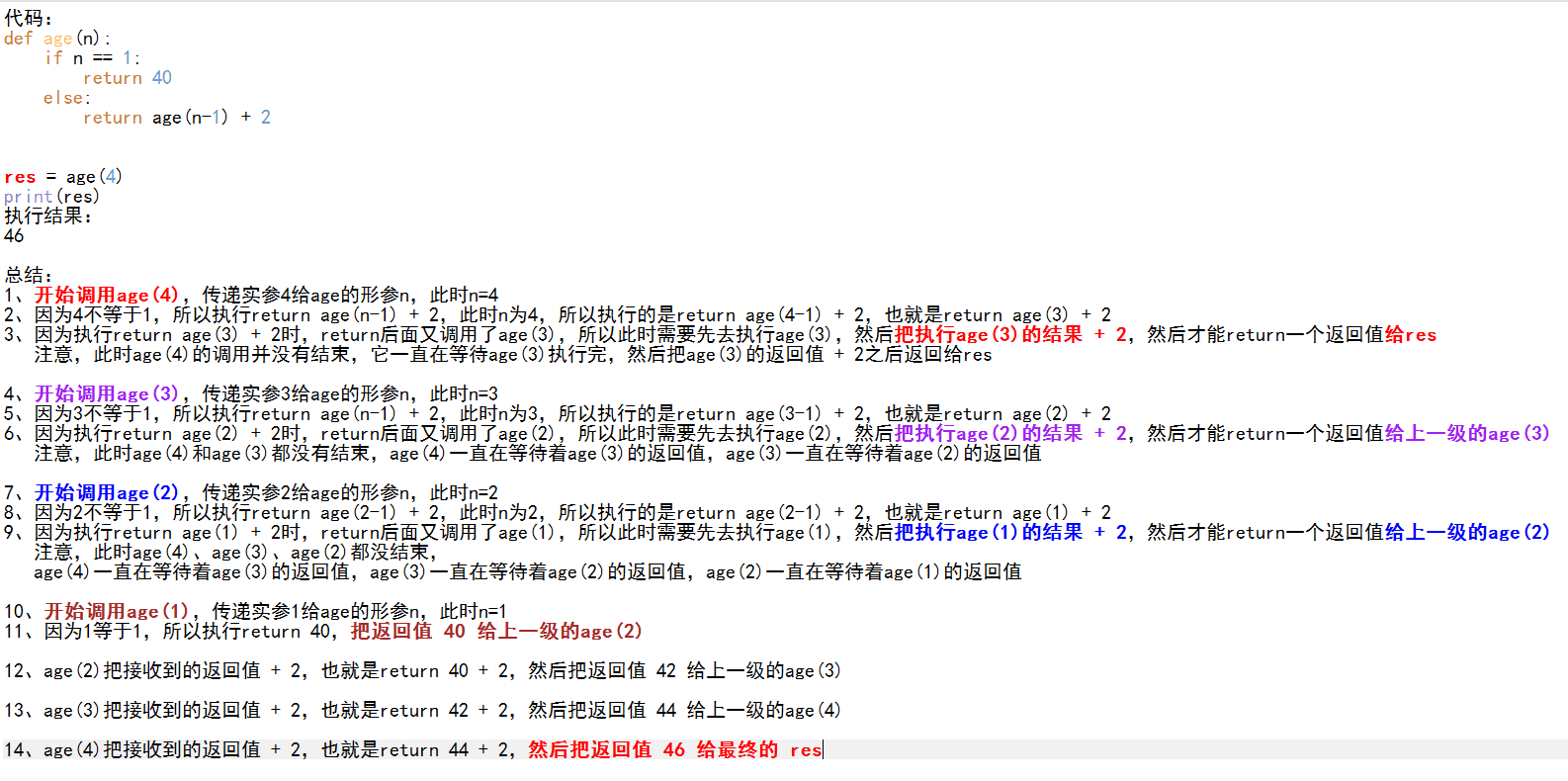
# def story():
#     print('从前有座山，山里有座庙，庙里有个老和尚讲故事，讲的什么呢？')

#功能解耦：
#为什么要有函数：提高代码可读性，避免重复的代码，提高代码的复用性
#在函数中能return的不要print
# while True:
#     story()

# def story():
#     print('从前有座山，山里有座庙，庙里有个老和尚讲故事，讲的什么呢？')
#     story()
#
# story()
# import sys
# # print(sys.getrecursionlimit())
# sys.setrecursionlimit(2000000000)
# n = 0
# def func():
#     global n
#     n+=1
#     print(n)
#     func()
# func()

#递归
#在一个函数里面 调用 自己
#默认的递归最大限度 1000
#不要修改默认的递归最大限度
#往往 递归 都是 和循环挂在一起的
# 人理解循环 神理解递归
# 算法，递归函数
# 认识递归
# 递归函数怎么读？
# 带着你写两段代码

#多大了alex，我不告诉你，alex比egon大两岁    44+2
#egon多大了，我不告诉你，egon比wusir大两岁   42+2
#wusir多大了，我不告诉你，wusir比金鑫大两岁  40+2
#金鑫40了

# age(1) n = 1 age(2)+2
# age(2) n = 2 age(3)+2
# age(3) n = 3 age(4)+2
# age(4) n = 4 40

def age(n):
    if n == 4:
        return 40
    return age(n+1)+2

print(age(0))

# def age(0):
#     if n == 4:
#         return 40
#     return age(1)+2               #48

# def age(1):
#     if 1 == 4:
#         return 40
#     return age(2)+2                #46   这个46返回给上面的return age(1)+2
#
# def age(2):
#     if 2 == 4:
#         return 40
#     return age(3)+2         # 44　　　这个４４返回给上面的return age(2)+2
#
# def age(3):
#     if 3 == 4:
#         return 40
#     return age(4)+2    #return 42　　这个４２返回给上面的return age(3)+2
#
# def age(4):
#     if 4 == 4:
#         return 40     这个４０返回给上面的return age(4)+2
#     # age(n+1)+2

 

 

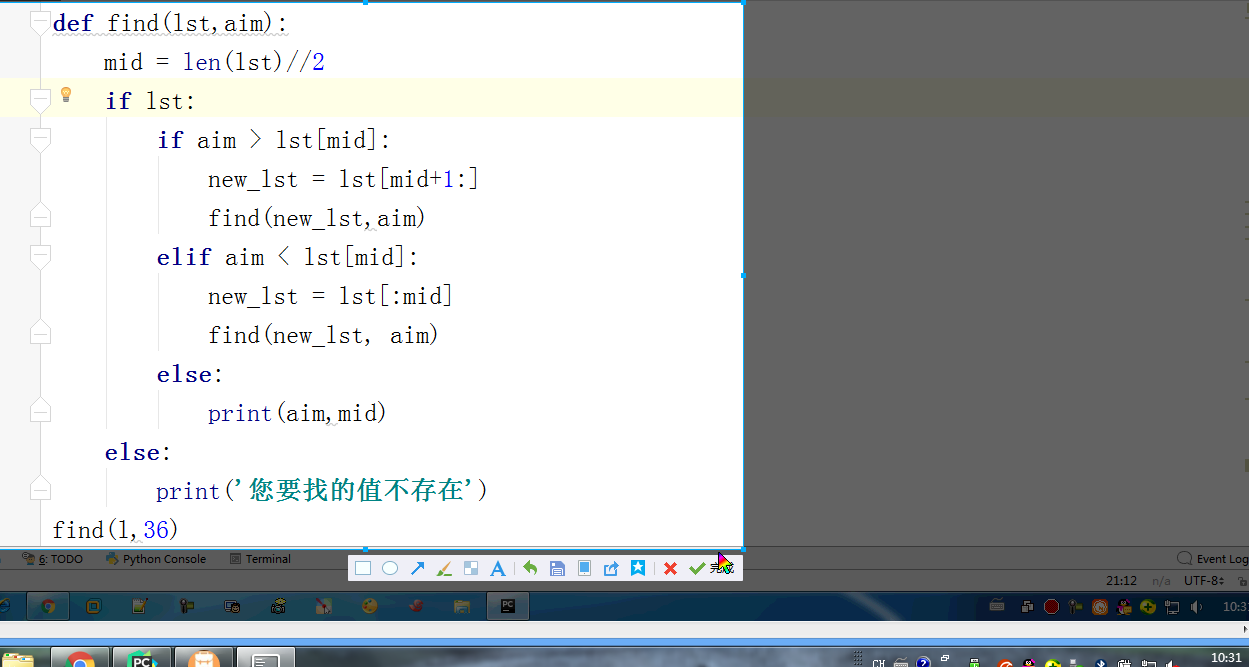
二分查找算法：

def dichotomy(l, target, start=0, end=None):
    """
    二分查找，递归
    :param l:
    :param target:
    :param start:
    :param end:
    :return:
    """
    if end is None:
        end = len(l)-1
    if start <= end:
        mid = (end-start)//2+start
        if l:
            if target > l[mid]:
                r = dichotomy(l, target, mid+1, end)
            elif target < l[mid]:
                r = dichotomy(l, target, start, mid)
            else:
                return mid
        else:
            return None
        return r


ll = [2, 4, 5, 7, 9, 12, 36]
rr = dichotomy(ll, 36)
print(rr)

 

 

阶乘算法，斐波那契数列算法：

#阶乘的计算
#什么叫阶乘： 7  #7*6*5*4*3*2*1

def f(n):
    if n == 1:
        return 1
    else:
        return n*f(n-1)

# f(3)

#斐波那契数列
# 1,1,2,3,5,8,13....
# n = 10
# f(10) = f(8)+f(9)
def fib(n):
    if n == 1 or n == 2:
        return 1
    return fib(n-1)+fib(n-2)

print(fib(6))

####本来会斐波那契了，这样把递归函数套进来，然后就不会了。。。。好难理解啊，怎么这么绕啊

 

 我居然自己搞明白了！我简直太牛逼了！

这是我自己推导的斐波那契数列的思路

# 斐波那契数列：
def fib(n):
    if n == 1 or n == 2:
        return 1
    return fib(n-1) + fib(n-2)
fib(n)
#n=8
def fib(8):#所以fib（8）就是21
    if n == 1 or n == 2:
        return 1
    return fib(8-1) + fib(8-2)#这里fib（7）+fib（6）最终return的结果是21
#请注意要从下往上看！！！！
# 此时需要把return fib（8-1）和fib（8-2）的函数分别求出return的值，然后相加就可以得到fib（8）的值
# 那么fib（8-1）就是fib（7），同理，fib（8-2）就是fib（6）
# 现在我们来分别求出fib（7）的值和fib（6）的值。其实很简单的，就是过程很麻烦重复很多遍，要不断的向下去求值。
# 要求fib（6）的值就把它放进上面的函数公式里即可一层层剥皮得到最下层的结果，再一层层加上来，就实现了递归。
# 开始执行：
def fib(7):#所以fib（7）就是13
    if n == 1 or n == 2:
        return 1
    return fib(7-1)+fib(7-2)#这里fib（6）+fib（5）最终return的结果是13
def fib(6):#所以fib（6）就是8
    if n == 1 or n == 2:
        return 1
    return fib(6-1)+fib(6-2)#这里fib（5）+fib（4）最终return的结果是8
def fib(5):#所以fib（5）就是5
    if n == 1 or n == 2:
        return 1
    return fib(5-1)+fib(5-2)#这里fib（4）+fib（3）最终return的结果是5
def fib(4):#所以fib（4）就是3
    if n == 1 or n == 2:
        return 1
    return fib(4-1)+fib(4-2)#这里fib（3）+fib（2）最终return的结果是3
def fib(3):#所以fib（3）就是2
    if n == 1 or n == 2:
        return 1
    return fib(3-1)+fib(3-2)   #这里fib（2）+fib（1）最终return的结果是2
def fib(2):
    if n == 1 or n == 2:
        return 1   #我们一层一层剥下来，这里就是最底层，现在开始向上一层一层相加

 另一种实现方式

def fib():
    a = 1
    b = 2
    while True:
        c = a + b
        yield c
        a = c + b
        yield a
        b = a + c
        yield b


obj = fib()
print(next(obj))
print(next(obj))
print(next(obj))
print(next(obj))
print(next(obj))
print(next(obj))
print(next(obj))

 

 

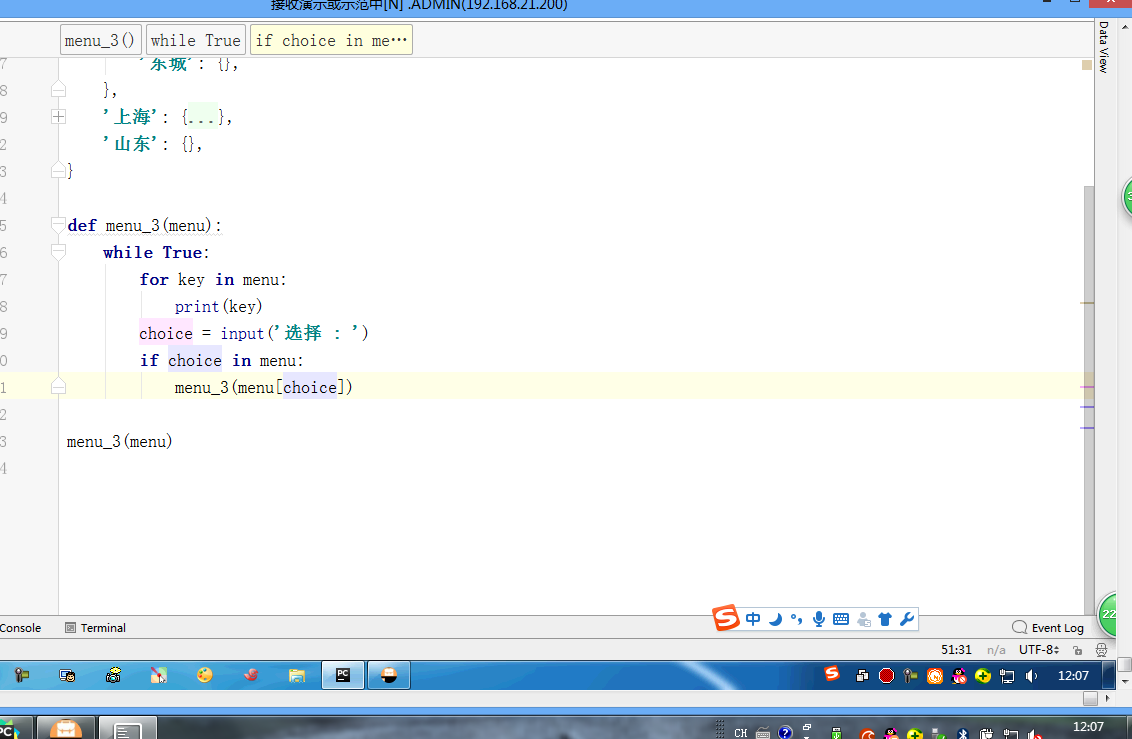
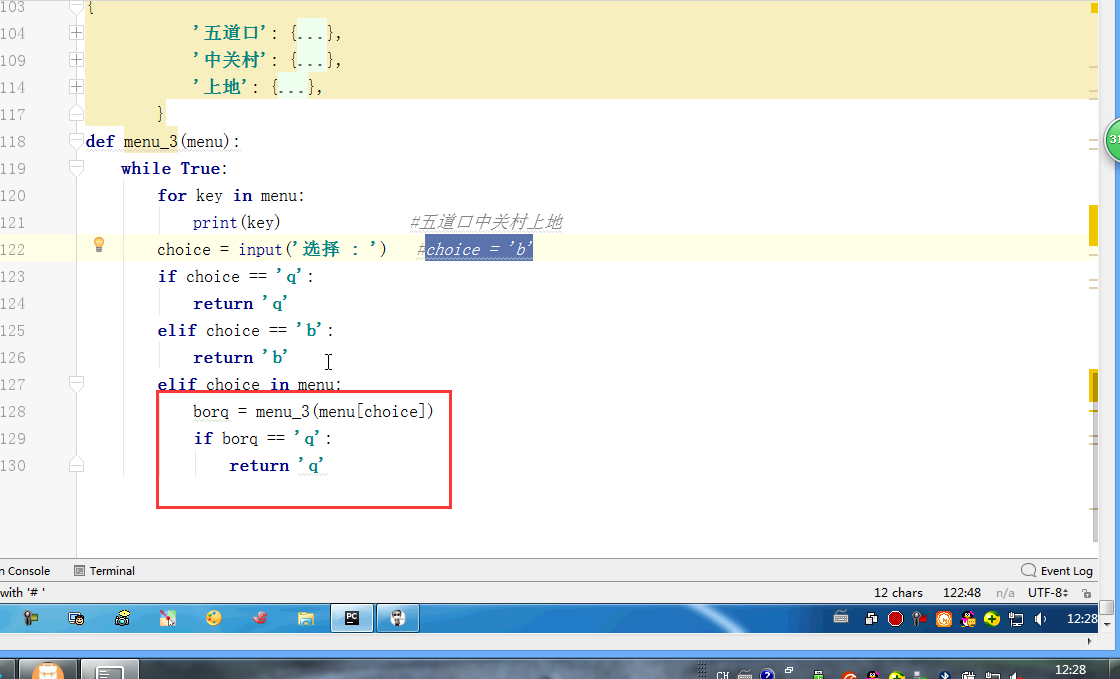
三级菜单的递归函数：

menu = {
    '北京': {
        '海淀': {
            '五道口': {
                'soho': {},
                '网易': {},
                'google': {}
            },
            '中关村': {
                '爱奇艺': {},
                '汽车之家': {},
                'youku': {},
            },
            '上地': {
                '百度': {},
            },
        },
        '昌平': {
            '沙河': {
                '老男孩': {},
                '北航': {},
            },
            '天通苑': {},
            '回龙观': {},
        },
        '朝阳': {},
        '东城': {},
    },
    '上海': {
        '闵行': {
            "人民广场": {
                '炸鸡店': {}
            }
        },
        '闸北': {
            '火车战': {
                '携程': {}
            }
        },
        '浦东': {},
    },
    '山东': {},
}

def menu_3(menu):
    while True:
        for key in menu:
            print(key)      #北京上海山东
        choice = input('选择 : ')   #北京
        if choice == 'q' or choice == 'b':
            return choice
        elif choice in menu and menu[choice]:        #北京 in menu
            borq =  menu_3(menu[choice])
            if borq == 'q':
                return 'q'

menu_3(menu)