图总结

一.思维导图

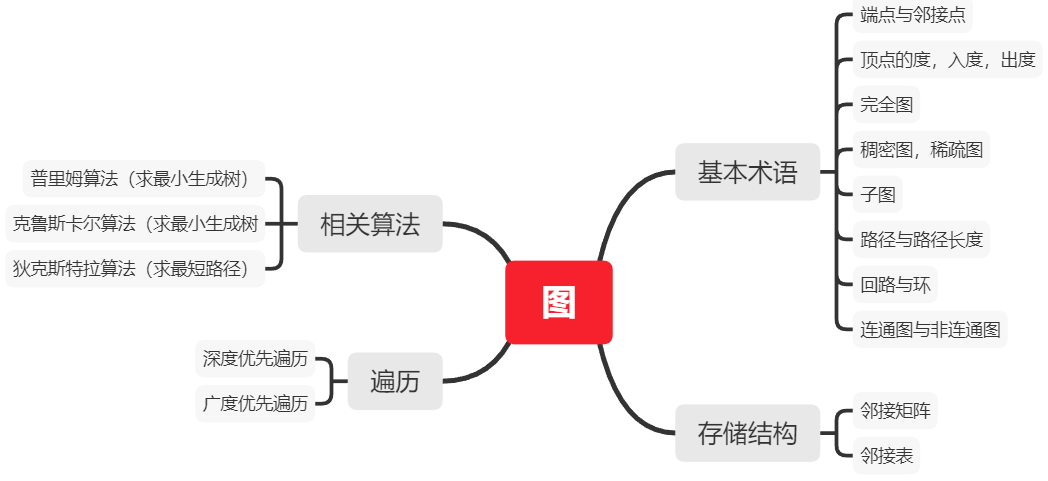
二.重要概念

1.深度优先遍历（DFS）

类似于树的先根遍历

void DFSTraverse(MGraph G)
{ 
    int v;  
    for( v = 0; v < G.vexnum; ++v) visited[v] = false;  
    for( v = 0; v < G.vexnum; )   
        if(!visited[v]) DFS( G, v); 
        ++v; 
  
}  

2.广度优先遍历（BFS）

类似于树的层次遍历

void BFSTraverse(MGraph G)  
{  
    Queue Q;  
    int u;  
    for(int m=1; m<= G.vexnum; m++) visited[m] = false;  
    InitQueue(Q);  
    for(int v=1;v<=G.vexnum;v++)  
        if(!visited[v]) {  
            visited[v]=true;  
            visitVex(G,v);  
            EnQueue(Q,v);  
            while(Q.len!=0)  
            {  
                DeleteQueue(Q,u);  
                for(int w=FirstAdjVex(G,u);w>=1;w=NextAdjVex(G,u,w))  
                    if(!visited[w])  
                    {  
                        visited[w]=true;  
                        visitVex(G,v);  
                        EnQueue(Q,w);  
                    }  
            }  
        }  
        cout<<endl;  
}  

3.普里姆算法与克鲁斯卡尔算法（求最小生成树）

普里姆算法从顶点的角度为出发点，时间复杂度为O（n^2),适合于解决稠密图；克鲁斯卡尔算法从边的角度出发，时间复杂度为O（nlogn),适合于解决稀疏图。

4.拓扑排序

用于判断一个有向图有无环，执行步骤为

(1) 选择一个入度为0的顶点并输出之；

(2) 从网中删除此顶点及所有出边。

直到不存在入度为0的顶点为止。

三.疑难问题及解决方法

1.问题：不理解拓扑排序

解决方法：熟知拓扑排序步骤

• 从DGA图中找到一个没有前驱的顶点输出。(可以遍历，也可以用优先队列维护)

• 删除以这个点为起点的边。(它的指向的边删除，为了找到下个没有前驱的顶点)

• 重复上述，直到最后一个顶点被输出。如果还有顶点未被输出，则说明有环！

  例如以下有向无环图，求其拓扑排序序列
  

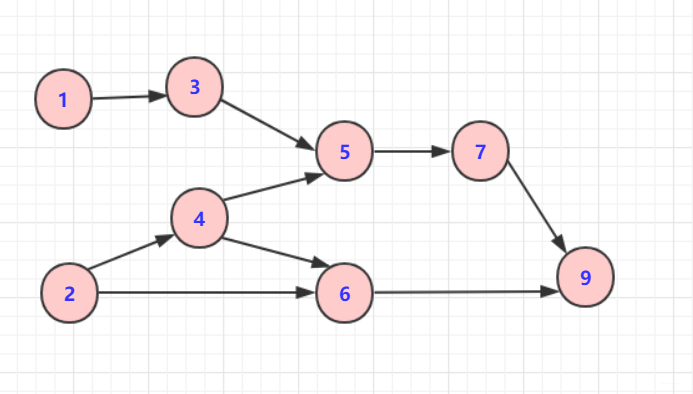
  1.删除1或2输出

  2.删除2或3以及对应的边

  3.删除3或4以及对应的边

  重复以上步骤得到最终拓扑排序序列为1 2 4 3 6 5 7 9（序列不唯一）