201971010115-蒋敏敏 实验二 个人项目—0/1背包问题项目实战
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 2019级卓越工程师班 |
| 这个作业要求链接 | 实验二 软件工程个人项目 |
| 我的课程学习目标 | 1. 掌握个人软件项目开发流程 2. 掌握GitHub发布项目的操作方法 3. 阅读一些算法书籍 |
| 这个作业在哪些方面帮助我实现学习目标 | 1. 通过0/1背包问题这一项目,熟悉了个人软件项目开发流程 2. 掌握GitHub发布项目的操作方法 3. 更加熟悉了三种算法的应用 |
| 项目Github的仓库链接地址 | 仓库地址 |
任务1:阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中本次已提交作业至少3份。
1. 源代码管理工具与开发工具
- 本次开发使用Python开发,开发环境为PyCharm,用于整个程序的开发。使用GitHub项目管理工具上传项目,还用到了WPS绘制流程图和功能图。
2. 点评班级博客链接
任务2:总结详细阅读《构建之法》第1章、第2章,掌握PSP流程。
1. 第一章:总结了如下知识点
1.1 软件=程序+软件工程
(1) 程序=数据结构+算法
程序,就是指的源程序,是可执行代码。软件构建,构建成机器能懂的可执行代码,要有合理的软件架构,软件设计与实现,还要有各种文件和数据来描述各个程序文件之间的依赖关系,编译参数,链接参数等等。
软件工程是把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程。软件工程的核心部分:项目管理、源代码管理、软件需求分析、软件设计、软件构建管理、软件测试和软件维护(服务运营)等。
(2) 软件企业=软件+商业模式
程序(算法、数据结构)是基本功,但是在算法和数据结构之上,软件工程决定了软件的质量;商业模式决定了软件企业的成败。软件从业人员和软件企业的道德操守会极大地影响软件用户的利益。
1.2 软件开发的不同阶段
(1) 玩具阶段:写程序联系数据结构/算法
(2) 业余爱好阶段:用JavaScript等写写网站
(3) 探索阶段:专研新技术,应用新技术在软件行业创新
(4) 成熟的产业阶段:开发软件/操作系统
2. 第二章:单元测试,回归测试,效能分析,个人软件开发流程(PSP)。
-
2.1 单元测试
软件是由多人合作完成的,不同人员的工作相互有依赖关系。单元测试是模块质量稳定和量化的保证。
-
2.2 回归测试
从正常工作的稳定状态退化到不正常工作的不稳定状态。
其目的是:验证新的代码的确修改了缺陷;同时验证新的代码有没有破坏模块的现有功能,有没有Regression。
单元测试是回归测试的基础。
-
2.3 效能分析工具
就是为了让我们能很快地找到程序的效能瓶颈,改进程序。
方法一:抽样(当程序运行的时候,时不时看一看这个程序运行在哪一个函数内,并记录下来。)
方法二:代码注入(是将检测的代码加入到每一个函数中,这样的程序一举一动都会被记录在案,程序的各个效能数据都可以被精确地测量。)
-
2.4.个人开发流程
(1)计划(估计这个任务需要多少时间)
(2)开发(包括 分析需求,生成设计文档,设计复审(和同事审核设计文档),代码规范(为目前的开发定制合适的规范),具体设计,具体编码,代码复审,测试(包括自测,修改代码,提交修改))
(3)记录用时
(4)测试报告
(5)计算工作量
(6)事后总结
(7)提出过程改进计划
-
2.5.PSP特点
(1)不局限于某一个软件技术,而是着眼于软件开发的流程,这样开发不同应用的软件工程师可以相互比较。
(2)不依赖与考试,而主要靠工程是自己手机数据,然后分析,提高。
(3)PSP依赖于数据,需要工程师输入数据,记录工程师的各项活动,再加上数据不准确或者有遗失。
(4)PSP的目的记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度。
-
2.6.PSP作用
PSP可以帮助软件工程师在个人的基础上运用过程的原则,借助于PSP提供的一些度量和分析工具,了解自己的技能水平,控制和管理自己的工作方式,使自己日常工作的评估、计划和预测更加准确、更加有效,进而改进个人的工作表现,提高个人的工作质量和产量,积极而有效地参与高级管理人员和过程人员推动的组织范围的软件工程过程改进。
任务3:项目开发
1. 项目内容
从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
2. 需求分析
-
读入文件数据:
正确读入实验数据文件的有效{0-1}KP数据。 -
绘制散点图:
绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图。 -
排序:
能够对一组{0-1}KP数据按重量比进行非递增排序。 -
算法
用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位); -
结果存入文件
任意一组{0-1} KP数据的最优解、求解时间和解向量可保存到txt文件。 -
扩展功能
- 绘制以单位价值为横轴,物品序号为纵轴的柱状图
- 可以将绘制的散点图和柱状图保存到一个文件夹中
3. 功能设计
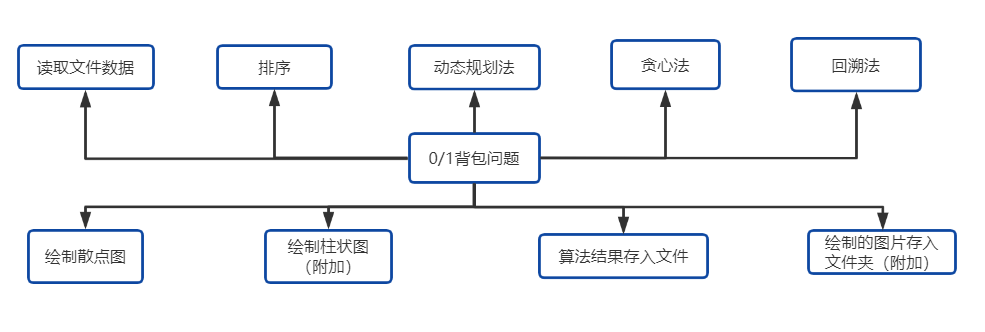
4. 设计实现
4.1 系统运行过程如下:
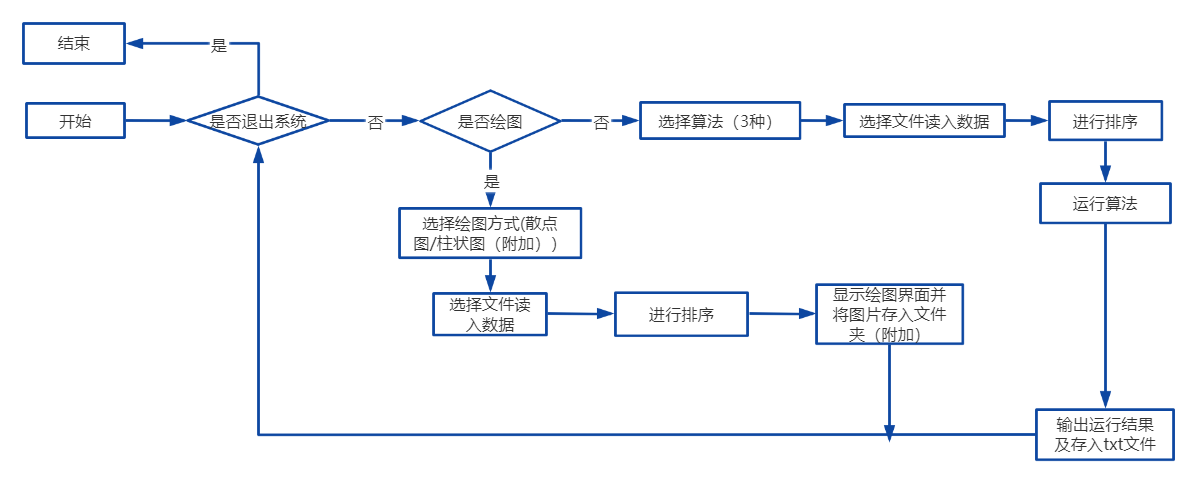
4.2 读入数据:读取文件数据,做好准备工作。
4.3 算法:
-
动态规划法:
bag()函数:找出状态转移方程,进行填表操作,得出最优解,算法的时间复杂度为O(nm)。 -
贪心法:
vw()函数和sort()函数:计算单位重量的价值并进行递减排序。
Greedy()函数:依次装入排序后的物品,得到的是近似解,算法的时间复杂度为O(n)。 -
回溯法:
backtrack()函数:遍历解空间,找出最优解,算法的时间复杂度为O(n!)。
4.4 存入文件:
- 算法结果存入:每次算法运行都会将计算出的最优解,耗费时间,解向量次存入result.txt文件。
- 图的存入:存入src文件夹中,方便查看。
5. 代码规范
| 项目 | 规则 |
|---|---|
| 缩进 | 用4个空格来缩进代码 |
| 变量命名 | 变量名尽量小写, 如有多个单词,用下划线隔开 |
| 每行最多字符数 | 每行不超过80个字符 |
| 函数最大行数 | 单个函数行数限制不超过100行 |
| 函数、类命名 | 1. 模块尽量使用小写命名,首字母保持小写,尽量不要用下划线; 2. 类名使用驼峰(CamelCase)命名风格,首字母大写,私有类可用一个下划线开头; 3. 函数名一律小写,如有多个单词,用下划线隔开 |
| 常量 | 常量使用以下划线分隔的大写命名 |
| 空行规则 | 1. 模块级函数和类定义之间空两行; 2. 类成员函数之间空一行; |
| 注释规则 | 1. “#”号后空一格,段落间用空行分开(同样需要“#”号); 2. 不要在文档注释复制函数定义原型, 而是具体描述其具体内容, 解释具体参数和返回值等 |
| 操作符前后空格 | 在二元运算符两边各空一格[=,-,+=,==,>,in,is not, and]: |
6. 代码展示
读取文件数据
daten = open(str, "r")
lines = daten.readlines()
list = []
for i in lines:
list.append(i.strip().split(' '))
daten.close() daten = open(str, "r")
动态规划法
def bag(n, c, w, v, s, last_time):
# 置零,表示初始状态
value = [[0 for j in range(c + 1)] for i in range(n + 1)]
for i in range(1, n+1):
for j in range(1, c+1):
value[i][j] = value[i - 1][j]
# 背包总容量够放当前物体,遍历前一个状态考虑是否置换
if j >= w[i - 1] and value[i][j] < value[i - 1][j - w[i - 1]] + v[i - 1]:
value[i][j] = value[i - 1][j - w[i - 1]] + v[i - 1]
print("最大价值为:", value[i][j])
j = c
i = n
y1 = [0 for i in range(1, n+1)]
while i != 0:
if value[i][j] > value[i-1][j]:
y1[i-1] = 1
j = j-w[i-1]
else:
y1[i-1] = 0
i = i-1
print("解向量为:", y1)
贪心法
for i in range(n):
if w[y[i]-1] + weight < c:
value += v[y[i]-1]
weight += w[y[i]-1]
z[y[i]-1] = 1
else:
z[y[i]-1] = 0
print("最大价值为:", value)
print("解向量为:", z)
回溯法
def backtrack(i, w, v, n, c, x):
global bestV, curW, curV, bestx
# 若找到一个可行解,比较当前总价值与已得到的最大价值比较,若大于,则进行替换,否则,继续寻找下一个解,直到遍历结束
if i >= n:
if bestV < curV:
bestV = curV
bestx = x[:]
else:
if curW+w[i] <= c:
x[i] = 1
curW += w[i]
curV += v[i]
backtrack(i+1, w, v, n, c, x)
curW -= w[i]
curV -= v[i]
x[i] = 0
backtrack(i+1, w, v, n, c, x)
绘制散点图
colors = 'red' # 点的颜色
area = np.pi * 2**2 # 点面积
# for i in range(len(w)):
plt.scatter(w, v, s=area, c=colors, alpha=0.1, label=' ')
plt.legend()
plt.yticks(())
plt.title('散点图')
plt.savefig('./src/scatter.jpg') # 保存图片
plt.show()
y_pos = np.arange(len(w))+1
ax.barh(y_pos, y, color='b', align="center")
plt.savefig('./src/barh.jpg') # 保存图片
plt.show()
结果存入txt文件
file_handle = open('result.txt', mode='a')
file_handle.write(s)
file_handle.write(' 解向量:[')
for i in z:
file_handle.write(str(i))
file_handle.write(',')
file_handle.write('] 耗时:')
file_handle.write(str(current_time - last_time))
file_handle.write('\n')
file_handle.close()
plt.savefig('./src/scatter.jpg') # 保存图片
plt.savefig('./src/barh.jpg') # 保存图片
7. 测试运行
- 主界面:
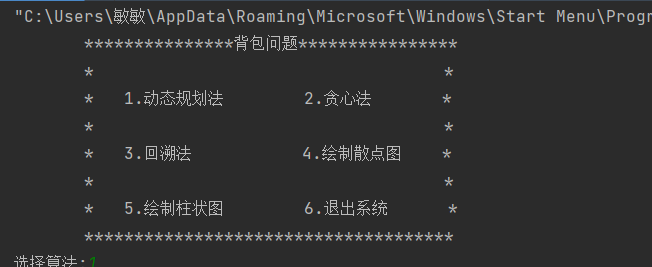
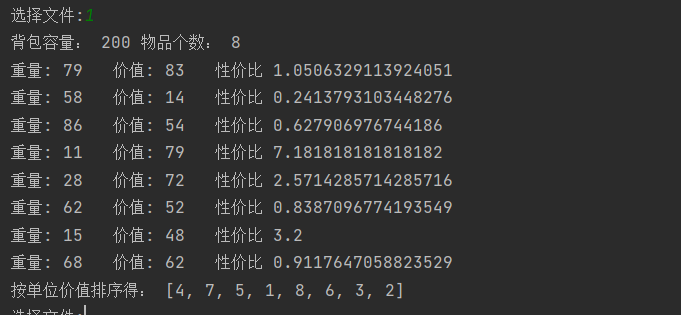
- 进入算法示例:

- 按重量比进行非递增排序:
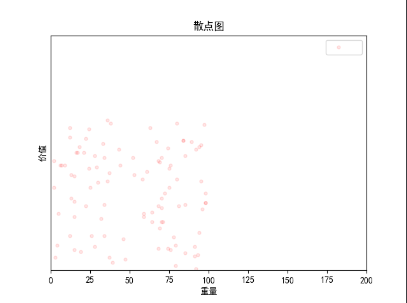
- beibao5.in的散点图:
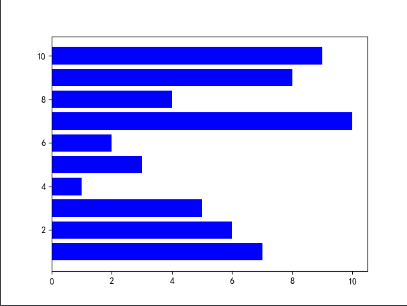
- beibao2.in的柱状图:以单位重量价值为横轴,物品序号为纵轴
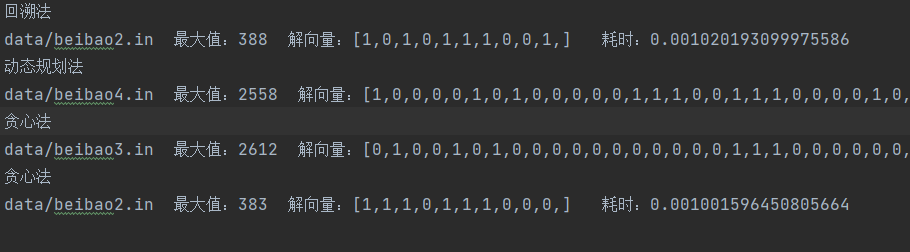
- 算法结果存入文件:
- 散点图和柱状图存入文件夹:
8. 总结
本次项目采用模块化设计思想,每部分功能用函数封装,方便调用,易于改动,模块间相互独立,只需要改变参数即可。例如,贪心法在函数Greedy()中实现,动态规划法在bag()函数中实现,回溯法在backtrack()函数中实现,独立执行自身的功能,互不干扰。在实现动态规划法的时候遇到了点困难,逻辑上有点混乱,最后在网站上看了别人的讲解视频,才解决了这个问题。最后就是对Markdown的编写不是很熟悉,导致写报告花费时间较多。
9. PSP展示
| PSP2.1 | 任务内容 | 计划完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 10 | 8 |
| -Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 10 | |
| Development | 开发 | 480 | 460 |
| - Analysis | - 需求分析(包括学习新技术) | 12 | 8 |
| - Design Spec | - 生产设计文档 | 6 | 7 |
| - Design Review | - 设计复审(和同事审核设计文档) | 6 | 5 |
| - Coding Standard | - 代码规范(为目前的开发指定合适的规范) | 6 | 7 |
| - Design | - 具体设计 | 10 | 12 |
| - Coding | - 具体编码 | 240 | 250 |
| - Code Review | - 代码复审 | 20 | 15 |
| - Test | - 测试(自我测试,修改代码,提交修改) | 60 | 70 |
| Reporting | 报告 | 50 | 50 |
| - Test Report | - 测试报告 | 20 | 15 |
| - Size Measurement | - 计算工作量 | 20 | 15 |
| - Postmortem & Process Improvement Plan | - 事后总结,并提出过程改进计划 | 16 | 14 |
任务4:完成任务3的程序开发,将项目源码的完整工程文件提交到你注册Github账号的项目仓库中。