第三届里奇杯编程大赛(决赛)题解
A.砍价
把原本需要付的钱记录下,减去老板优惠掉的那部分钱就可以。
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
// sum 记录商品价格总和
// maxv 记录最贵商品的价格
int n, sum = 0, maxv = 0;
scanf("%d", &n);
for(int i=1; i<=n; i++) {
int p; scanf("%d", &p);
sum += p;
maxv = max(maxv, p);
}
printf("%d\n", sum - maxv/2);
return 0;
}
B.鸡兔同笼
枚举鸡的数量为 \(i(0 \le i \le X)\) ,判断 \(2i + 2(X - i)\) 是否等于 \(Y\) 即可。
#include <iostream>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int m, n, q;
int f[N];
vector <pair<int,int> > e[N];
void solve()
{
cin >> n >> m;
bool flag = false;
for(int i = 0; i <= n; i ++)
{
int j = n - i;
if(i * 2 + j * 4 == m) flag =true;
}
if(flag) cout << "Yes";
else cout << "No";
}
int main()
{
// 取消同步,加快cin,cout的速度(不能与scanf/printf混用)
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
C.跳石头
经典线性动态规划(DP)。设定 \(f_i\) 表示当机器人在第 \(i\) 块石头上的时候,整个过程最少要消耗的能量。
转移方程为 \(f_i = min\{f_{i-2} + |h_i - h_{i-2}|, f_{i-1} + |h_i - h_{i-1}|\}\) 。表示判断 \(f_i\) 从 \(f_{i-2}\) 转移过来为最优解,还是从 \(f_{i-1}\) 转移过来为最优解。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, a[N], f[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
}
// f[1] = 0
// 2 没有 0(i-2) 个石头,只能从第 1 个石头转移过来
f[2] = abs(a[2] - a[1]);
for(int i = 3; i <= n; i ++)
{
f[i] = min(f[i - 1] + abs(a[i - 1] - a[i]), f[i - 2] + abs(a[i - 2] - a[i]));
}
// 根据定义,f[n] 为机器人在第 n 块石头上的时候,整个过程最少要消耗的能量,故为答案
cout << f[n];
return 0;
}
D.生存还是毁灭
假如可以买 \(i\) 个草莓,那么一定满足
在坐标图中 \(f(x) = i \times x\) 表示如下,横轴表示购买草莓的质量,纵轴表示购买草莓总和的质量,斜率表示购买草莓的数量。
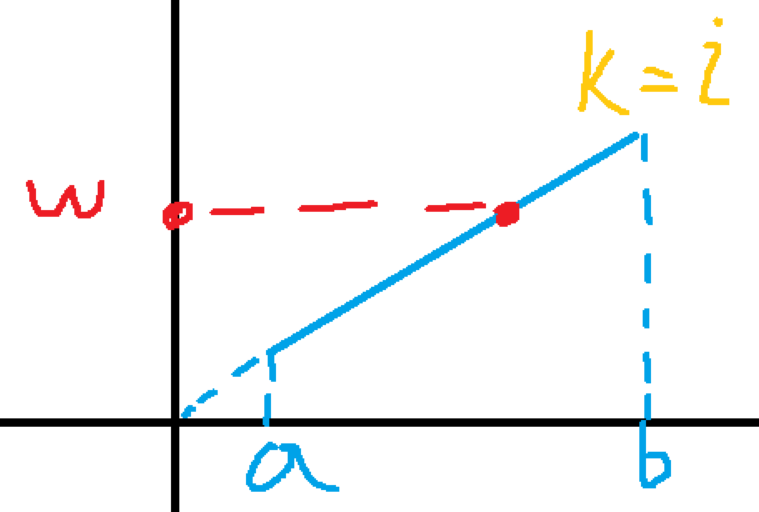
当 \(i\) 变大,也就是斜率变大时,直线会绕着原点在第一象限逆时针旋转,会存在一个值 \(i_{max}\), 当 $ i \gt i_{max}$ 时,会使得 \(i \times a \gt w\),不符合要求。反之,存在一个值 \(i_{min}\), 当 $ i \lt i_{min}$ 时,会使得 \(i \times a \lt w\),不符合要求。我们所要求的就是 \(i_{max}, i_{min}\)。
可以用列式子直接算出来,也可以枚举 \(i\) 判断符不符合条件来记录结果。
// 枚举i写法
#include <iostream>
using namespace std;
int main() {
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
w *= 1000;
int maxv = 0, minv = 1e9;
for(int i=1; i<=1e6; i++) {
if(a*i <= w && b*i >= w) {
maxv = max(maxv, i);
minv = min(minv, i);
}
}
if(!maxv) puts("not to be\nrun");
else printf("to be\n%d %d\n", minv, maxv);
return 0;
}
// 直接求写法
#include <iostream>
using namespace std;
int main() {
int a, b, w;
cin >> a >> b >> w;
w *= 1000;
int maxv = (w+a-1)/a, minv = w/b;
if(maxv-minv <= 1 && w < a*maxv && w > b*minv) {
puts("not to be\nrun");
return 0;
}
if(w < a * maxv) maxv--;
if(w > b * minv) minv++;
printf("to be\n%d %d\n", minv, maxv);
return 0;
}
E.完美X序列
当把一个序列 \(a\) 变为完美 \(x\) 序列时,所有的 \(a_i (a_i < x)\) 都要加上 \(x - a_j\) 的值,所有 \(a_j (a_j > x)\) 都要减去 \(a_j - x\) 的值。
故我们把问题转换成了如何找到比 \(x\) 小的值和比 \(x\) 大的值。可以通过排序,把序列 \(a\) 变为非递减序列。这样只要在序列中找到 \(x\) ,那么左边的数都比它小,右边的数就都比它大。
那找到比 \(x\) 小/大的数了,如何快速求出需要加/减的值?可以通过前缀和在 \(O(1)\) 复杂度下求出。
找 \(x\) 的过程可以使用二分,复杂度为 \(O(\log_2n)\) 。
程序总体复杂度为为 \(O(n + n \log_2n + q \log_2n)\) 约为 \(O(n \log_2n)\) 即 \(2 \times 10^5 * \log_2{(2 \times 10^5)} \approx 3.6 \times 10^6 \le 10^8\) 稳过。
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
long long n, q, a[N], s[N];
int main()
{
cin >> n >> q;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
}
// 排序
sort(a + 1, a + n + 1);
// 求前缀和
for(int i = 1; i <= n; i ++)
{
s[i] = s[i - 1] + a[i];
}
while(q --)
{
int x;
cin >> x;
int l = 0, r = n;
// 二分找到 <=x 的最大的数
while(l < r)
{
int mid = l + r + 1 >> 1;
if(a[mid] <= x) l = mid;
else r = mid - 1;
}
long long res = 0;
// 左边需要加的次数
res += (long long)l * x - s[l];
// 右边需要减的次数
res += s[n] - s[l] - (long long)x * (n - l);
cout << res << '\n';
}
return 0;
}
F.DDL战神
两个人去写作业,最快完成作业所需要的时间是 \(\frac{sum}{2}\) ,\(sum\) 指的是所有作业时间之和。大部分情况下,不能把作业分别分配给2个人使得每个人作业时间恰好为 \(\frac{sum}{2}\) 。
故大多数情况是其中一个人的作业时间 \(sum_1 \ge \frac{sum}{2}\) , 另一个人的作业时间 \(sum_2 \le \frac{sum}{2}\) 。
要让答案最小,也即是使得 \(max\{ sum_1, sum_2 \} = sum_1\) 最小,即让 \(sum_2\) 在满足条件的状况下尽可能最大。
此时问题就转换为了经典的01背包问题:从 \(n\) 个作业中选,在满足作业的时间 \(sum_2 (sum_2 \le \frac{sum}{2})\) 的情况下,选到的价值尽可能的大。这里背包的体积是 \(\frac{sum}{2}\) ,作业的价值等同于时间。
设 \(f_{i,j}\) 为当选到第 \(i\) 个作业,作业时间之和为 \(j\) 时,价值最高为多少。转移方程是 \(f_{i,j} = max\{ f_{i-1,j}, f_{i-1,j-a_i}+w_i \}\) 。
由于当选到第 \(i\) 个作业时,只会用到 \(i-1\) 的状态,所以可以把状态优化为一维 \(f_{i,j} \Rightarrow f_j\) ,代码中表示为 \(f_i\) 。
// 滚动数组版本
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, res, a[N], f[N], sum;
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
sum += a[i];
}
for(int i = 1; i <= n; i ++)
{
for(int j = sum / 2; j >= a[i]; j --)
{
f[j] = max(f[j - a[i]] + a[i], f[j]);
}
}
for(int j = sum / 2; j >= 0; j --)
{
if(f[j])
{
res = f[j];
break;
}
}
cout << sum - res << '\n';
return 0;
}
// 非滚动数组版本
#include <iostream>
#include <algorithm>
#include <queue>
#include <set>
#include <map>
#include <vector>
#include <string>
#include <cstring>
#include <cmath>
#define fi first
#define se second
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const double eps = 1e-4;
const int N = 110, M = 1010;
ll f[N][M*N], n, a[N], sum;
void solve() {
scanf("%lld", &n);
for(int i=1; i<=n; i++) {
scanf("%lld", &a[i]);
sum += a[i];
}
for(int i=1; i<=n; i++) {
for(int j=a[i]; j<=sum/2; j++) {
f[i][j] = max(f[i-1][j], f[i-1][j-a[i]] + a[i]);
}
}
ll res = 0;
for(int i=1; i<=sum/2; i++) res = max(res, f[n][i]);
printf("%lld\n", sum - res);
}
int main() {
// multiple case
// int t; scanf("%d", &t);
// while(t--) {
// solve();
// }
// single case
solve();
return 0;
}
G(Ex).选队友
题目中对选队友有3个条件
- 选 \(m\) 个人
- 选到的每个人的能力值互不相同
- 任何两个人之间的能力差严格小于 \(m\)
以上3个条件 \(\Rightarrow\) 选择 \(m\) 个人,且他们的能力值为 \([x, x+m-1]\) 中的每一个整数。
假设 \(m=4\), 我们打算选 \(4\) 个能力值为 \(1(1), 2(3), 3(2), 4(2)\) ,括号中为有多少人的能力值相同。那么这样的选择方案(选能力值为 \(1,2,3,4\) 的方案)共有 \(1 \times 3 \times 2 \times 2 = 12\) 种。
故我们只需要将能力值预处理成这个能力值分别有几个人,然后循环遍历看是否符合条件即可。符合的话就算方案数。
为了不超时,我们需要在 \(O(1)\) 的复杂度内求得某种方案的方案数,可以采用前缀积来实现。注意的是因为结果会模 mod,所以这里的除法需要换成乘法逆元。
#include <iostream>
#include <algorithm>
#include <queue>
#include <set>
#include <map>
#include <vector>
#include <string>
#include <cstring>
#include <cmath>
#define fi first
#define se second
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const double eps = 1e-4;
const int N = 2e5+10, mod = 1e9+7;
int n, m, a[N];
pii b[N];
ll fact[N], exfact[N];
// 快速幂,这里是为了求逆元
ll qmi(ll a, ll b) {
ll res = 1;
while(b) {
if(b&1) res = res * a % mod;
b >>= 1;
a = a * a % mod;
}
return res;
}
void solve() {
scanf("%d%d", &n, &m);
for(int i=1; i<=n; i++) {
scanf("%d", &a[i]);
}
sort(a+1, a+1+n);
// 将能力值处理为 b[k] = {能力值, 人数}
int k=0;
for(int i=1; i<=n; i++) {
int j = i;
while(j <= n && a[i] == a[j]) j++;
b[++k] = {a[i], j-i};
i = j-1;
}
// 人数的前缀积 与 人数前缀积的逆元
fact[0] = 1;
exfact[0] = qmi(1, mod-2);
for(int i=1; i<=k; i++) {
fact[i] = fact[i-1] * b[i].se % mod;
exfact[i] = exfact[i-1] * qmi(b[i].se, mod-2) % mod;
}
ll res = 0;
for(int i=1; i+m-1<=k; i++) {
int j = i + m - 1;
if(b[j].fi - b[i].fi >= m) continue;
res = (res + fact[j] * exfact[i-1]) % mod;
}
printf("%lld\n", res);
}
int main() {
// multiple case
int t; scanf("%d", &t);
while(t--) {
solve();
}
// single case
// solve();
return 0;
}

