Educational Codeforces Round 113 (Rated for Div. 2) C. Jury Meeting 题解

题目

题目地址

Educational Codeforces Round 113 (Rated for Div. 2) C. Jury Meeting

题目大意

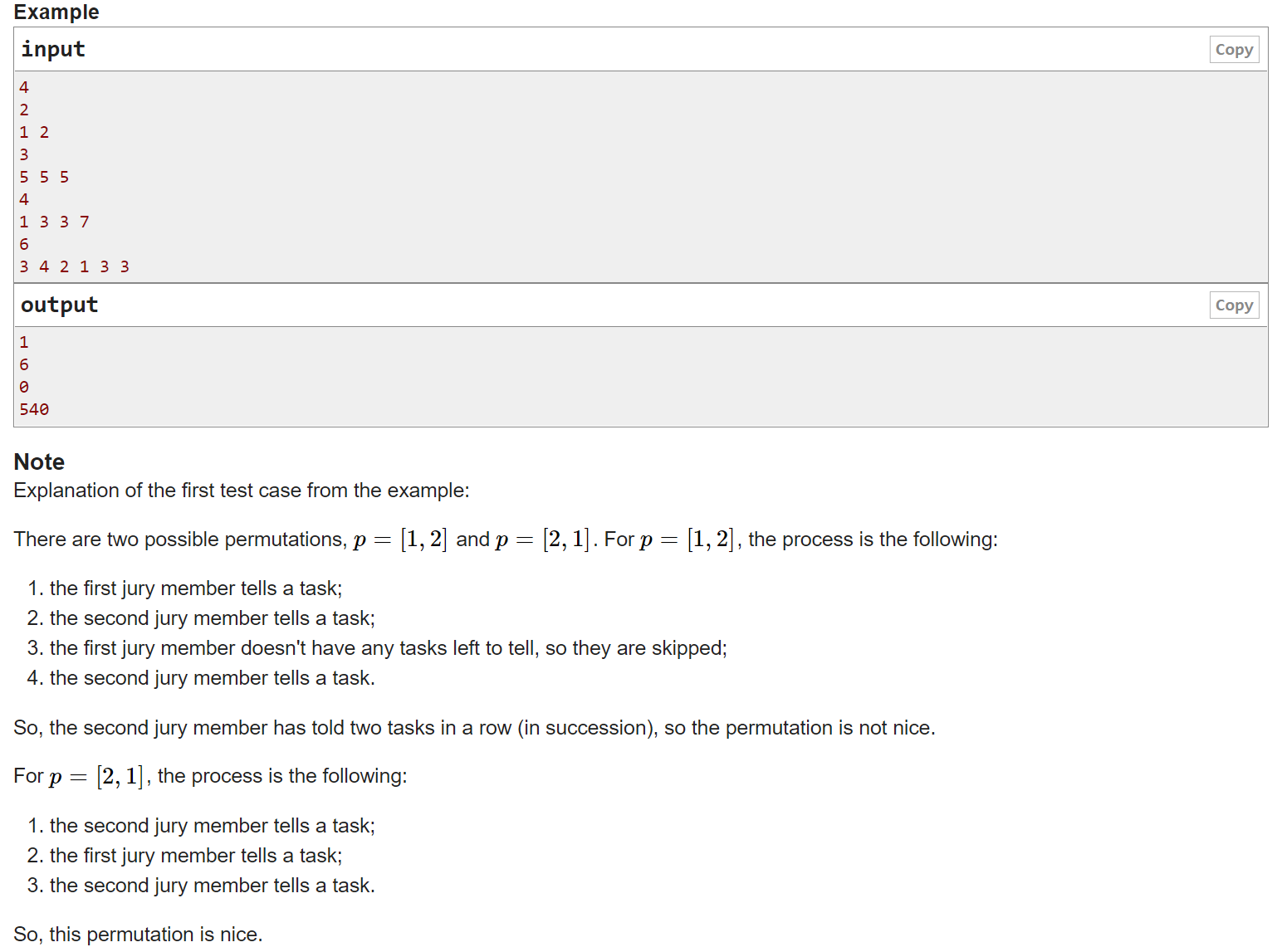
题目大意是说有\(n\)个人，第\(i\)个人有\(a_i\)个任务。
现在有一个排序，第\(j\)个数为\(i\)表示第\(i\)个人执行一个任务，即\(a_i = a_i - 1\)。一直按照这个排序循环下去，如果这个人没任务了就跳过。直到执行完所有任务为止。
假如执行过程中，没有出现同一个人连续执行2次任务的情况，那么就说明这个排序是\(nice\)的。现在求有多少种\(nice\)的排序。

输入样例

4
2
1 2
3
5 5 5
4
1 3 3 7
6
3 4 2 1 3 3

输出样例

1
6
0
540

题解

思路

简单模拟一下样例可以发现：

• 如果任务数最大为\(mx\)，且有2个人的任务数都是\(mx\)，那么无论何种顺序执行任务，都不会出现同一个人连续2次执行任务的情况。也就是任何排列都是nice的。这时情况数为\(n!\)
• 如果任务数最大为\(mx\)，而\(mx - 1\)没有的话，那么无论何种顺序执行任务，一定会出现任务数最多的那个人连续执行2次任务的情况。也就是此时没有排序是nice的。这时情况数为\(0\)

还剩下一种情况，就是任务数为\(mx\)的只有一个人，任务数为\(mx - 1\)的有\(k\)个人。只要这\(k\)个人中有个人在\(mx\)的后面执行任务，那么这个序列就一定是nice的。
可以先求出来bad的情况数，也就是\(k\)个人都在\(mx\)前面执行任务，最后总的减去就行。
首先除了最大值以及最大值-1的值外，还有\(n - k - 1\)个值，这些值有\(A_{n}^{n-k-1}=\frac{n!}{\left( k+1 \left) !\right. \right.}\)种排列方式。如果是bad排列，那么最大值一定在最后一位，其余\(k\)的排列方式为\(A_{k}^{k}= k!\)。故总共的bad排列的情况数为\(\frac{n!k!}{(k+1)!}\)即\(\frac{n!}{k+1}\)。 那么此时nice的情况数为\(n! - \frac{n!}{k+1}\)

代码

Then show the code.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef long long LL;
const int mod = 998244353;

int main(){
    int t, n;
    cin >> t;
    while(t--){
        cin >> n;
        vector<int> a(n);
        for(auto &x:a) cin >> x;
        auto mx = *max_element(a.begin(), a.end()); //找出最大值
        int mxn = count(a.begin(), a.end(), mx);
        int k = count(a.begin(), a.end(), mx-1);
        int res=1, sub=1;
        for(int i=1; i<=n; i++){
            res = (LL)res*i%mod;
            if(i!=k+1) sub = (LL)sub*i%mod;
        }
        if(mxn>=2) cout << res << endl;
        else if(!k) cout << 0 << endl;
        else cout << (res-sub+mod)%mod << endl; //防止结果为负数
    }
    return 0;
}