hash
概念
hash,也称散列,可以理解为一种思想:将复杂数据转换为一个标志,映射入简单值域中,用来方便存储与查询。
其实就像离散化可以将数字与其的大小顺序一一对应那样,不过离散化是提前预处理,先把所有目标数据获取后才能离散。
hash大多时候是使用散列函数直接计算,比如取模,这样可以保证同样的数据对应同样的标志,不过很难有逆向规律,同样标志不一定对应同样的数据,当发生不同信息被映射为相同值情况我们称为hash冲突。
解决一般情况冲突可以使用hash表。
hash表
建立一个邻接表,以函数值域为表头,把映射后hash值一样的数据先归为一类,插入一个节点可以保存原始值与统计信息。
比如我们如果要在序列中统计每个数出现了多少次,使用hash表来解决,对一个数求出hash值,然后找到该hash值对应的一类,在遍历这一类找到对应节点。
由于hash值可以通过取模等方式将原本有规律的数据变得更加随机,相当于把链表与数组计数的优点结合在了一起,所以数据的分布将会较为均匀,复杂度也比较优秀。
一般情况下,若取模的模数越大,复杂度就越可观,通常可以开到5056577(够大,同时比较好记),近似为O(1)。
#define ll unsigned long long
#define N1 10056577
using namespace std;
struct hash_table {
int head[N1], nex[N1], n1; ll num[N1], cnt[N1];
int mod=5056577;
int hash(ll x) {return x%mod+1;}
void add(ll x, int val) {
int y=hash(x);
for(int i=head[y];i;i=nex[i]) if(num[i]==x) {cnt[i]+=val; return;}
num[++n1]=x; nex[n1]=head[y], head[y]=n1; cnt[n1]=val;
}
int ask(ll x) {
int y=hash(x);
for(int i=head[y];i;i=nex[i]) {if(num[i]==x) return cnt[i];}
return 0;
}
} H;
字符串hash(序列hash)
取一固定值p,将字符串s视作p进制数,设hash值为\((s[n]*p^0+s[n-1]*p^1+…+s[1]*p^{n-1})\mod M\).
一般来说p可取131或13331,M=2^64(unsigned long long自然溢出),此时hash冲突概率极低,因此此时当hash值相同可以直接认为两串相同。
代码:
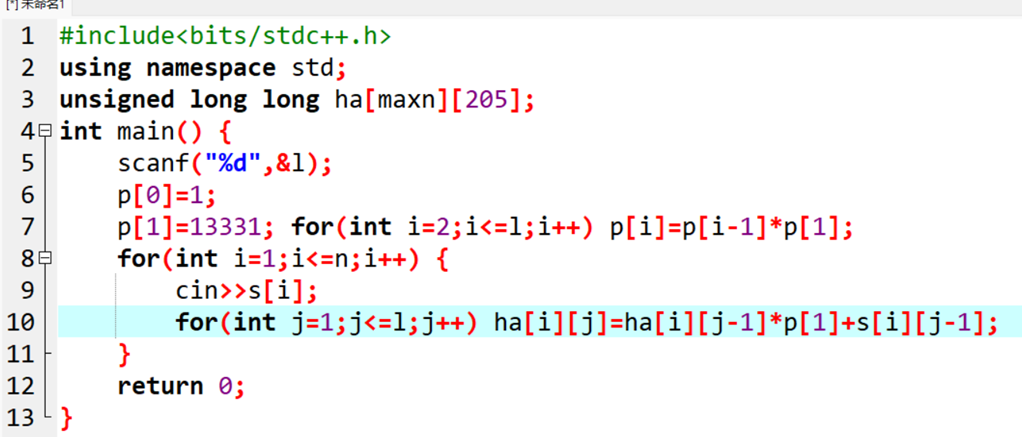
当把每一位的ha求出,对于这个字符串已经可以算出每个字串的hash值。
假如字串为\([l,r]\),那么字串hash值便是\(ha[r]-ha[l-1]*p^{r-l+1}\),相当于p进制下补0的方式补回位权,恰好抵消掉\([1,r]\)的前\([1,l-1]\)部分。
如一串abcde,想取\([4,5]\):de, 对应\(ha[5]\),其前缀abc对应\(ha[3]\):
\(ha[5]='a'*p^4+'b'* p^3+'c'* p^2+ 'd'* p^1+'e'* p^0\)
\(ha[3]='a'*p^2+'b'* p^1+'c'* p^0\), 则若把\(ha[3]*p^{5-3=2}\):
\(ha[3]' ='a'*p^4+'b'* p^3+'c'* p^2\),用\(ha[5]\)减去恰好为
\('d'* p^1+'e'* p^0=hash(de)\)。
这意味着只需要O(n)预处理所有前缀和hash值,便能O(1)查询任意子串的hash值。
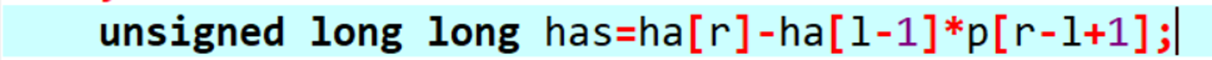
字符串比较(P4503企鹅 QQ )

对每个串,把它每一位分别变为空(权值为0)的情况hash值求出,最后进行统一比较。
下面以0表示空
如一个串为abcde,那求出“0bcde” , “a0cde” , “ab0de”, “abc0e” , “abcd0”的hash值,发现若有两个处理后的hash值相同,那对应的两个账户显然相似。
求出可以先求原串的hash值,接着按照位权减去即可。
如s[1]为'a',那最后\(hash(new)=ha[5]-'a'* p^{5-1}\)。
比较相同与否,其实可以将所有处理后的hash值全部提出来然后排序,逐位比较。
回文串(P3051 ANT-Antisymmetry)

判断回文串就是判一个串与其翻转后是否相同,用字符串hash可以预先在从左到右基础上再从右到左进行预处理,同理求出字串hash值,再去比较。
对于本题,在要求翻转基础上还要求反转,其实同理,在右到左处理时反过来0即可。
这题不可以暴力确定左右端点,不妨确定中轴与两边延长的长度,因为回文串从这个角度看是有单调性的,如同一个点可以延长3就一定能延长2,那么可以使用二分,优化后复杂度\(O(nlogn)\)
判循环节(P3538 OKR-A Horrible Poem)

归根结底还是字串的比较,给出结论,在\([l,r]\)中,如果\([l,r-len]=[l+len,r]\)那么\([l,l+len-1]\)就是一个循环节。
比对一下就可以了。
\(aabaabaabaab000000\)
\(000000aabaabaabaab\)
而这个性质可以使用hash\(O(1)\)判定。
线段树与hash (ABC331F Palindrome Query)

序列的Hash具有可合并的性质:
\(all.has=l.has * p^{r.len} + r.has\)
而这样的合并可以放到线段树内,在push_up内做点小更改即可:
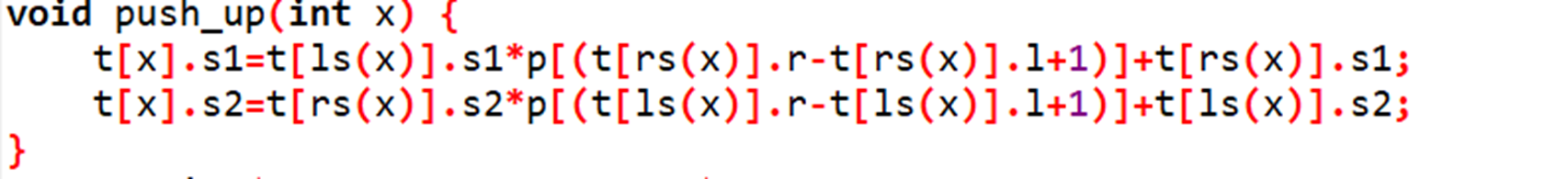
当序列修改时,线段树内的hash值便可以用O(logn)的复杂度维护,可以用于解决许多更改后的比较问题。
套入线段树内,线段树设定两个值,一个表示从前到后,一个表示从后到前。
分别按照两种方式合并与查询。
如果两个查询的值相等,那么它就是回文串。
树hash
一种把树的结构映射为数值的一般方式:设定以x点为根的子树的hash值为\(h[x]\),y为x的儿子,\(siz[x]\)表示以x为根的子树大小,\(pri[x]\)表示第x个质数,有以下转移式:
\(f[x]=1+\sum_{y\in{son~of~x}} f[y]* pri[siz[x]]\)
通过用质数的分散性把数据随机化,提高了正确率
在这种转移下,可以先一遍dfs遍历出所有的\(f[x]\),接着仿照换根dp思想把以各个点为根时整棵树的hash值全部求出,以此来表示一颗树所有可能的形态。
设\(g[x]\)为以x点为根的hash值,fa为x的父亲,那么换根式子为:
\(g[x]=(g[fa]-f[x]* pri[siz[x]]) * pri[all-siz[x]]+f[x]\)
树的比对(P4323 [JSOI2016] 独特的树叶)

先把A,B树以各个点为根的hash值全部遍历一遍求出,然后把B树的叶节点找出,如果要删去这个点,如有一叶节点x,可以看作以x的父亲fa为根整棵树的hash值减去h[x],注意一开始根节点有可能叶为叶子,这时hash值为其子节点x的h[x]。
求出hash值后一切皆不难去处理,可以整理后排序比较,也可以即时使用hash表,map,set等容器模拟数组计数。
和hash
有些时候判定的条件也许只满足必要性不满足充分性,但是我们又想运用比较快速的方式去解决,和hash也许会成为一种选择。
和hash就是把一些数据事先赋予随机的标志,通常为随机的权值,通过对这些权值进行操作后得到一个必要但不充分的答案,由于数据的随机性把它视作正确的。
虽然看着很悬,但实际上不充分也有很大的概率是正确的,如果再多准备好几组数据,错误率会大大降低。
P8819 [CSP-S 2022] 星战
题面翻译过来就是对一张图进行操作,也就是加边和删边而已,胜利条件简略一下就是问是否每一个点的出度都为1。
注意到操作都可以看做对一条边的终点进行操作,故出度其实不好维护,反倒是维护入度较为方便。
每一个点的出度都为1,相当于所有点的入度总和为n,于是所有度数之和是否为n就是一种必要但不充分的条件,但错误率太高了,考虑使用和hash优化。
可以给每一个点赋予一个随机的权值,维护对一个点来说所有进入它的点的权值之和f,如此一来,所有f的总和可以视作出度和一般,那么,当这个总和等于每个点的权值和时,视作判定正确。
由于多出了随机性,一个权值的作用没有那么好替代,故正确性提高,对CCF数据只用一组随机,当然保险起见多组结合更能保障正确性。
CF1746F Kazaee
n和q都是3e5级别。
出现次数都是k倍数这一点很难100%正确去维护,于是考虑找必要但不充分的条件。
可以看出,整个区间出现的次数总和应当是k的倍数,不过这样正确性太低了。
不妨如法炮制,给每一种数都赋予一个随机权值,当一个区间中的权值之和为k的倍数,那么必要性已经满足。
由于数据具有随机性,恰好错误的情况其实概率比较低,如k=2,完全可以将错误率看成1/2,
这时加上30组数据左右就可以把概率压至极小,完全可以视作正解。
例题整理
P8085 [COCI2011-2012#4] KRIPTOGRAM
为了让两串对应,可以设定一个对应序列表示之间距离的关系。
如aba,分别为0 0 2, abaab为0 0 2 1 3, 发现如果按同规则对应序列会完全一致。
但是对于第一个需要维护,但一个点只对应后面一个相应的点,只会影响一个点。
可以事先记录,实时维护。
P6688 可重集
发现问题查询比是较比较复杂,但操作简单,这时可以往hash去想。
一开始欲用区间平方和,但是往次方去考虑不仅难写,重要是它会被卡。
其实发现,支持一个序列集体+=k,不如对一位x,维护\(p^{a[x]}\),这样当集体加上k,只需要全部乘以\(p^k\)即可。
维护他们区间和,当两个区间和相等认为他们相同。
P3230 [HNOI2013] 比赛
考虑搜索,以每场比赛按照\((1,2),(1,3),..,(n-2,n),(n-1,n)\)的顺序作为步骤。
对每场比赛枚举情况,这样复杂度为\(O(3^{n^2})\),自然无法接受,所以需要剪枝。
这里有一个很重要的点,当一个人完赛后,比如按照顺序的3号比完\((3,n)\)这一场之后,后面的人\((4,5,...,n)\)还需要的分数成为了另外一个独立的子问题。
我们可以考虑对这样的子问题进行记忆化,方法就是把他们还需要的分数排序后使用hash记录这样的一组情况序列。
后面用map把hash值数组计数,若重复直接返回。
P5123 [USACO18DEC] Cowpatibility G
奶牛不能相处可以考虑容斥,把每头牛所有口味可能组合序列都给hash散列。
后面考虑每一种口味组合序列,这时可以直接找出有多少种相同hash值,认为相同hash值即相同序列。
发现成功取出了包含口味数量与符合要求牛数量,套入容斥即可。
P3763 [TJOI2017] DNA
询问s0串中有多少字串经过不大于3次修改可变为s1。
先枚举s0每一个长度为len(s1)的字串,至于找修改次数,可以通过二分:
二分序列前缀长度,若两方的hash值相同则不存在不同,向右继续,否则向左。
最后把最前面的不同点标记出来,后面查询hash值时额外计算这些标记点修正后的hash值即可。
这样的二分可以进行3次,若超出三次则报不可能。
发现其实题目完全可以拓展成k次,复杂度\(O(nlog_n* k^2)\)
P3237 [HNOI2014] 米特运输
意即对每一个节点都会有一个值val,
我们需要计算出每个节点新的值f[x]为从上到下儿子数的乘积在乘上val,最后判断最多多少点f[x]相同。
直接乘肯定数据过大,考虑使用hash相关思想,其实很简单,就是取模。
可以设置多个模数,全部相同才判定相同。
P3823 [NOI2017] 蚯蚓排队
序列合并,拆开,询问很多长为k的串一共存在次数。
突破点很明显,<=50的k,
只需要在合并和拆开时分别维护左边和右边50个就足以面对所有询问。
发现询问次数高达\(10^7\),所以需要用hash表
记录串存在,可以在字符串hash之后将hash值放入hash表内计数,查询同理。



