《数据结构与算法之美》笔记 03 | 复杂度分析(上):如何分析、统计算法的执行效率和资源消耗?
其实挺久之前试听过这门算法课,但当时很浮躁,就记得当时听完好像有点混乱没怎么理解。今儿个摆正心态集中精神学习,发现其实很简单。
把经典的三个问题套进今天的内容,复杂度分析是什么,为什么需要进行复杂度分析,怎么分析?
1、复杂度分析是什么?
复杂度分析分为时间复杂度分析和空间复杂度分析。时间复杂度分析就是分析代码执行效率,空间复杂度分析就是分析代码占用存储空间的情况。
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
2、为什么需要复杂度分析?
因为实现一个需求解决一个问题,代码实现多种多样,对于有限的计算机资源,总是期望代码占用更少空间,用户总是期待软件运行速度更快,等待时间更少。
这就需要能有方法可以对代码进行评估,以筛选出执行效率更高资源消耗更少的代码。
代码跑一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小,为什么还要进行分析呢?
因为测试结果依赖测试环境,测试结果收测试数据规模影响很大。我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法。
3、怎么分析?
使用大O复杂度表示法
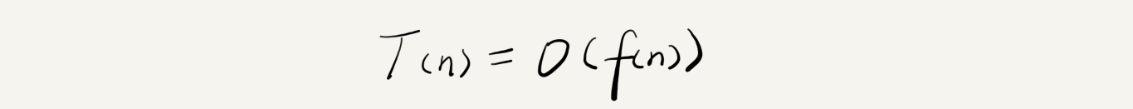
公式中的 O,表示代码的执行时间 T(n) 与 f(n) 表达式成正比。
忽略常数、系数和低阶
时间复杂度分析
- 只关注循环执行次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
![]()
对于刚罗列的复杂度量级,我们可以粗略地分为两类,多项式量级和非多项式量级。其中,非多项式量级只有两个:O(2n) 和 O(n!)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号