[LuoGu] P1004 方格取数
\(\color{red}{\mathcal{Description}}\)
设有 \(N \times N\) 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字 \(0\)。如下图所示:
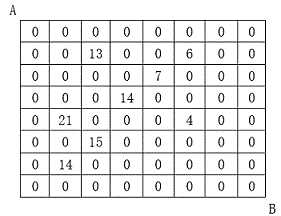
某人从图中的左上角 \(A\) 出发,可以向下行走,也可以向右行走,直到到达右下角的 \(B\) 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 \(0\) )。
此人从 \(A\) 点到 \(B\) 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
\(\color{red}{\mathcal{Input\ Format}}\)
输入的第一行为一个整数 \(N\)(表示 \(N \times N\) 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 \(0\) 表示输入结束。
\(\color{red}{\mathcal{Output\ Format}}\)
只需输出一个整数,表示 \(2\) 条路径上取得的最大的和。
\(\color{red}{\mathcal{DataSize\ Agreement}}\)
\(1 \leq N \leq 9\)
\(\color{red}{\mathcal{Solution}}\)
刚看到的时候感觉很简单,既然要求两条路径取得最大的和,那就跑两次 \(dp\) 不就好了,但这就是此题的坑人之处,因为下面这个图就是不行的
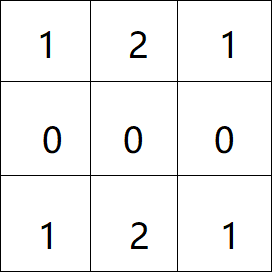
所以意识到,此题 \(dp\) 应该有同时性,也就是要同时进行
那么如何描述状态呢? 对于同时性开展的 \(dp\) ,有一点是必须知道的,就是步数
我们发现,对于走了 \(x\) 步得到的两个坐标 \((x_1,y_1)\) \((x_2,y_2)\) ,它们都在同一条对角线(自右上到左下)上,而对于在同一条对角线(自右上到左下)上的两点, 满足 \(x_1+y_1=x_2+y_2\)
这样一来就好做了,我们将步数,也就是对角线作为阶段,枚举两点的横坐标,就能算出它们各自的纵坐标
令 \(dp[k][i][j]\) 表示两点在 横纵坐标之和为 \(k\) 的这条对角线上,两点横坐标分别为 \(i\) 和 \(j\) 时能得到的最大的和,有如下状态转移方程
特别的,当两条路径到同一个方格的时候,应只取一次。
初始化(取决于个人) \(dp[2][1][1]=w[1][1]\)
\(\color{red}{\mathcal{Code}}\)
#include <bits/stdc++.h>
#define LL long long
#define reg register
using namespace std;
const int kN = 50;
int dp[kN][kN][kN];
int N, w[kN][kN];
int main() {
scanf("%d", &N);
int x, y, val;
while (1) {
scanf("%d%d", &x, &y);
if (!x && !y) break;
scanf("%d", &val);
w[x][y] = val;
}
dp[2][1][1] = w[1][1];
for (reg int k = 3; k <= N * 2; ++k) {
for (reg int i = 1; i < min(k, N + 1); ++i) {
for (reg int j = 1; j < min(k, N + 1); ++j) {
dp[k][i][j] = max(max(dp[k-1][i-1][j-1], dp[k-1][i][j-1]), max(dp[k-1][i-1][j], dp[k-1][i][j])) + w[i][k-i];
if (i != j) dp[k][i][j] += w[j][k-j];
}
}
}
printf("%d\n", dp[N * 2][N][N]);
return 0;
}
\(\color{red}{\mathcal{Source}}\)
\(NOIp\ 2000\ TG\ T4\)


